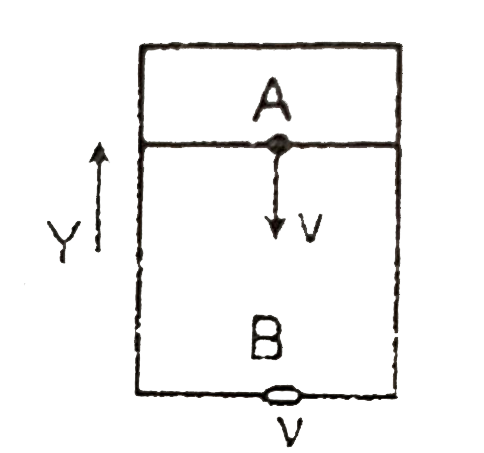
A container of cross-section area 'S' and height 'h' is filled with mercury up to the brim. Then the container is sealed airtight and a hole of small cross section area 'S/n' (where 'n' is a positive constant) is puched in its bottom. Find out the time interval upto which the mercury will come out from the bottom hole.
[Take the atmospheric pressure to be equal to h0 height of mercury column: h>h0]
The correct Answer is:14T∫0dt;t=n√2g(h−h0)
Let the velocity of effiux of mercury coming out of hole be v at an instant mercury level in container is y. aT same instant the speed of top surface of fluid v. From equilibrium of continuity
Snv=Sv….(1)
∵Sn<<S∴v>>v
applying Bernoulli's theorem between A and B
Yeg+12ev3=Patm+12ev2
∵v<<v higher powers of v can
be neglected and Patm=h0eg
∴v=√2g(Y−h0)......(2)
Hence mercury flows out of both till y=h0.
from equation (1)
v=−dydt=1hv=1h√2g(Y−h0)
or −dy√2gY−h0=1hdt
integrading between limits
at l=0y=n and t=T,Y=h0,−h0∫n−dy√2g(Y−h0)=1h=1nT∫0dt,t=n√2g(h−h0)
Related Playlists
Knowledge Check
- Question 1 - Select One
A tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)
Similar Questions
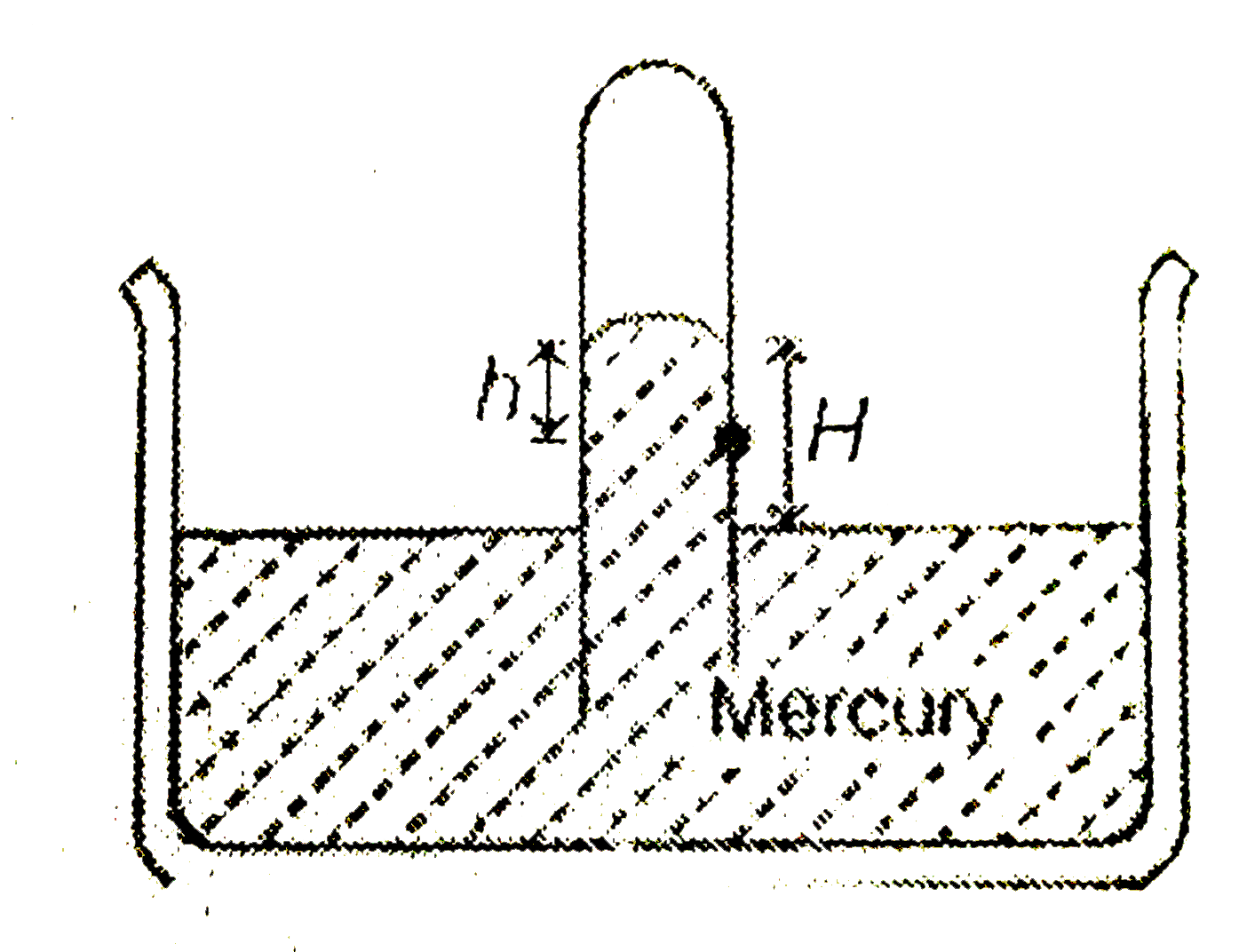
Consider the barometer shown in figure. Density of mercury is ρ. A small hole is made at point S as shown. The mercury come out from this hole with speed v equal to
 View Solution
View SolutionConsider the barometer shown in figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?
 View Solution
View SolutionThe vertical height of mercury in a simple barometer is dependant on the area of cross-section of barometer tube.
View SolutionA cylindrical container of radius 'R' and height 'h' is completely filled with a liquid. Two horizontal L-shaped pipes of small cross-sectional area 'a' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is
 View Solution
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 View Solution
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 View Solution
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA beaker of circular cross-section of radius 4 cm is filled with mercury up to a height of 10 cm. Find the force exerted by the mercury on the bottom of the beaker. The atmospheric pressure =105Nm−2. Density of mercury =13600kgm−3.Takeg10ms−2
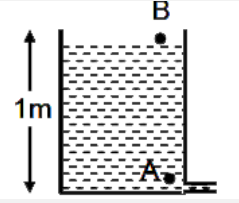
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
 View Solution
View Solution

