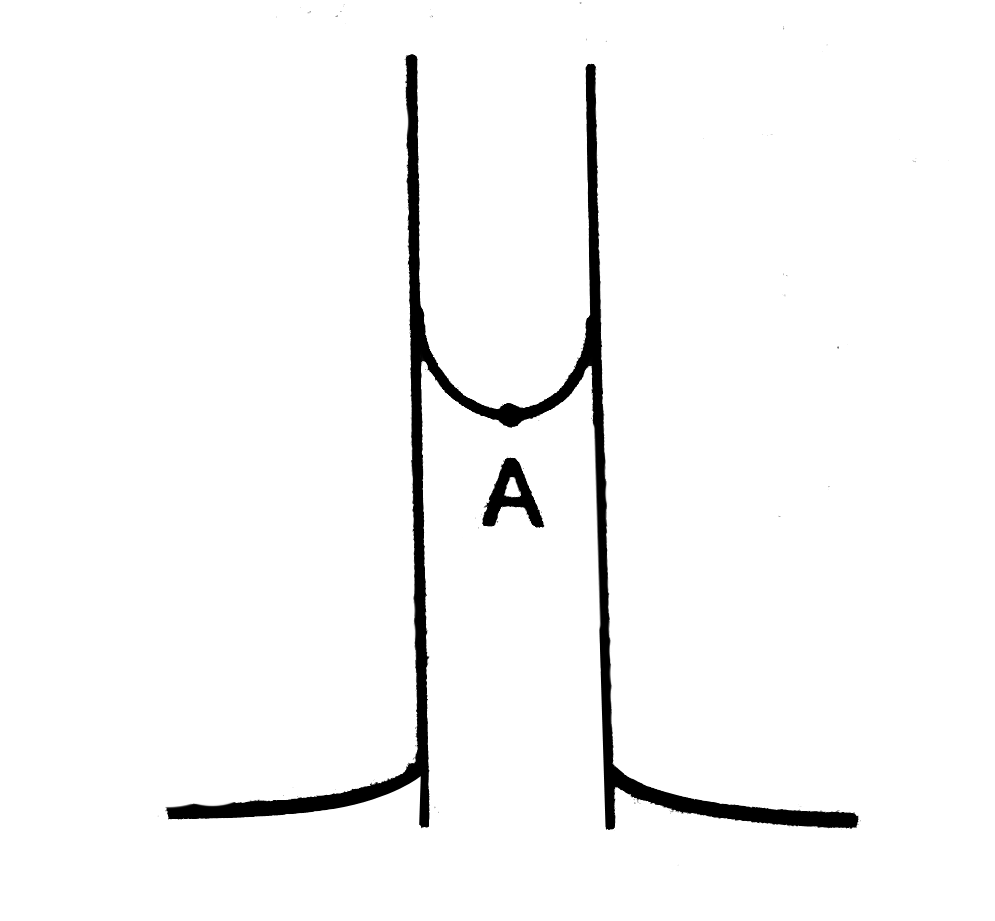Water is filled in a capillary tube of radius R. If the surface of water is hemispherical (θ=0), then find pressure at a point 'A' which is at h depth below the surface.

Water is on convex part. So pressure of water just below the surface will be less by 2TR. So pressure at point A is P02TR+pgh. Her surface of water was hemispherical (contact angle θ=0) so radius of curvature of the surface = radius of the tube =R.
Topper's Solved these Questions
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I
10 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
16 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
- UNITS, DIMENSION & MEASUREMENTBOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27 Videos
Similar Questions
Knowledge Check
In capillary pressure below the curved surface of water will be
AEqual to atmosphericBEqual to upper side pressureCMore than upper side pressureDLesser than upper side pressureWater rises to height h in capillary tube. If the length of capillary tube above the surface of water is made less than h then
Awater does not rise at all.Bwater rises up to the tip of capillary tube and then starts overflowing like a fountain.Cwater rises up to the top of capillary tube and stays there without overflowing.Dwater rises up to a point a little below the top and stays there.Water rises to a height fo 6 cm in a capillary tube of radius r. If the radius of the capillary tube is 3r, the height to which water will rise is ….cm.
A18B9C2D3
Water rises to height h in capillary tube. If the length of capillary tube above the surface of water is made less than h then
View SolutionIf 'M' is the mass of water that rises in a capillary tube of radius 'r', then mass of water which will ris in a capillary tube of radius '2r' is :
View SolutionA capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
View SolutionA capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
View SolutionWater rises to a height h in a capillary tube of radius r. The mass of water in the capillary tube is 10 g. The mass of water rising in another capillary tube of radius 4r will be
View Solution