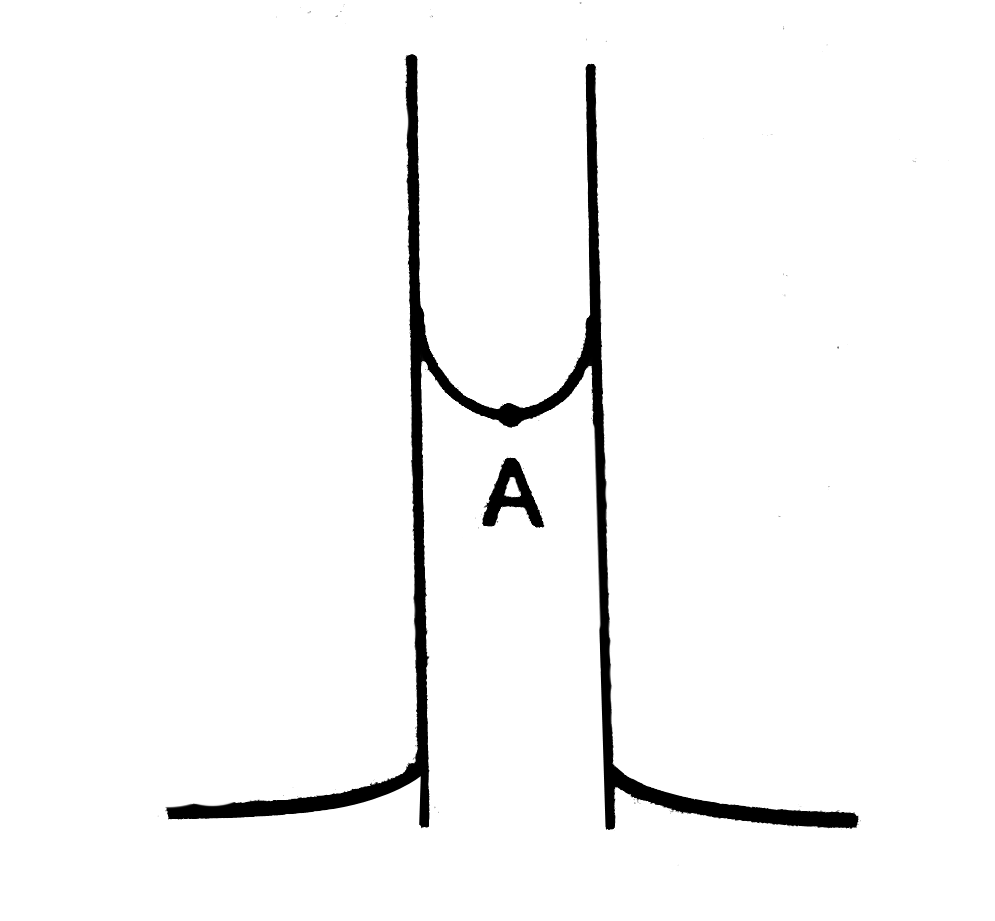Water is filled in a capillary tube of radius R. If the surface of water is hemispherical (θ=0), then find pressure at a point 'A' which is at h depth below the surface.

Draw normal (radial lines) at point A and B of periophery. The point (C) wherer radial lines meet is called centre of curvture. If contact angle is θ, from ΔACM,rC=Rsecθ
So radius of curvature of the surface rC=Rsecθ
Point to remember :
If the liquid surface is hemispherical (θ=0) then rc=R
If liquid surface is not hemispherical (θ≠0) then rc=Rsecθ

So pressure at A is P0−2TRsecθ+ρgh
Topper's Solved these Questions
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I
10 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
16 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
- UNITS, DIMENSION & MEASUREMENTBOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27 Videos
Similar Questions
Knowledge Check
If the surface tension of water is 0.06 N/m, then the capillary rise in a tube of diameter 1mm is (θ=0∘)
A1.22 cmB2.44 cmC3.12 cmD3.86 cmThe density of water at the surface of ocean is ρ . If the bulk modulus of water is B, then the density of ocean water at depth, when the pressure at a depth is αp0 and p0 is the atmospheric pressure is
AρKk−nP0BρKK+nP0CρKK−(n−1)P0DρK(K+(n−1)P0)
If the lower end of a capillary tube of radius 2.5 mm is dipped 8 cm below the surface of water in a beaker, then calculate the pressure within a bubble blown at its end in water, in excess of atompheric pressure. [Surface tension of water 72×10−3 N/m]
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionA capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
View SolutionIf 'M' is the mass of water that rises in a capillary tube of radius 'r', then mass of water which will ris in a capillary tube of radius '2r' is :
View SolutionThe excess pressure inside an air bubble of radius r just below the surface of water is P1. The excess pressure inside a drop of the same radius just outside the surface is P2. If T is surface tension then
View SolutionWater rises in a capillary tube to a height 4 cm. If the tube is inclined at an angle of 45∘ with the vertical , find the position of the water in the tube.
View Solution