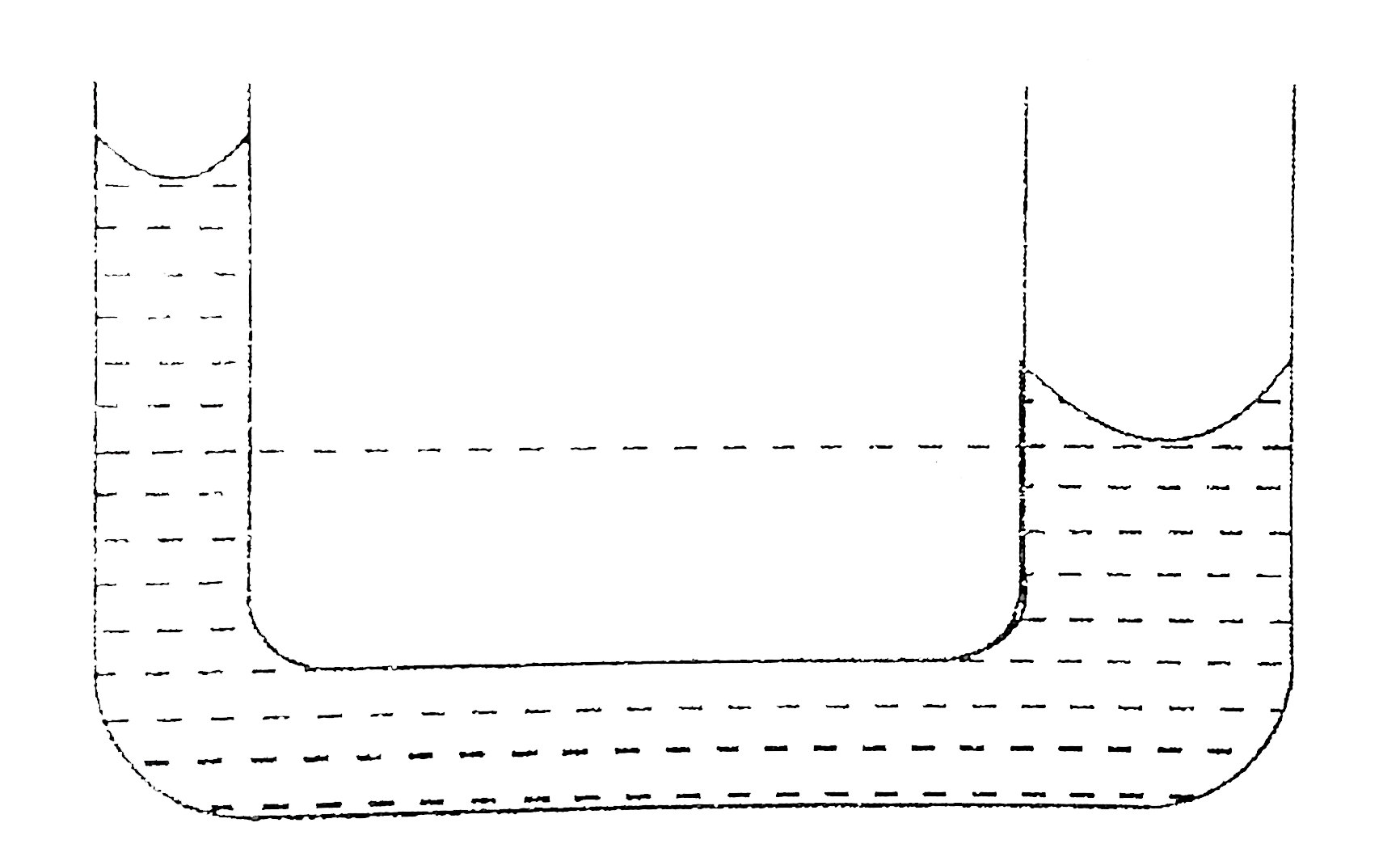
In the U−tube, radius of one arm is R and the other arm is 2R. Find the difference in water level if contact angle is θ=60∘ and surface tension of water is T.
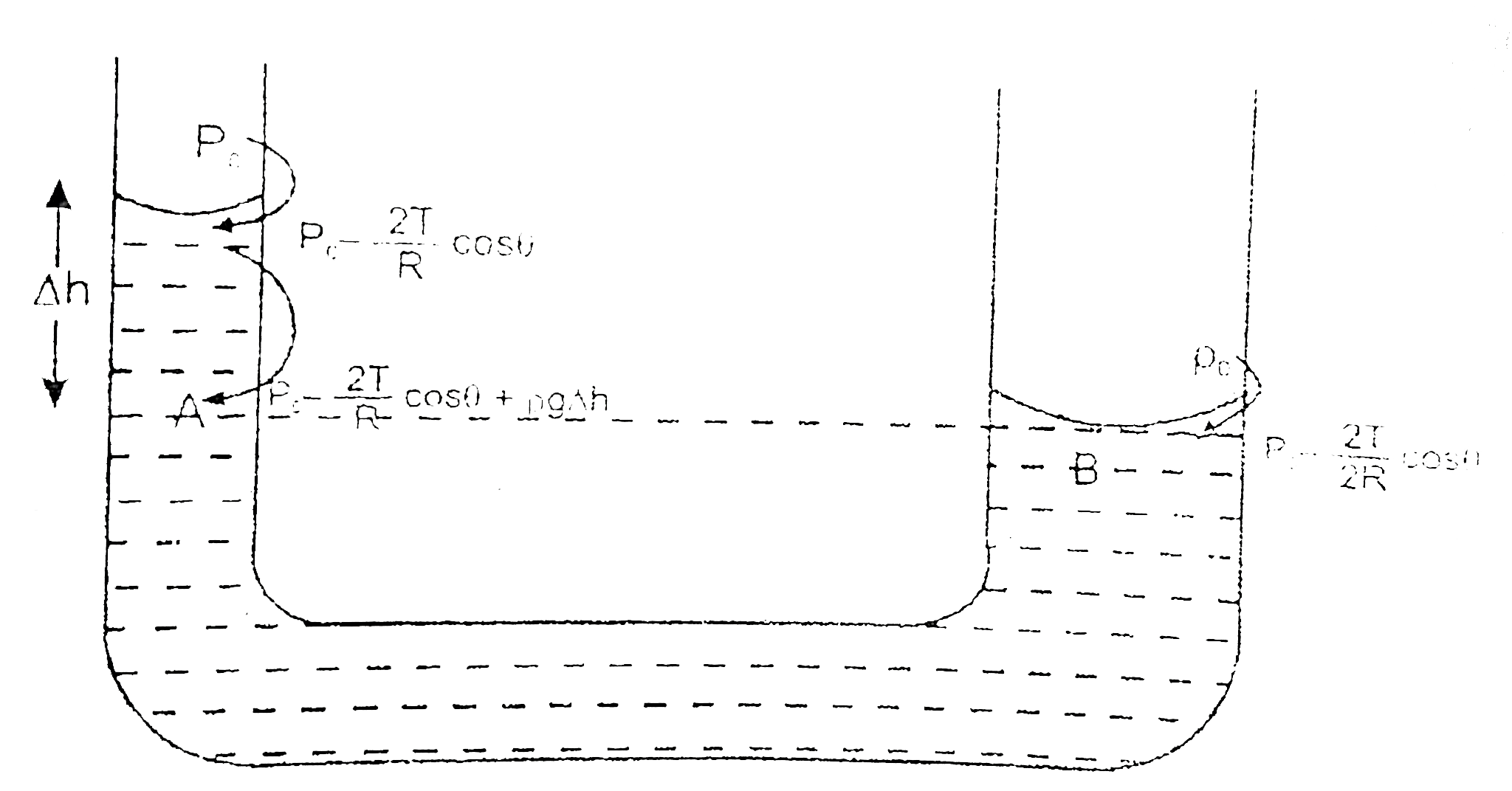
Balancing pressure at points A and B situated in same horizontal level.
P0−2TRcosθ+ρgΔh=P0−2T2Rcosθ
here θ=60∘, solving we get
Δh=T2ρgR
Topper's Solved these Questions
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I
10 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
16 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
- UNITS, DIMENSION & MEASUREMENTBOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27 Videos
Similar Questions
Two capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius R and left one has a radius of r(<R). The tube of radius R is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is θ=0∘. Let h be the height difference between water surface in the right and left tube. Surface tension of water is T and its density is ρ.
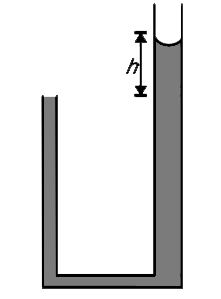
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .
View SolutionA glass U−tube is inverted with open ends of the straight limbs, of diameters 0.5mm and 1.0mm below the surface of water in a beaker. The air pressure in the upper part is increased until the meniscus in one limb is level with the water outside. Find the height (cm) of water in the other limb in nearest integer. : (Density of water is 103Kg/m3 and surface tension of water is 7.5×10−2N/m. Take contact angle θ=0∘)

View Solution
Knowledge Check
On heating water, bubbles beings formed at the bottom of the vessel detatch and rise. Take the bubbles to be spheres of radius R and amking a circular contact of radius r with the bottom of the vessel. If r<<R, and the surface tension of water is T, value of r just before bubles detatch is : (density of water is ρw)
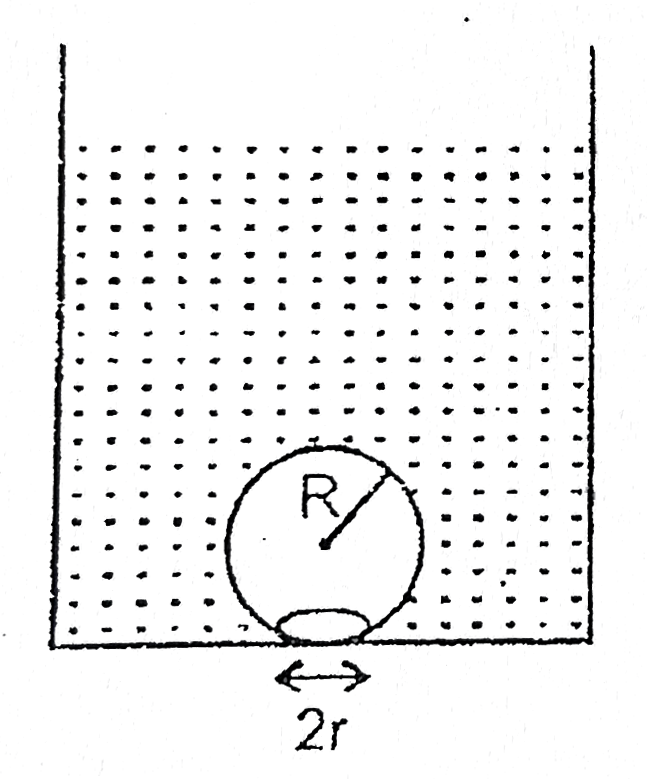 AR2√2ρmg3TBR2√ρag6TCR2√ρagTDR2√3ρagT
AR2√2ρmg3TBR2√ρag6TCR2√ρagTDR2√3ρagTOn heating water, bubbles beings formed at the bottom of the vessel detatch and rise. Take the bubbles to be spheres of radius R and amking a circular contact of radius r with the bottom of the vessel. If r<<R, and the surface tension of water is T, value of r just before bubles detatch is : (density of water is ρw)
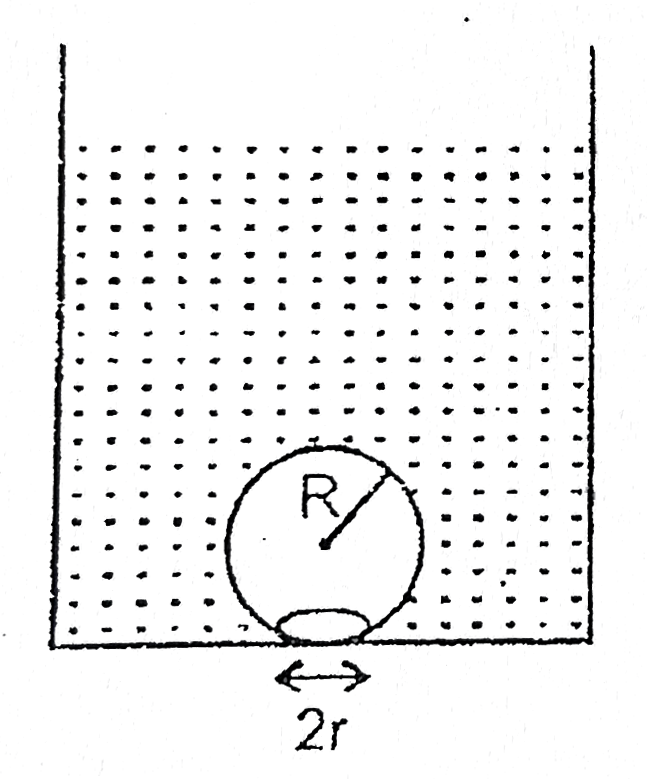 AR2√ρwg3TBR2√2ρwg3TCR2√ρwgTDR2√3ρWg3T
AR2√ρwg3TBR2√2ρwg3TCR2√ρwgTDR2√3ρWg3TThe two arms of a Verical U tube have internal radii of 0.4 cm and 0.8 cm respectively . The tube contains water . What is the difference in the surface levels of water in the two arms ? S.T of water =70×10−3 N/m
A0.7mmB1.785 mmC3.785 mmD5 mm
A narrow tube of length l and radius r is sealed at one end. Its open end is brought in contact with the surface of water while the tube is held vertical. The water rises to a height h in the tube. The contact angle of water with the tube wall is θ, density of water is ρ and the atmospheric pressure is Po. Find the surface tension of the liquid. Assume that the temperature of air inside the tube remains constant and the volume of the meniscus is negligible.
View SolutionA U tube is first partially filled with mercury. Then water is added in one arm and an oil is added in the other arm. Find the ratio of water and oil columns so that mercury level is same in both the arms of U tube. Given : Density of water =103kgm−3 , density of oil =900kgm−3.
View SolutionA glass rod of radius r1 is inserted symmetrically into a vertical capillary tube of radius r2 such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be (σ= surface tension of water, ρ= density of water)
View SolutionThe radii of two columns in a U tube are r1andr2(r1>r2). A liquid of density ρ is filled in it. The contact angle of the liquid with the tube wall is θ. If the surface tension of the liquid is T then plot the graph of the level difference (h) of the liquid in the two arms versus contact angle θ. Plot the graph for angle θ changing from 0∘→90∘. Assume the curved surface of meniscus to be part of a sphere.

View SolutionA glass rod of radius r1 is inserted symmetrically into a vertical capillary tube of radius r2 such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be (σ= surface tension of water, ρ= density of water)
View Solution
