Two parallel plates which are sparated by a very small distance d, are dipped in water. To how much height will the water raise between the plates (Assume contact angle θ→0)
Lets draw free body diagram of the water raised up. Forces on it are :
(i) The plates pull the surface in upward direction with a force 2Tl
(ii) The weight of raiseed water =(ρ)(lhd)g For equilibrium, force shoul be balanced.

2Tl=(ρ)(lhd)g⇒h=2Tρgd
Also Td/2=ρgh, so we can say that pressure excess due to cylindrical surface =Td/2=Trc
pressure excess due to spherical surface =2Tfc
pressure excess due to cylindrical surface =Trc
Alternative method :
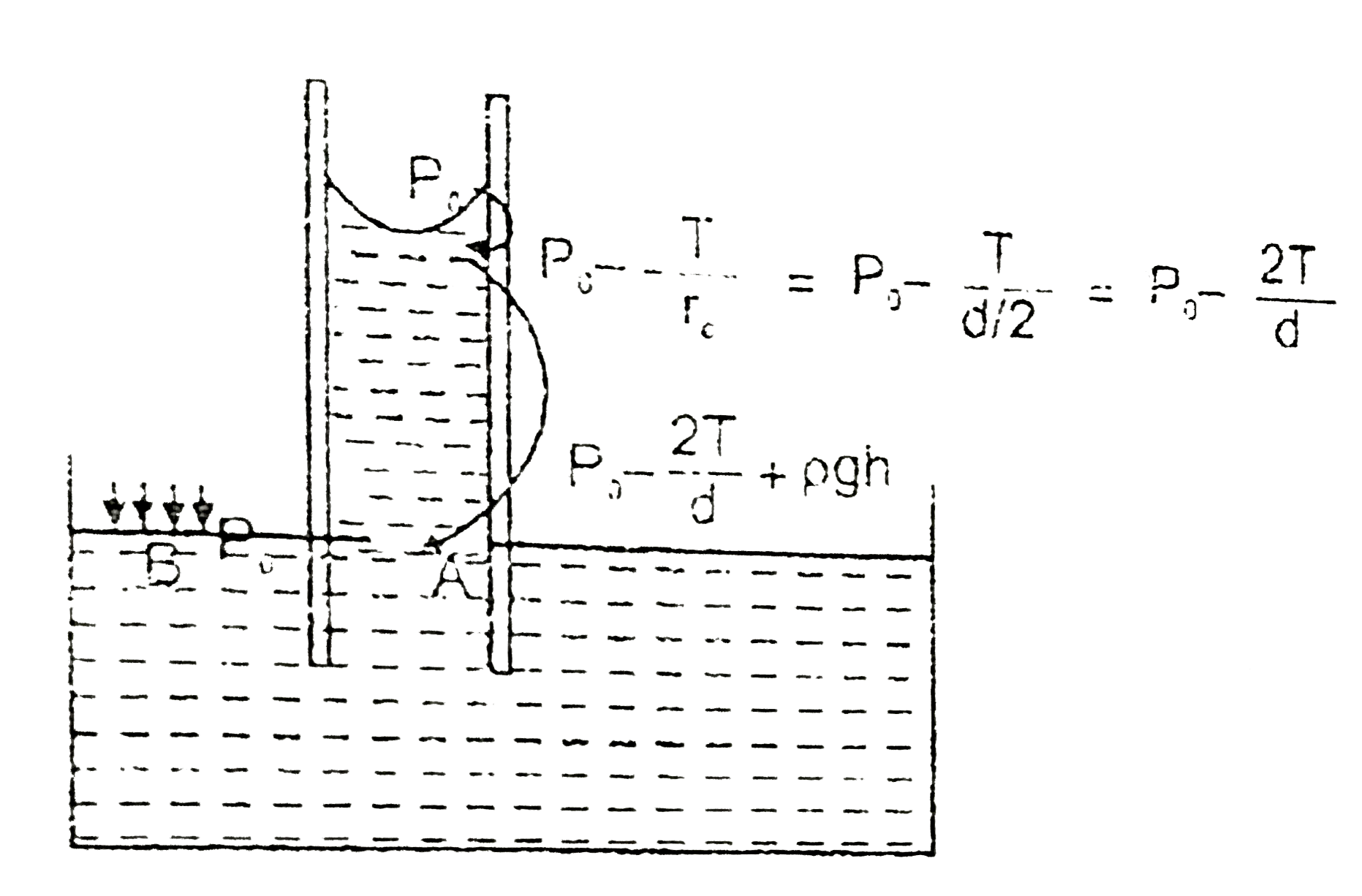
⇒P0−2Td+ρgh=P0⇒h=2Tρgd
Topper's Solved these Questions
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I
10 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
16 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
- UNITS, DIMENSION & MEASUREMENTBOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27 Videos
Similar Questions
A thin capillary of inner radius r1 and outer radius r2 (The inner tube is solid) is dipped in water. To how much height will the water raise in the tube ? (Assume contact angle θ→0)
View SolutionA thin capillary of inner radius r1 and outer radius r2 (The inner tube is solid) is dipped in water. To how much height will the water raise in the tube ? (Assume contact angle θ→0)
View Solution
Knowledge Check
Two vertical glass plates 1 mm apart are dipped into water. How high will the water rise between the plates. If the surface tension of water is 70 dyne cm−1
A1.43 cmB1.63 cmC2.86 cmD3.86 cm_E01_107_Q01.png)
Two very wide parallel glass plates are held vertically at a small separation d, and dipped in water. Some water climbs up in the gap between the plate. Let S be the surface tension of water P0= atmospheric pressure, P= pressure of water just below the water surface in the region between the plates-AP=P0−2SdBP=P0+2SdCP=P0−4SdDP=P0+4SdTwo parallel glass plates separated by a small distance x ar dipped partly in a liquid of density ' d keeping them vertical .The surface tension of the liquid is T and angle of contact is θ . What is the rise of the liquid between the plates due to capillarity ?
A2TcosθxdgB2TxdgcosθCTcosθxdgDTcosθxd
Two vertical glass plates 1 mm apart are dipped into water. How high will the water rise between the plates. If the surface tension of water is 70 dyne cm−1
View Solution_E01_107_Q01.png)
Two very wide parallel glass plates are held vertically at a small separation d, and dipped in water. Some water climbs up in the gap between the plate. Let S be the surface tension of water P0= atmospheric pressure, P= pressure of water just below the water surface in the region between the plates-
View SolutionTwo vertical parallel glass plates are partially submerged in water. The distance between the plates is d and the length is l. Assume that the water between the plates does not reach the upper edges of the plates and the plates and the wetting is complete. The water will rise to height (ρ= density of water and α= surface tension of water)
View SolutionTwo vertical parallel glass plates are partially submerged in water. The distance between the plates is d and the length is l. Assume that the water between the plates does not reach the upper edges of the plates and the wetting is complete. The water will rise to height (ρ= density of water and α= surface tension of water)
View SolutionTwo parallel glass plates are dipped partly in the liquid of denstiy 'd' keeping them vertical. If the distance between the plates is 'x', Surface tension is T and angle of contact is θ then ries of liquid between the plates due to capillary will be
View Solution
