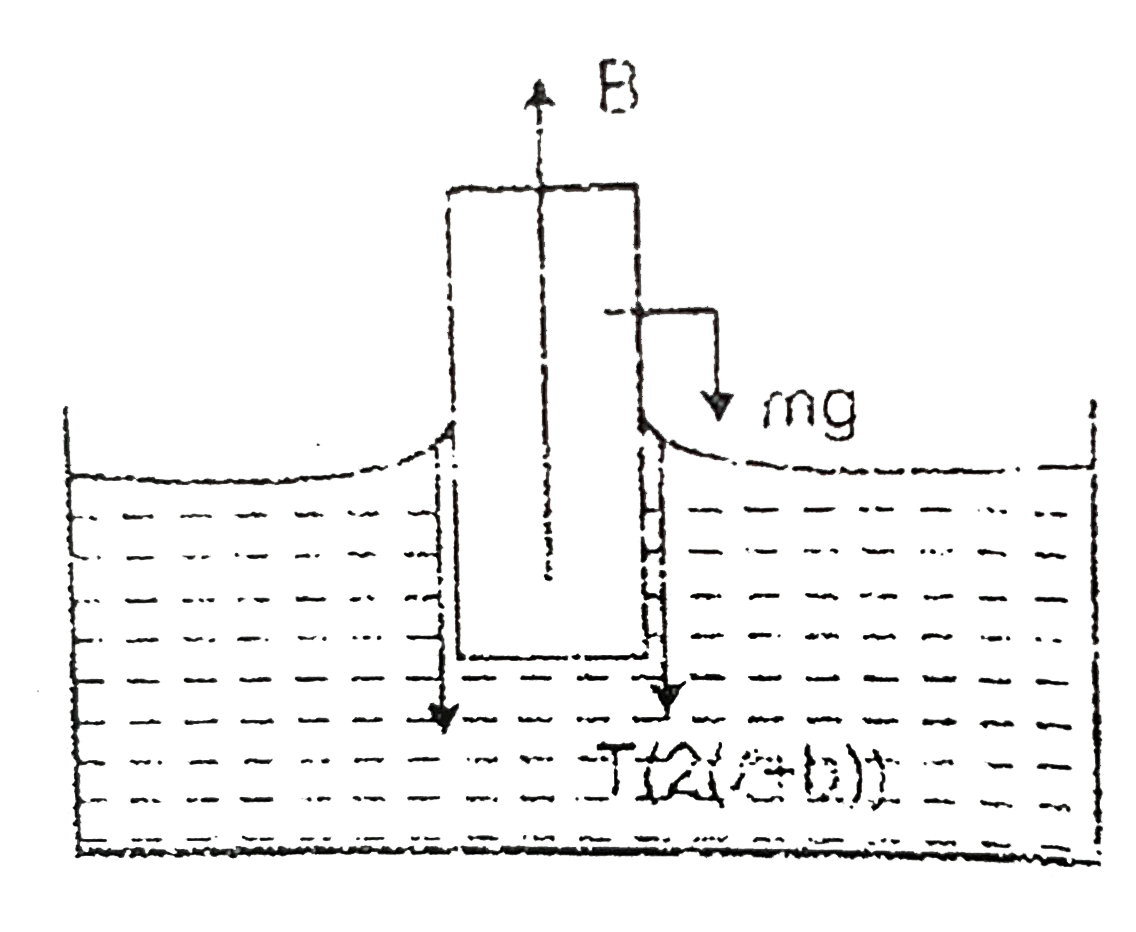
A glass plate of length 10cm, breath 1.54cmand thickness 0.20cm weigh 8.2gm in air. It is held vertically with the long side horizontal and the lower half under water. Find the apperent weight of the plate. Surface tension of water =73 dyne per cm, g=980cm/sec2.
The force acting on the plate are
(i) Buoyancive force of water acting upward
B=ρ1VSubg=1×1.54×10×0.22×980=1509.2dyne.
(ii) Weight of the system acting downward
=(8.2)×980dyne
(iii) Force of surface tension acting downward
=2(l×b)T=2(10+0.2)73=1489.2
So net downward force =mg+ (surface tension force) −B=(8.2)×980+1489.2−1509.2=8016.008dyne=8.1786gm force
Topper's Solved these Questions
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I
10 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
16 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
- UNITS, DIMENSION & MEASUREMENTBOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27 Videos
Similar Questions
A glass plate of length 10cm, breadth 1.54cm and thickness 0.20cm weigh 8.2g in air. It is held vertically with the long side horizontal and the lower half under water. Find the apparent weight of the plate. Surface tension of water =7.3×10−2N/m and =9.8ms−12
View SolutionA square glass plate of length 10 cm and thickness 0.4 cm, weight 40 g in air. It is held vertically such that its lower edge rests on water surface. What is the apparent weight of glass plate now? (Given surface tension of water = 0.073 N m−1)
View SolutionA glass plate of length 0.1m, breadth 15×103m and thickness 2×10−3m weighs 8×10−3kg in air, it is held vertically with its longer side horizontal and its lower half immersed in water. If the surfaces tension of water is 72×10−3N/m, the apparent weight of the plate is 79.4λ×10−3N. Then find λ
View SolutionTwo vertical glass plates 1 mm apart are dipped into water. How high will the water rise between the plates. If the surface tension of water is 70 dyne cm−1
View SolutionA wire of mass 1g is kept horizontally on the surface of water. The length of the wire that does not break the surface film is (surface tension of water is 70dy≠cm−1)
View SolutionThe force required to lift a circular flat plate of radius 5 cm on the surface of water is: (Surface tension of water is 75 dyne/cm):-
View SolutionA 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water =0.076Nm−1
View SolutionFind the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water =0.075Jm−2.
View SolutionA long capillary tube of radius r=1mm open at both ends is filled with water and placed vertically. What will be the height (in cm) of the column of water left in the capillary walls is negligible. (surface tension of water is 72dyne/cm and g=1000cm/sec2)
View SolutionA tube of conical bore is dipped into water with apex upwards. The length of the tube is 20cm and radii at the upper and lower ends are 0.1 and 0.3 cm. Find the height to which the liquid rises in the tube ( Surface tension of water = 80 dyne / cm ).
View Solution
