A soap bubble of radius r1 is placed on another soap bubble of radius r2(r1<r2). The radius R of the soapy film separating the two bubbles is :
r1+r2
√r21+r22
(r31+r32)
r2r1r2−r1
The correct Answer is:D
Equating pressures on the shaded portion :
4σr1−4σr2=4σR get R=r2r1r2−r1
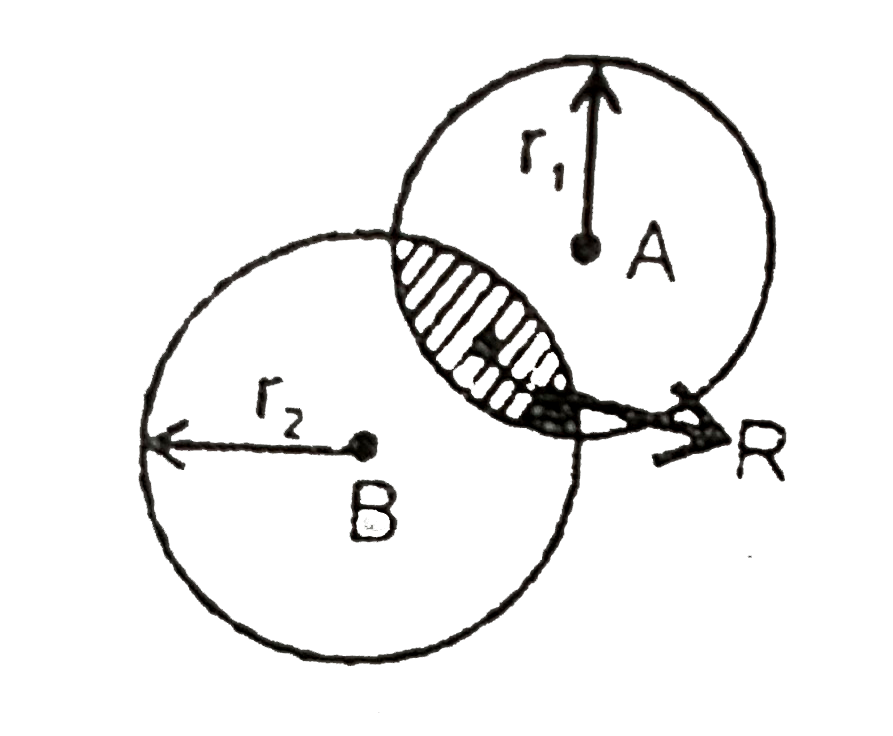
Topper's Solved these Questions
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 2 PART - II
12 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 2 PART - III
2 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
16 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
- UNITS, DIMENSION & MEASUREMENTBOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27 Videos
Similar Questions
Knowledge Check
A soap bubble of radius r is placed on another bubble of radius 2r. The radius of the surface common to both the bubbles is
A2r3B3rC2rDrProve that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
Ar2−r1Br2−r1r1r2Cr1r2r2−r1Dr2+r1A soap bubble of raidus R is surrounded by another soap bubble of radius 2R, as shown. Take surface tension =S. Then the pressure inside the smaller soap bubble, in excess of the atmosphere presure will be
 A4S/RB3S/RC6S/RDnone of these
A4S/RB3S/RC6S/RDnone of these
A soap bubble of radius r is formed inside another soap bubble of radius R(>r). The atmospheric pressure is P0 and surface tension of the soap solution is T. Calculate change in radius of the smaller bubble if the outer bubble bursts. Assume that the excess pressure inside a bubble is small compared to P0.
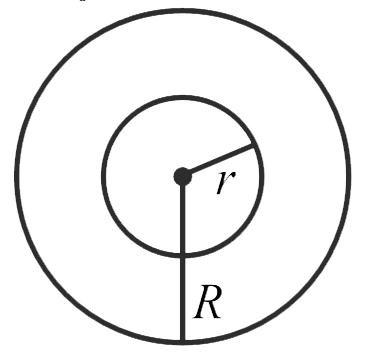
View SolutionA soap bubble of raidus R is surrounded by another soap bubble of radius 2R, as shown. Take surface tension =S. Then the pressure inside the smaller soap bubble, in excess of the atmosphere presure will be

View SolutionA soap - bubble with a radius 'r' is placed on another bubbles with a radius R (figure). Angles between the film at the point of contact will be -

View SolutionTwo soap bubbles coalesce.It noticed that, whilst joined together, the radii of the two bubbles are a and b where a>b.Then the radius of curvature of interface between the two bubbles will be
View SolutionA soap - bubble with a radius 'r' is placed on another bubbles with a radius R (figure). Angles between the film at the point of contact will be -

View Solution

