A 50kg motor rests on four cylindrical rubber blocks. Each block has a height of 4cm and a cross-sectional area of 16cm2. The shear modulus of rubber is 2×106N/m2. A sideways force of 500N is applied to the motor. The distance that the motor moves sideways is
0.156cm
1.156cm
0.312cm
0.204cm
The correct Answer is:A
To solve the problem, we need to calculate the sideways displacement of the motor when a force is applied to it. We will use the relationship between shear stress, shear strain, and the shear modulus.
1. Identify the Given Values:
- Mass of the motor (m) = 50 kg
- Height of each rubber block (h) = 4 cm = 0.04 m (convert to meters)
- Cross-sectional area of each block (A) = 16 cm² = 16 × 10⁻⁴ m² (convert to square meters)
- Shear modulus of rubber (η) = 2 × 10⁶ N/m²
- Applied sideways force (F) = 500 N
2. Calculate the Total Cross-Sectional Area:
Since there are 4 blocks, the total cross-sectional area (A_total) is:
Atotal=4×A=4×16×10−4m2=64×10−4m2=6.4×10−3m2
3. Calculate the Shear Stress (τ):
Shear stress is given by the formula:
τ=FAtotal
Substituting the values:
τ=500N6.4×10−3m2=78125N/m2
4. Relate Shear Stress to Shear Strain:
The relationship between shear stress and shear strain is given by:
τ=η⋅Xh
Where:
- X is the displacement (shear strain),
- h is the height of the rubber block.
5. Rearranging for X:
Rearranging the equation to solve for X:
X=τ⋅hη
Substituting the values:
X=78125N/m2⋅0.04m2×106N/m2
6. Calculating X:
X=31252000000=0.0015625m=0.15625cm
7. Final Result:
The distance that the motor moves sideways is approximately:
X≈0.156cm
Summary:
The sideways displacement of the motor when a force of 500 N is applied is approximately 0.156 cm.
- Mass of the motor (m) = 50 kg
- Height of each rubber block (h) = 4 cm = 0.04 m (convert to meters)
- Cross-sectional area of each block (A) = 16 cm² = 16 × 10⁻⁴ m² (convert to square meters)
- Shear modulus of rubber (η) = 2 × 10⁶ N/m²
- Applied sideways force (F) = 500 N
Since there are 4 blocks, the total cross-sectional area (A_total) is:
Atotal=4×A=4×16×10−4m2=64×10−4m2=6.4×10−3m2
Shear stress is given by the formula:
τ=FAtotal
Substituting the values:
τ=500N6.4×10−3m2=78125N/m2
The relationship between shear stress and shear strain is given by:
τ=η⋅Xh
Where:
- X is the displacement (shear strain),
- h is the height of the rubber block.
Rearranging the equation to solve for X:
X=τ⋅hη
Substituting the values:
X=78125N/m2⋅0.04m2×106N/m2
X=31252000000=0.0015625m=0.15625cm
The distance that the motor moves sideways is approximately:
X≈0.156cm
The sideways displacement of the motor when a force of 500 N is applied is approximately 0.156 cm.
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - II
6 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - III
8 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 1 PART - II
14 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
43 Videos
Similar Questions
The length of a rod is 20cm and area of cross-section 2cm2. The Young's modulus of the material of wire is 1.4×1011N/m2. If the rod is compressed by 5kg−wt along its length, then increase in the energy of the rod in joules will be
View SolutionA load of 100 N acts on a bar of length 10 cm and area of cross section 1 cm. Find the energy stored in it. (Y=1011N/m2)
View Solution
Knowledge Check
The area of a cross-section of steel wire is 0.1cm−2 and Young's modulus of steel is 2x1011Nm−2. The force required to stretch by 0.1% of its length is
A1000 NB2000 NCÂ 4000 ND5000N
Calculate the force required to incrase the length of wire of cross-sectional area 10−6m2 by 50% if the Young's modulus of the material of the wire is 90×109Pa.
View SolutionYoung's modulus of rubber is 104N/m2 and area of cross section is 2cm2. If force of 2×105dyn is applied along its length, then its final length becomes
View SolutionA uniform bar of length 2 m and cross-sectional area 50cm2 is subjected to a tensile load 100 N. If Young's modulus of material of bar is 2×107N/m2 and poisson's ratio is 0.4, then determine the volumetric strain.
View SolutionFor a toroid N = 500, radius = 40 cm, and area of cross section =10cm2. Find inductance
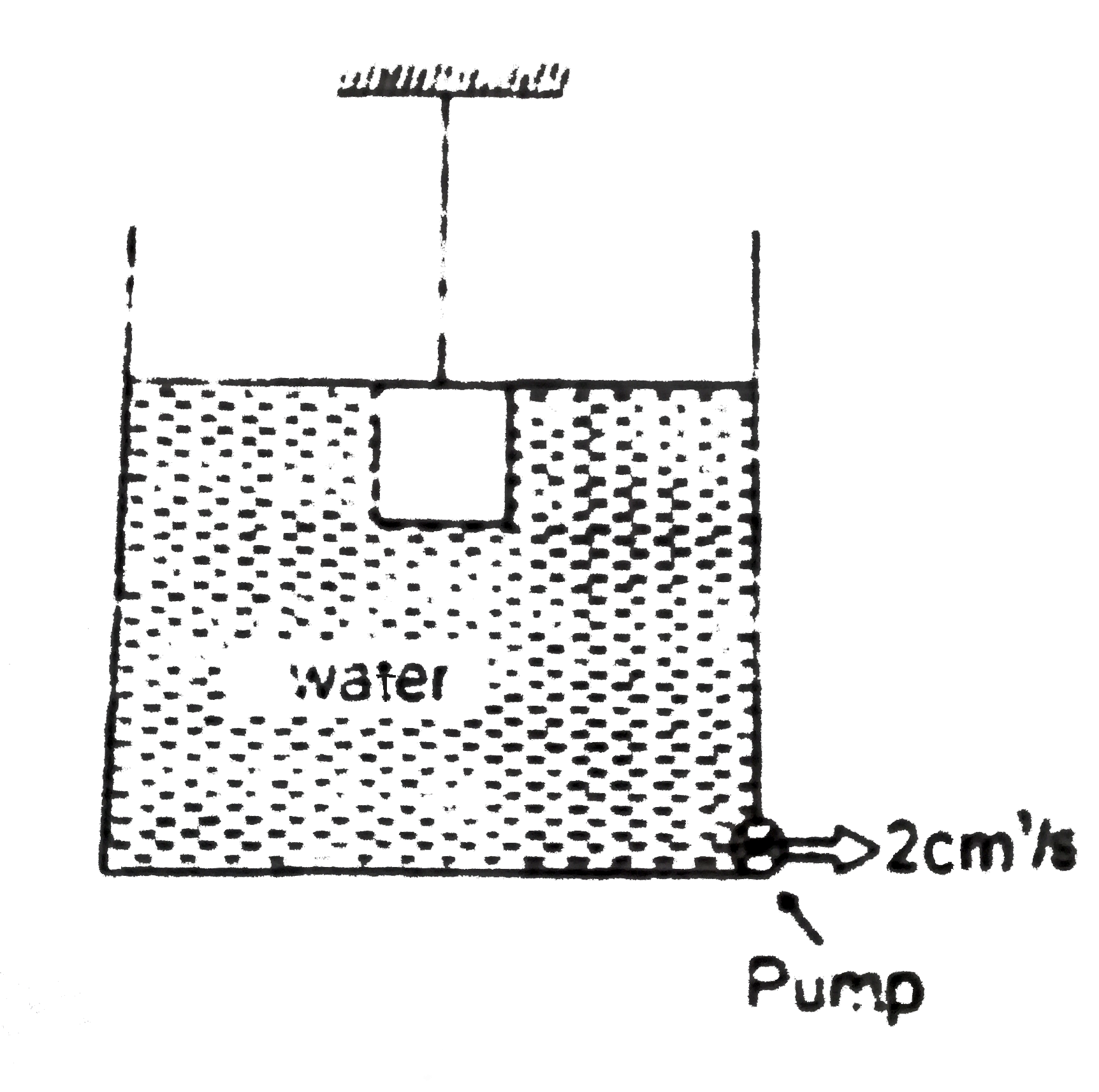
View SolutionFigure shows a cubical block of side 10 cm and relative density 1.5 suspended by a wire of cross sectional area 10−6m2. The breaking stress of the wire is 7×106N/m2. The block is placed in a beaker of base area 200cm2 and initially i.e. at t = 0, the top surface of water & the block coincide. There is a pump at the bottom corner which ejects 2cm3 of water per sec. Find the time at which the wire will break.
View SolutionWhat force is required to stretch a steel wire to double its length when its area of cross section 1 cm2 and Young.s modulus 2×1011N/m2.
View SolutionA uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View Solution
