Discuss the conditions for having
(a) interference , (b) maxima and minima.
To discuss the conditions for interference, maxima, and minima, we can break down the solution into clear steps:
Step 1: Understanding Interference
Interference occurs when two or more waves travel through the same medium and arrive at a point simultaneously. Each wave contributes to the overall displacement at that point, and the resultant displacement is the vector sum of the individual displacements.
Step 2: Types of Interference
There are two types of interference based on the phase relationship between the waves:
- Constructive Interference: This occurs when the waves are in phase (i.e., their crests and troughs align). The resultant intensity increases.
- Destructive Interference: This occurs when the waves are out of phase (i.e., the crest of one wave aligns with the trough of another). The resultant intensity decreases.
Step 3: Conditions for Maxima
For constructive interference (maxima), the path difference between the interfering waves must be an even multiple of half the wavelength (λ/2). Mathematically, this can be expressed as:
- Path difference = nλ, where n is an integer (0, 1, 2, ...).
Step 4: Conditions for Minima
For destructive interference (minima), the path difference must be an odd multiple of half the wavelength. This can be expressed as:
- Path difference = (n + 0.5)λ, where n is an integer (0, 1, 2, ...).
Step 5: Phase Difference for Maxima and Minima
The phase difference (Δφ) also plays a crucial role:
- For maxima (constructive interference), the phase difference must be an even multiple of π radians:
- Δφ = 2nπ, where n is an integer.
- For minima (destructive interference), the phase difference must be an odd multiple of π radians:
- Δφ = (2n + 1)π, where n is an integer.
Summary
In summary, interference occurs when waves superimpose, leading to constructive or destructive interference based on their phase relationship. The conditions for maxima and minima depend on the path difference and phase difference of the waves.
---
Interference occurs when two or more waves travel through the same medium and arrive at a point simultaneously. Each wave contributes to the overall displacement at that point, and the resultant displacement is the vector sum of the individual displacements.
There are two types of interference based on the phase relationship between the waves:
- Constructive Interference: This occurs when the waves are in phase (i.e., their crests and troughs align). The resultant intensity increases.
- Destructive Interference: This occurs when the waves are out of phase (i.e., the crest of one wave aligns with the trough of another). The resultant intensity decreases.
For constructive interference (maxima), the path difference between the interfering waves must be an even multiple of half the wavelength (λ/2). Mathematically, this can be expressed as:
- Path difference = nλ, where n is an integer (0, 1, 2, ...).
For destructive interference (minima), the path difference must be an odd multiple of half the wavelength. This can be expressed as:
- Path difference = (n + 0.5)λ, where n is an integer (0, 1, 2, ...).
The phase difference (Δφ) also plays a crucial role:
- For maxima (constructive interference), the phase difference must be an even multiple of π radians:
- Δφ = 2nπ, where n is an integer.
- For minima (destructive interference), the phase difference must be an odd multiple of π radians:
- Δφ = (2n + 1)π, where n is an integer.
In summary, interference occurs when waves superimpose, leading to constructive or destructive interference based on their phase relationship. The conditions for maxima and minima depend on the path difference and phase difference of the waves.
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - I
34 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - II
30 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Solved Examples
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
What are the conditions for sound to interfere ?
View SolutionList the conditions necessary for sustained interference.
View SolutionDefine interference. List the conditions of obtaining sustained interference.
View SolutionState one condition for obtaining a sustained interference of light.
View SolutionState the necessary conditions for the interference of two sound waves.
View SolutionThe ratio of intensities of two waves is 2. the ratio of intensities of maxima and minima when these waves interfere is approximately
View SolutionWhen a plane wave front of light, of wavelength λ, is incident on a narrow slit, an intensity distribution pattern, of the form shown is observed on a screen, suitably kept behind the slit. Name the phenomenon observed.
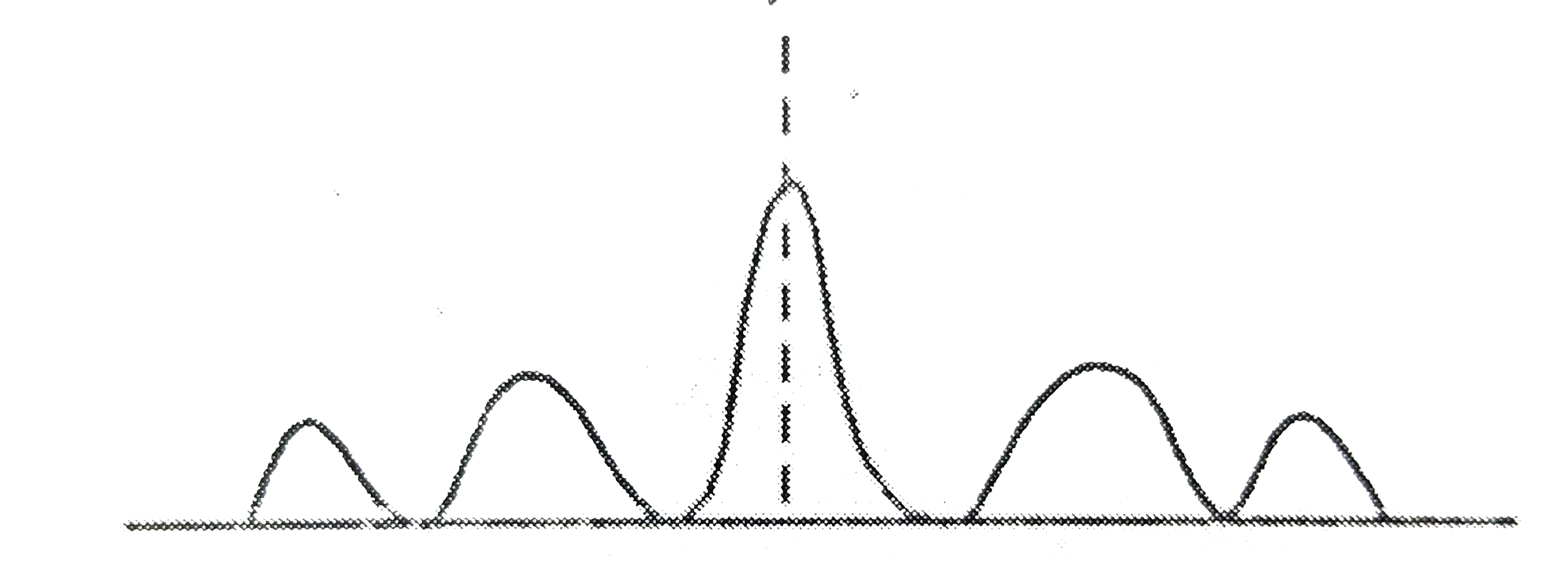
(a) Obtain the conditions for the formation of central maximum and secondary maxima and the minima.
(b) Why is there significant fall in intensity of the secondary maxima compared to the central maximum, whereas in double slit experiment all the bright fringes are of the same intensity ?
(c) When the width of the slit is made double the original width, how is the size of the central band affected ?
View Solution(i) In Young's double slit experiment the condition for (a) constructive and (b ) destructive interference at a point on the screen .
View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength λ. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as

View SolutionSuppose f(x) is differentiable at x=a. Then , necessary condition for f(x) to possess local maxima or local minima at x=a is
View Solution
