Na2[PtBrClI](CN)]
No of geometrical isomers =x
No of optical isomers =y
No of ions produced in
aqueous solution =z
Fine the value of x+y+z
Na2[PtBrClI(CN)]
The correct Answer is:6
To solve the problem, we will analyze the given complex compound Na2(PtBrClI(CN)) step by step to find the values of x, y, and z.
Step 1: Determine the Number of Geometrical Isomers (x)
1. Identify the central atom and ligands: The central atom is platinum (Pt), and it is coordinated by four different ligands: bromine (Br), chlorine (Cl), iodine (I), and cyanide (CN).
2. Check for geometrical isomerism: Since there are four different ligands attached to the platinum, we can have geometrical isomers. The possible arrangements can be determined by fixing one ligand and rotating the others.
3. Count the geometrical isomers:
- Fix one ligand (e.g., Br) and consider the arrangements of the other three (Cl, I, CN).
- The possible arrangements yield three distinct geometrical isomers:
1. Br, Cl, I, CN
2. Br, I, Cl, CN
3. Br, CN, Cl, I
Thus, the total number of geometrical isomers x=3.
Step 2: Determine the Number of Optical Isomers (y)
1. Check for optical activity: A compound exhibits optical isomerism if it lacks a plane of symmetry.
2. Analyze the structure: Since the compound is planar and has a plane of symmetry (due to the arrangement of the four different ligands around Pt), it does not exhibit optical isomerism.
Thus, the number of optical isomers y=0.
Step 3: Determine the Number of Ions Produced in Aqueous Solution (z)
1. Dissociation in water: When Na2(PtBrClI(CN)) is dissolved in water, it dissociates into its constituent ions.
2. Write the dissociation equation:
Na2(PtBrClI(CN))→2Na++(PtBrClI(CN))2−
3. Count the ions:
- From the dissociation, we have 2 sodium ions (Na+).
- The complex ion (PtBrClI(CN))2− counts as one additional ion.
Thus, the total number of ions produced z=2+1=3.
Final Calculation
Now, we can calculate x+y+z:
x+y+z=3+0+3=6
Conclusion
The final answer is:
6
2. Check for geometrical isomerism: Since there are four different ligands attached to the platinum, we can have geometrical isomers. The possible arrangements can be determined by fixing one ligand and rotating the others.
- Fix one ligand (e.g., Br) and consider the arrangements of the other three (Cl, I, CN).
- The possible arrangements yield three distinct geometrical isomers:
1. Br, Cl, I, CN
2. Br, I, Cl, CN
3. Br, CN, Cl, I
Na2(PtBrClI(CN))→2Na++(PtBrClI(CN))2−
- From the dissociation, we have 2 sodium ions (Na+).
- The complex ion (PtBrClI(CN))2− counts as one additional ion.
x+y+z=3+0+3=6
6
Similar Questions
in (M)=x
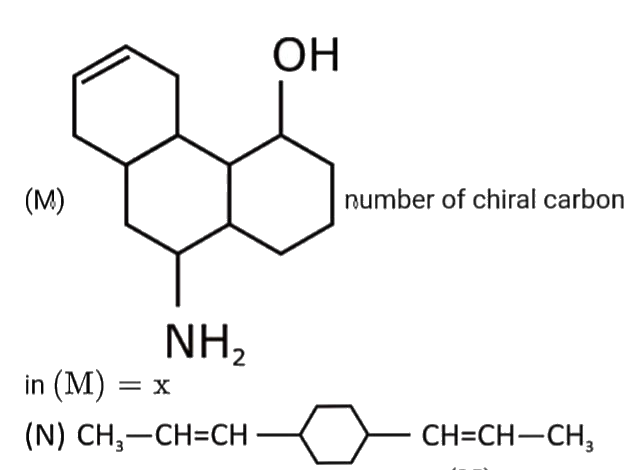
(Number of Geometrial isomers in (N)=y). The value of yx is
View SolutionCalculate the number of Na+ ion present in 142 amu of Na2SO4 in aqueous solution.
View SolutionIf 5, x, y, z, 405 are the first five terms of a geometric progression, find the values of x, y, and z.
View SolutionThe compounds whose stereochemical formula is written below exhibits x geometrical isomers and y optical isomers.
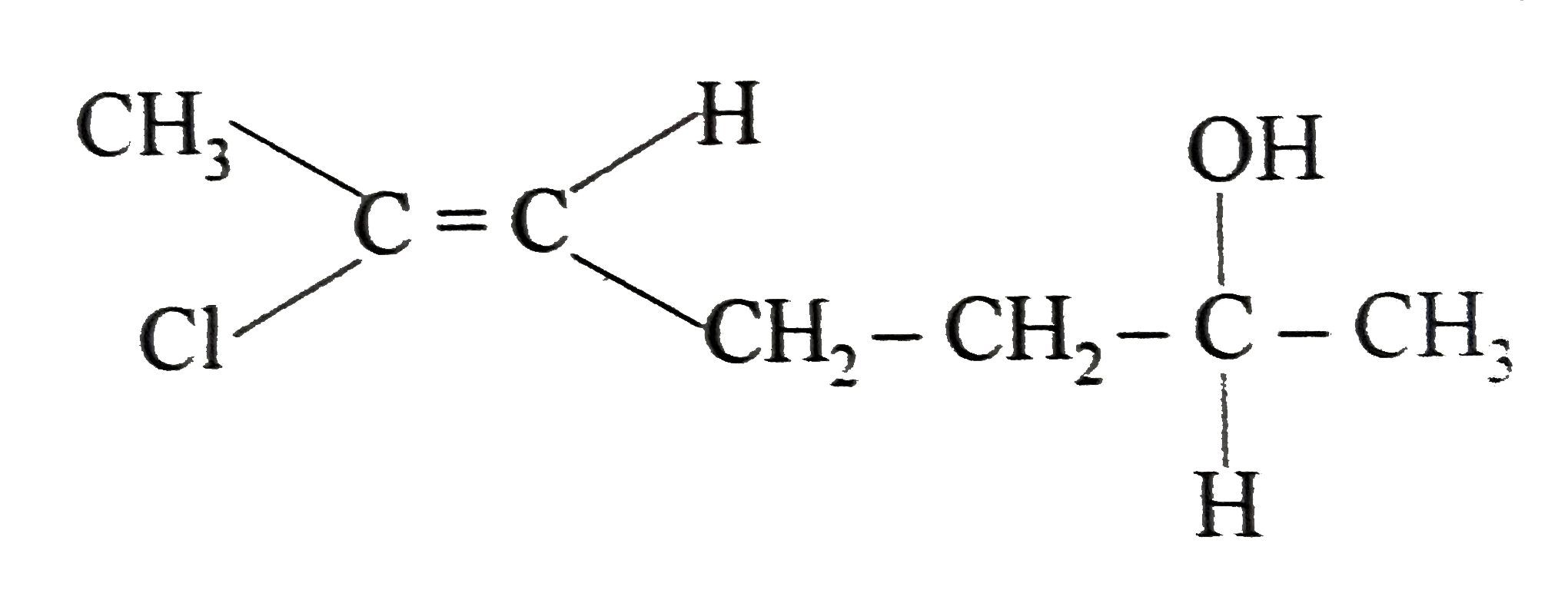
The values of x and y are
View SolutionObserve the compound 'M'

If in this compound
X=Total number of asymmetric C⋆ atoms
Y= Number of similar asymmetric C⋆ atoms
Z= Number of optically active stereoisomers
W= Number of optically inactive isomers
R= Number of geometrical orientations in space
Report your answer as : X +Y +Z+ W+ R
View SolutionDraw structures of geometrical isomers of [Fe(NH3)2(CN)4]−.
View Solution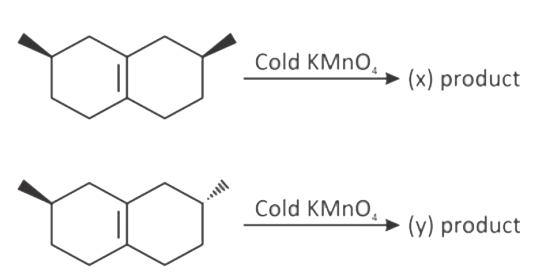
Find the value x+y2 (include sterio isomers)
View SolutionIf 2ax−2y+3z=0,x+ay+2z=0,and,2x+az=0 have a nontrivial solution, find the value of a.
View SolutionIf x−y+z=5andx2+y2+z2=49, find the value of :zx−xy−yz.
View SolutionIf x+y−z=4andx2+y2+z2=30, then find the value of xy−yz−zx
View Solution
