There are n identical red balls & m identical green balls. The number of different linear arrangements consisting of "n red balls but not necessarily all the green balls" is xCy then (A) x=m+n , y=m (B) x=m+n+1, y=m (C) x=m+n+1, y=m+1 (D) x=m+n, y=n
x=m+n
y=m
x=m+n+1
y=n
To solve the problem of finding the number of different linear arrangements consisting of "n red balls but not necessarily all the green balls," we can follow these steps:
Step 1: Understand the Problem
We have n identical red balls and m identical green balls. We want to arrange all n red balls and some (or none) of the m green balls in a linear fashion.
Step 2: Determine the Total Arrangements
When arranging n red balls and k green balls (where k can vary from 0 to m), the total number of balls in any arrangement will be n+k. The number of ways to choose k green balls from m is given by the binomial coefficient (mk).
Step 3: Use the Binomial Coefficient
The total number of arrangements for a fixed k is given by the formula for permutations of multiset:
Total arrangements=(n+k)!n!⋅k!
This can be rewritten using binomial coefficients:
Total arrangements=(n+kk)
Step 4: Sum Over All Possible k
Since k can take any value from 0 to m, we need to sum the arrangements for all possible k:
Total arrangements=m∑k=0(n+kk)
Step 5: Apply the Hockey Stick Identity
Using the hockey stick identity in combinatorics, we know:
m∑k=0(n+kk)=(n+m+1m)
This means the total number of arrangements can be expressed as:
Total arrangements=(n+m+1m)
Step 6: Identify x and y
From the expression (xy), we can identify:
- x=n+m+1
- y=m
Conclusion
Thus, the values of x and y are:
- x=m+n+1
- y=m
Final Answer
The correct option is (B) x=m+n+1,y=m.
We have n identical red balls and m identical green balls. We want to arrange all n red balls and some (or none) of the m green balls in a linear fashion.
When arranging n red balls and k green balls (where k can vary from 0 to m), the total number of balls in any arrangement will be n+k. The number of ways to choose k green balls from m is given by the binomial coefficient (mk).
The total number of arrangements for a fixed k is given by the formula for permutations of multiset:
Total arrangements=(n+k)!n!⋅k!
This can be rewritten using binomial coefficients:
Total arrangements=(n+kk)
Since k can take any value from 0 to m, we need to sum the arrangements for all possible k:
Total arrangements=m∑k=0(n+kk)
Using the hockey stick identity in combinatorics, we know:
m∑k=0(n+kk)=(n+m+1m)
This means the total number of arrangements can be expressed as:
Total arrangements=(n+m+1m)
From the expression (xy), we can identify:
- x=n+m+1
- y=m
Thus, the values of x and y are:
- x=m+n+1
- y=m
The correct option is (B) x=m+n+1,y=m.
Topper's Solved these Questions
Similar Questions
There are n−1 red balls, n green balls and n+1 blue balls in a bag. The number of ways of choosing two balls from the bag that have different colours is 299. What is the value of n?
View SolutionThe number of ways of arranging m positive and n(<m+1) negative signs in a row so that no two are together is a.= ^m+1pn b.=^n+1pm= c.=^m+1cn="" d.=^n+1cm
View SolutionMean of a certain number of observations is x . If each observation is divided by m(m≠0) and increased by n , then the mean of new observation is (a) xm+n (b) xn+m (c) x+nm (d) x+mn
View SolutionA bag contains 10 balls of which some are black and others are white. A person draws 6 balls & finds that 3 of them are white & 3 of them are black. Find probability that number of white balls in bag are same as black balls is mn , (where m and n are relatively prime) , then which of the following is/are True? m+n=43 (b) m−n=23 mn=330 (d) m+n=40
View SolutionIf xmyn=(x+y)m+n, prove that d2ydx2=0.
View SolutionGiven log x = m + n and log y = m - n, express the value of log10xy2 in terms of m and n.
View SolutionConsider a point A(m,n) , where m and n are positve intergers. B is the reflection of A in the line y=x, C is the reflaction of B in the y axis, D is the reflection of C in the x axis and E is the reflection of D is the y axis. The area of the pentagon ABCDE is a. 2m(m+n) b. m(m+3n) c. m(2m+3n) d. 2m(m+3n)
View Solutionin (M)=x
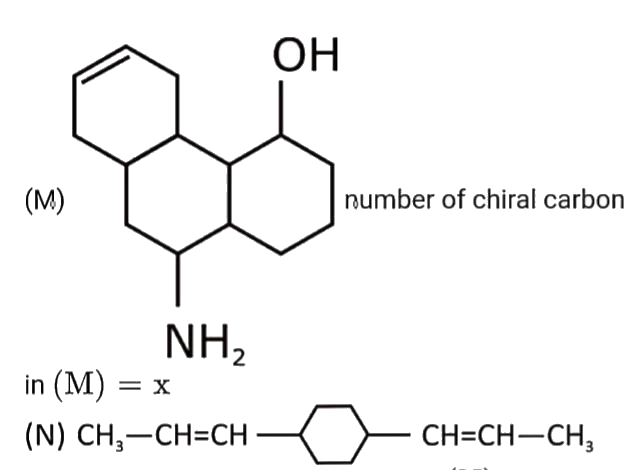
(Number of Geometrial isomers in (N)=y). The value of yx is
View SolutionIf a, m, n are positive integers, then {m√n√a}mn is equal to
(a) amn
(b) a
(c) amn
(d) 1
View SolutionIf a,x1,x2,…,xkandb,y1,y2,…,yk from two A. Ps with common differences mandn respectively, the the locus of point (x,y), wherex=∑ki=1xikand y=∑ki=1yik is: (A) (x−a)m=(y−b)n (B) (x−m)a=(y−n)b (C) (x−n)a=(y−m)b (D) (x−a)n=(y−b)m
View Solution
