A∘m value cannot be determined graphically , the plot between Am verses C1/2 for which of the following compound.
KCl
K2SO4
NH4OH
NaNO3
The correct Answer is:C
To solve the question regarding the molar conductivity at infinite dilution (A_m^(@)) and its graphical determination, we can follow these steps:
1. Understand the Concept of Molar Conductivity:
- Molar conductivity (A_m) is a measure of how well an electrolyte conducts electricity in solution. It is defined as the conductivity of the solution divided by the molar concentration of the electrolyte.
2. Identify Strong vs. Weak Electrolytes:
- Strong electrolytes completely dissociate into ions in solution, leading to a linear relationship between molar conductivity (A_m) and the square root of concentration (C^(1/2)).
- Weak electrolytes do not completely dissociate, resulting in a non-linear relationship between A_m and C^(1/2).
3. Graphical Determination:
- For strong electrolytes, the plot of A_m versus C^(1/2) will yield a straight line, allowing for the determination of A_m^(@) graphically.
- For weak electrolytes, the plot will not be linear, making it impossible to determine A_m^(@) graphically.
4. Analyze the Given Compounds:
- KCl: Strong electrolyte
- K2SO4: Strong electrolyte
- NaNO3: Strong electrolyte
- NH4OH: Weak electrolyte
5. Conclusion:
- Since NH4OH (ammonium hydroxide) is a weak electrolyte, the value of molar conductivity at infinite dilution (A_m^(@)) cannot be determined graphically.
Final Answer:
The compound for which the value of molar conductivity at infinite dilution cannot be determined graphically is NH4OH (option 3).
---
- Molar conductivity (A_m) is a measure of how well an electrolyte conducts electricity in solution. It is defined as the conductivity of the solution divided by the molar concentration of the electrolyte.
- Strong electrolytes completely dissociate into ions in solution, leading to a linear relationship between molar conductivity (A_m) and the square root of concentration (C^(1/2)).
- Weak electrolytes do not completely dissociate, resulting in a non-linear relationship between A_m and C^(1/2).
- For strong electrolytes, the plot of A_m versus C^(1/2) will yield a straight line, allowing for the determination of A_m^(@) graphically.
- For weak electrolytes, the plot will not be linear, making it impossible to determine A_m^(@) graphically.
- KCl: Strong electrolyte
- K2SO4: Strong electrolyte
- NaNO3: Strong electrolyte
- NH4OH: Weak electrolyte
- Since NH4OH (ammonium hydroxide) is a weak electrolyte, the value of molar conductivity at infinite dilution (A_m^(@)) cannot be determined graphically.
The compound for which the value of molar conductivity at infinite dilution cannot be determined graphically is NH4OH (option 3).
Similar Questions
Using constraint method find the relation between of a1 and a2.
 View Solution
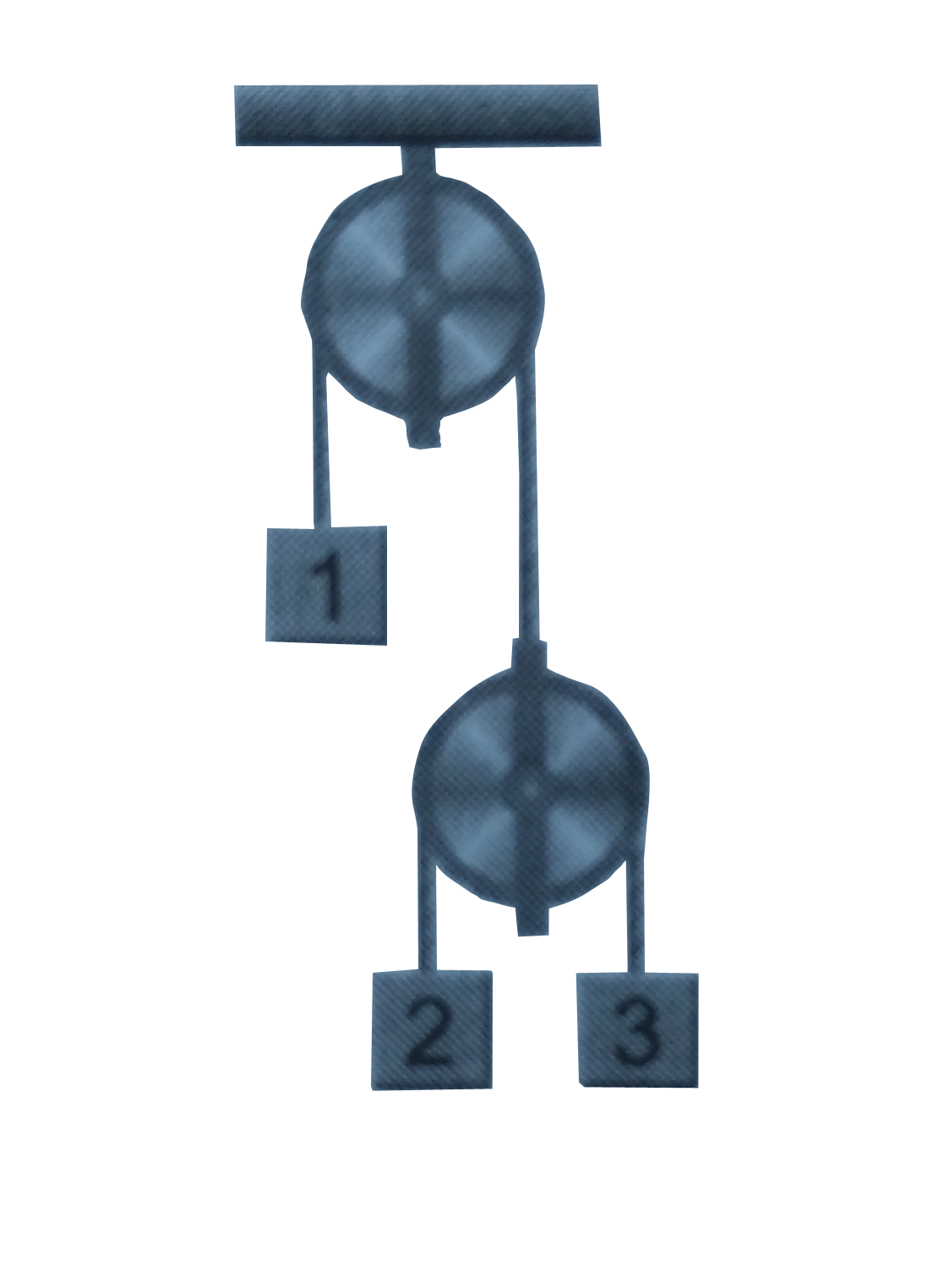
View SolutionA pulley-block arrangement is shown in the adjacent figure, if acceleration of m1,m2 and m3 are a1,a2 and a3 respectively, then relation between a1,a2 and a3 is ( All string and pulleys are ideal . )
 View Solution
View SolutionMake the constraint relation between a1,a2 and a3
 View Solution
View SolutionLet points A1,A2andA3 lie on the parabola y2=8x. If △A1A2A3 is an equilateral triangle and normals at points A1,A2andA3 on this parabola meet at the point (h, 0). Then the value of h I s
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratioView SolutionIn algebra, the determinant is useful value that can be computer from the elements of a square matrix. The determinant is represented as det 'A' or |A| and its value can be evaluated by the expansion of the determinant as given below
(A) Expansion of two order determinant :
(B) Expansion of 3rd order determinant
(i) With respect to first fow :
|A|=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=a1∣∣∣b2c2b3c3∣∣∣−b1∣∣∣a2c2a3c3∣∣∣+c1∣∣∣a2b2a3b3∣∣∣
=a1(b2c3−b3c2)−b1(a2c3−a3c2)+c1(a2b3−b2a3)
(ii) With respect to second column :
|A|=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=−b1∣∣∣a2c1a3c3∣∣∣+b2∣∣∣a1c1a3c3∣∣∣−b3∣∣∣a1c1a2c2∣∣∣
Similarly a determinant can be expanded with respect to any row or column
The value of k for which determinant ∣∣ ∣∣23−1−1−2k1−41∣∣ ∣∣ vanishes, is
(a) -3 (b) 7/11 (c) -2 (d) 2View SolutionIn algebra, the determinant is useful value that can be computer from the elements of a square matrix. The determinant is represented as det 'A' or |A| and its value can be evaluated by the expansion of the determinant as given below
(A) Expansion of two order determinant :
(B) Expansion of 3rd order determinant
(i) With respect to first fow :
|A|=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=a1∣∣∣b2c2b3c3∣∣∣−b1∣∣∣a2c2a3c3∣∣∣+c1∣∣∣a2b2a3b3∣∣∣
=a1(b2c3−b3c2)−b1(a2c3−a3c2)+c1(a2b3−b2a3)
(ii) With respect to second column :
|A|=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=−b1∣∣∣a2c1a3c3∣∣∣+b2∣∣∣a1c1a3c3∣∣∣−b3∣∣∣a1c1a2c2∣∣∣
Similarly a determinant can be expanded with respect to any row or column
The value of the determinant ∣∣ ∣∣2346571−32∣∣ ∣∣is: (a) 54 (b) 40 (c) -45 (d) -40View SolutionIn algebra, the determinant is useful value that can be computer from the elements of a square matrix. The determinant is represented as det 'A' or |A| and its value can be evaluated by the expansion of the determinant as given below
(A) Expansion of two order determinant :
(B) Expansion of 3rd order determinant
(i) With respect to first fow :
|A|=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=a1∣∣∣b2c2b3c3∣∣∣−b1∣∣∣a2c2a3c3∣∣∣+c1∣∣∣a2b2a3b3∣∣∣
=a1(b2c3−b3c2)−b1(a2c3−a3c2)+c1(a2b3−b2a3)
(ii) With respect to second column :
|A|=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=−b1∣∣∣a2c1a3c3∣∣∣+b2∣∣∣a1c1a3c3∣∣∣−b3∣∣∣a1c1a2c2∣∣∣
Similarly a determinant can be expanded with respect to any row or column.
The vaue of the determinant ∣∣∣5132∣∣∣is: (a) 4 (b) 5 (c) 6 (d) 7View SolutionA mass M, attached to a horizontal spring, excutes SHM with a amplitude A1. When the mass M passes through its mean position then a smaller mass m is placed over it and both of them move together with amplitude A2, the ratio of (A1A2) is :
View SolutionA squence of positive terms A1,A2,A3,....,An satisfirs the relation An+1=3(1+An)(3+An). Least integeral value of A1 for which the sequence is decreasing can be
View Solution

