A line $L$ is perpendicular to the line $3 x - 4 y - 7 = 0$ and touches the circle $x^{2} + y^{2} - 2 x - 4 y - 4 = 0$ , the $y$ -intercept of the line $L$ can be:

A

$\frac{25}{3}$

B

$\frac{20}{3}$

C

$\frac{17}{3}$

D

$\frac{4}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Line perpendicular to $3 x - 4 y - 7 = 0$ is $4 x + 3 y + λ = 0$ ………(1)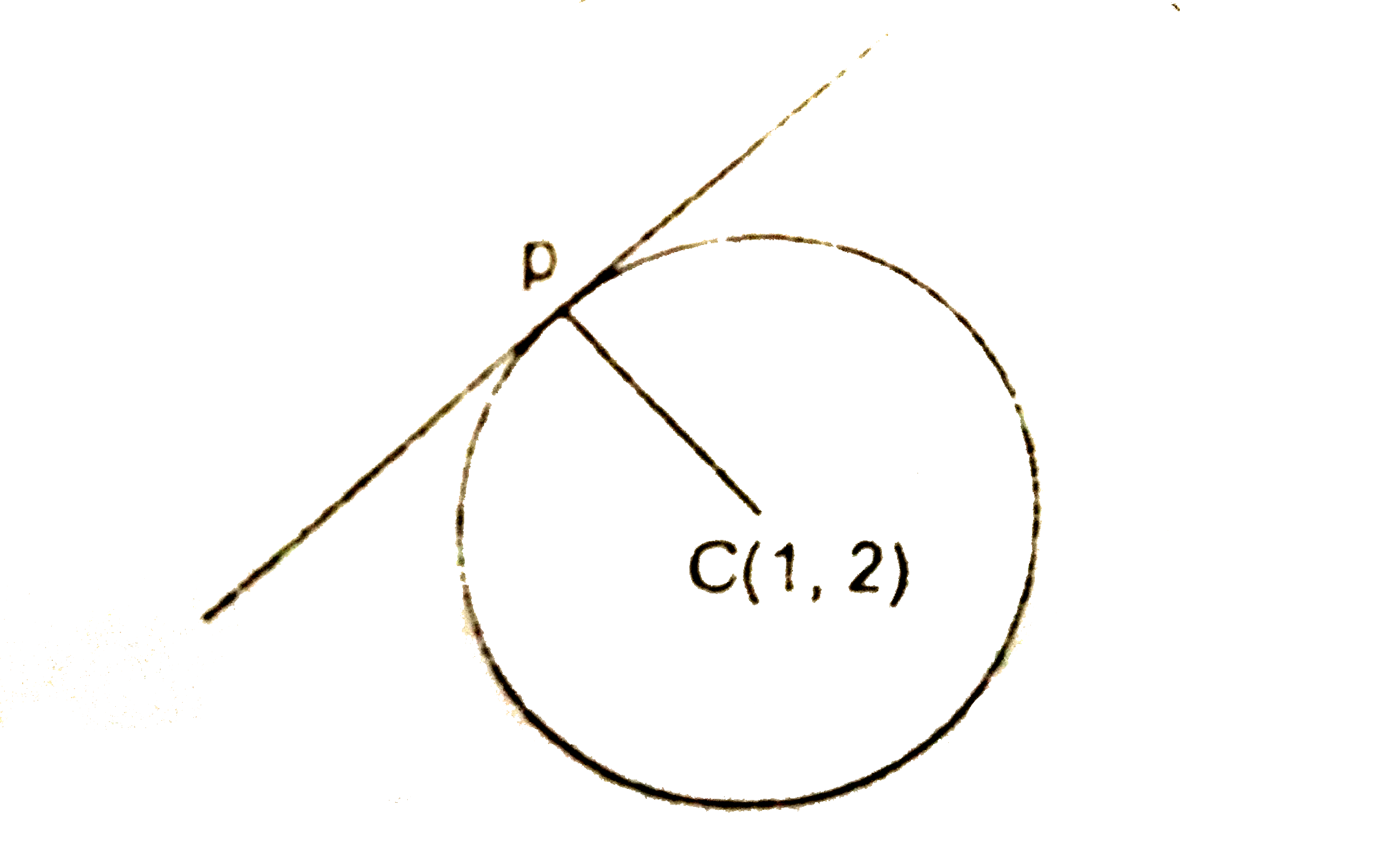
$C P = 3$
$\frac{| 4 + 6 + λ |}{\sqrt{25}} = 3 \Rightarrow | 10 + λ | = 15$
Line $L$ can be
$4 x + 3 y + 5 = 0$ or $4 x + 3 y - 25 = 0$
$y = - \frac{4}{3} x - \frac{5}{3}$ or $4 x + 3 y - 25 = 0$
$y = - \frac{4}{3} x - \frac{5}{3}$ or $y = - \frac{4}{3} x + \frac{25}{3}$
$∴$ possible intercept on $y$ -axis are $- \frac{5}{3} x + \frac{25}{3}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile