Consider equimolal aqueous solutions of NaHSO4 and NaCl with ΔTb and ΔT'b as their respective boiling point elevation . The value of limm→1ΔTbΔT'b will be :
1
1.5
3.5
23
The correct Answer is:B
To solve the problem, we need to find the ratio of the boiling point elevation (ΔTb) of an equimolal aqueous solution of NaHSO4 to that of NaCl as the molarity approaches 1.
1. Understanding Boiling Point Elevation:
The boiling point elevation is given by the formula:
ΔTb=i⋅m⋅Kb
where:
- ΔTb = boiling point elevation
- i = Van't Hoff factor (number of particles the solute dissociates into)
- m = molality of the solution
- Kb = ebullioscopic constant of the solvent (water in this case)
2. Identify the Van't Hoff Factor for Each Solute:
- For NaHSO4:
NaHSO4→Na++HSO−4
This dissociates into 3 ions: Na+, H+, and SO2−4. Therefore, i=3.
- For NaCl:
NaCl→Na++Cl−
This dissociates into 2 ions: Na+ and Cl−. Therefore, i=2.
3. Set Up the Ratios for Boiling Point Elevation:
Using the boiling point elevation formula for both solutions:
ΔTb=iNaHSO4⋅m⋅Kb=3⋅m⋅Kb
ΔT′b=iNaCl⋅m⋅Kb=2⋅m⋅Kb
4. Calculate the Ratio:
We want to find the limit of the ratio as m approaches 1:
ΔTbΔT′b=3⋅m⋅Kb2⋅m⋅Kb
The m and Kb cancel out:
ΔTbΔT′b=32
5. Final Answer:
Therefore, the value of limm→1ΔTbΔT′b is:
32=1.5
Conclusion:
The final answer is 1.5.
---
The boiling point elevation is given by the formula:
ΔTb=i⋅m⋅Kb
where:
- ΔTb = boiling point elevation
- i = Van't Hoff factor (number of particles the solute dissociates into)
- m = molality of the solution
- Kb = ebullioscopic constant of the solvent (water in this case)
- For NaHSO4:
NaHSO4→Na++HSO−4
This dissociates into 3 ions: Na+, H+, and SO2−4. Therefore, i=3.
- For NaCl:
NaCl→Na++Cl−
This dissociates into 2 ions: Na+ and Cl−. Therefore, i=2.
Using the boiling point elevation formula for both solutions:
ΔTb=iNaHSO4⋅m⋅Kb=3⋅m⋅Kb
ΔT′b=iNaCl⋅m⋅Kb=2⋅m⋅Kb
We want to find the limit of the ratio as m approaches 1:
ΔTbΔT′b=3⋅m⋅Kb2⋅m⋅Kb
The m and Kb cancel out:
ΔTbΔT′b=32
Therefore, the value of limm→1ΔTbΔT′b is:
32=1.5
The final answer is 1.5.
Topper's Solved these Questions
Similar Questions
How are ΔTb and ΔTf related to the molar mass of the solute?
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
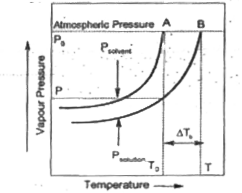
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality m then Ltm→0(ΔTbm) is equal to
View Solution
Knowledge Check
We have three aqueous solutions of NaCl labelled as A, B and C with concentration 0.1M,0.01and0.001 M , respectively . The value of van't Hoff factor for these solutions will be in the order :
AiA<iB<iCBiA>iB>iCCiA=iB=iCDiA>iB<iC
An aqueous solution freezes at
−0.186∘C(Kf=1.86∘ ,Kb=0.512∘. What is the elevation in boiling point?
View SolutionAn aqueous solution freezes on 0.36∘CKfandKb for water are 1.8 and 0.52 k kg mol−1 respectively then value of boiling point of solution as 1 atm pressure is
View Solution1.0 molal aqueous solution of an electrolyte X3Y2 is 25% ionized. The boiling point of the solution is (Kb for H2O=0.52Kkg/mol):
View Solution0.1 molal aqueous solution of an electrolyte AB3 is 90% ionised. The boiling point of the solution at 1 atm is (Kb(H2O)=0.52kg mol−1)
View SolutionWe have three aqueous solutions of NaCl labelled as A, B and C with concentration 0.1M,0.01and0.001 M , respectively . The value of van't Hoff factor for these solutions will be in the order :
View Solution1g of a non-volatile non-electrolyte solute is dissolved in 100g of two different solvents A and B whose ebullioscopic constants are in the ratio of 1 : 5. The ratio of the elevation in their boiling points, ΔTb(A)ΔTb(B) is
View SolutionGiven that ΔTf is the depression in freezing point of the solvent in a solution of a non-volatile solute of molarity m,the quantity Ltm→0(ΔTf/m) is equal to ……………. .
View Solution
