A steel wire of length 1 m, mass 0.1 kg and uniform cross-sectional area is rigidly fixed at both ends. The temperature of wire is lowered by 20°C. If transverse waves are set up by plucking the string in the middle, calculate the frequency (In S.I. units) of the fundamental mode of vibration. Young’s modulus of steel , coefficient of linear expansion of steel.
The correct Answer is:11
Step by step video & image solution for A steel wire of length 1 m, mass 0.1 kg and uniform cross-sectional area 10^(-6)m^(2) is rigidly fixed at both ends. The temperature of wire is lowered by 20°C. If transverse waves are set up by plucking the string in the middle, calculate the frequency (In S.I. units) of the fundamental mode of vibration. Young’s modulus of steel =2xx10^(11)N//m^(2), coefficient of linear expansion of steel=1.21xx10^(-6)(degC)^(-1). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART III
15 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART IV
9 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART I
21 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART I
19 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
The plane wave represented by an eqution of the form y = f(x-vt) implies the propagation along the positive x-axis without chang of shape with constant velocity v. Then
View SolutionA pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
the shape of the string is drawn at t=0 and lthe area of the pulse elclosed by the string and the x−string is measured. It will be equal to
View Solutionthe same progressive wave is reprsented by two group I and II. Graoup I shows how the displacement 'y' varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curvse m repersents.
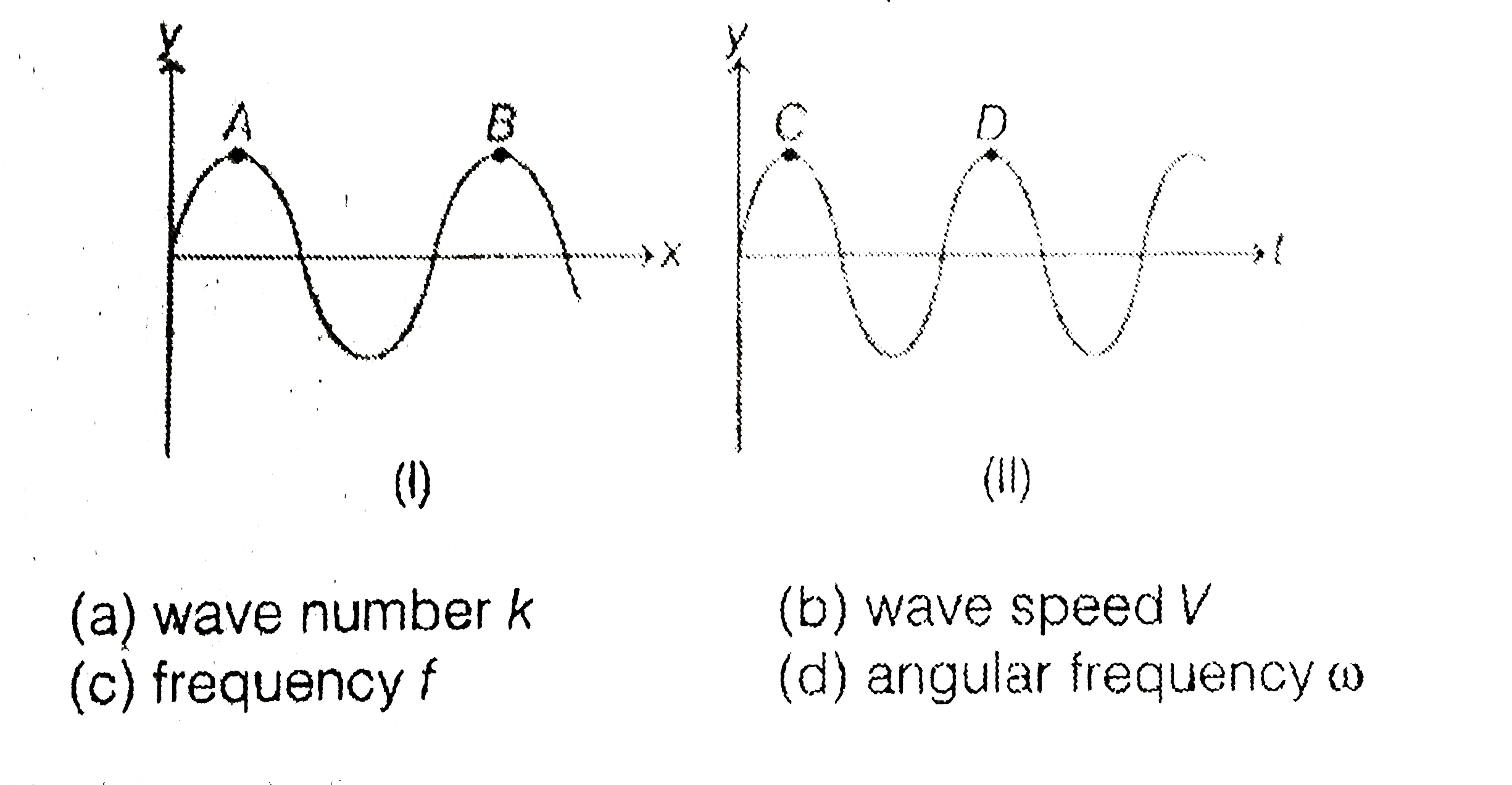
View SolutionA harmonically moving transverse wave on a string has a maximum particle velocity and acceleration of 3 m/s and 90m/s2 respectively. Velocity of the wave is 20m/s. Find the waveform.
View SolutionTwo parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I and I, respectively, find the resultant intensity at the focus.
View SolutionA steel wire of length 1m , mass 0.1kg and uniform cross-sectional area 10^(-6)m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If transverse calculate the frequency of the fundamental mode of vibration. Given for steel Y = 2 xx 10^(11)N//m^(2) alpha = 1.21 xx 10^(-5) per ^(@)C
View SolutionA steel wire is rigidly fixed at both ends its length mass and cross sectional area are 1m, 0.1 kg and 106m2 respectively then the temperature of the wire is lowered by 20∘C if the transverse waves are setup by plucking the wire at 0.25m from one end and assuming that wire vibrates with minimum number of loops possible for such a case. Find the frequency of vibration (in Hz). [coefficient of linear expansion of steel =1.21×10−6/.∘C and young's modulus =2×1011/N/m2]
View SolutionA steel wire of length 20 cm and uniform cross-section 1mm^(2) is tied rigidly at both the ends. If the temperature of the wire is altered from 40^(@)C to 20^(@)C , the change in tension. [Given coefficient of linear expansion of steel is 1.1xx10^(5) .^(@)C^(-1) and Young's modulus for steel is 2.0xx10^(11) Nm^(-2) ]
View SolutionA steel wire of length 1 m and mass 0.1 kg and having a uniform cross-sectional area of 10^(-6) m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If the wire is vibrating in fundamental mode, find the frequency (in Hz). (Y_(steel)=2xx 10^(11) N//m^(2),alpha_(steel)=1.21 xx 10^(-5)//.^(@)C) .
View SolutionA steel wire is rigidly fixed at both ends. Its length mass and cross-sectionl area are 1m, 0.1kg and 10−8m2 respectively. Tension in the wire is produced by lowering the temperature by 20∘C. If the transerverse waves are some up by plucking the wire at 0.25m from one end and assuming that the wire viberates with minimum number of loops possble for such a case. The frequency of viberation (in Hz) is found to be. 1.11. Find the value of K. Given α=1.21×10−5.∘C−1.Y−2×1011N/m2

View Solutionस्टील का एक तार जिसकी लम्बाई 1 मीटर, द्रव्यमान 0.1 किग्रा तथा एकसमान परिच्छेद-क्षेत्रफल 10−6 मीटर2 है, दोनों सिरों पर दृढ़तापूर्वक बँधा है। तार का ताप 20∘C कम कर दिया जाता है। यदि तार को मध्य में कर्षित करके (by plucking) अनुप्रस्थ तरंगें उत्पन्न की जायें, तो कम्पन की मूल विधा की आवृत्ति की गणना कीजिए। स्टील का यंग-प्रत्यास्थता गुणांक =2×1011 न्यूटन/मीटर2, स्टील का रेखीय प्रसार गुणांक =1.21×10−5 प्रति∘C.
View SolutionA steel wire of length 5 m and area of cross-section 4mm2 is stretched by 2 mm by the application of a force. If young's modulus of steel is 2×1011N/m2, then the energy stored in the wire is
View SolutionA steel wire of length 0.20m and uniform cross section 10^(-6)m^(2) is tied rigidly at both ends. The temperature of the wire is changed from 40^(@) C to 20^(@)C . Calculate the thermal tension in the wire given alpha =1.1. xx 10^(-5)//.^(@)C and Y=2xx10^(11)Nm^(-2)
View SolutionCalculate the force required to increase the length of a steel wire of cross- sectional area 10^(-6)m^(2) by 0.5% given: Y_(("for steel"))=2xx10^(11)N-m^(2)
View SolutionA steel wire of length 1 m, mass 0.1 kg and uniform cross sectional area 10^(-6)m^(2) is rigidly fixed at two ends. The temperature of the wire is lowered by 20^(@) C . If transverse waves are now set up by lucking the string at the middle, calculate the frequency of the fundamental tone. Givne, for steel, co-efficient of linear expansion = 1.21 xx 10^(-5_(@))C^(1) and Young's modulus = 2 xx 10 ^(11) N* m^(-2) .
View SolutionA steel wire of length lm, mass 0.1 kg and uniform cross-sectional area 10−6m2 is rigidly fixed at both ends. The temperature of the wire is lowered by 200C. If the transverse waves are set up by plucking the string in the middle, calculate the frequency of the fundamental mode of vibration [Y=2×1011N/m2andα=1.21×10−5l0C]
View Solution
