Two mirros are inclinded by an angle 30∘. An object is placed 10∘ with the mirror M1. Find the positons of first two images formed by each mirror. Find the total number of images using (i) direct formula and (ii) counting the images.
To solve the problem of finding the positions of the first two images formed by two mirrors inclined at an angle of 30∘ and an object placed at 10∘ with respect to mirror M1, we can follow these steps:
Step 1: Understanding the Setup
We have two mirrors, M1 and M2, inclined at an angle of 30∘. The object O is placed at an angle of 10∘ with respect to mirror M1.
Step 2: Finding the First Image from Mirror M1
- The first image I1 formed by mirror M1 will be at the same angle as the object but on the opposite side of the mirror.
- Since the object is at 10∘ with respect to M1, the image I1 will also be at 10∘ below M1.
Step 3: Finding the First Image from Mirror M2
- Now, we consider the object O with respect to mirror M2.
- The angle of the object with respect to mirror M2 can be calculated as:
Angle with M2=180∘−(30∘+10∘)=140∘
- The image I′1 formed by mirror M2 will be at an angle of 20∘ above M2 (since it reflects at the same angle).
Step 4: Finding the Second Image from Mirror M1
- Now, we consider the image I′1 as an object for mirror M1.
- The angle of I′1 with respect to mirror M1 is 20∘.
- Therefore, the second image I2 formed by mirror M1 will be at 20∘ below M1.
Step 5: Finding the Second Image from Mirror M2
- Next, we consider the image I2 as an object for mirror M2.
- The angle of I2 with respect to mirror M2 is 30∘+20∘=50∘.
- The second image I′2 formed by mirror M2 will be at 50∘ above M2.
Step 6: Counting the Total Number of Images
To find the total number of images, we can use two methods: the direct formula and counting the images.
Method (i): Direct Formula
- The formula for the number of images formed by two mirrors inclined at an angle θ is given by:
n=360∘θ
- Here, θ=30∘:
n=360∘30∘=12
- Since n is even, the total number of images is:
Total Images=n−1=12−1=11
Method (ii): Counting the Images
- We can also count the images formed by observing the angles:
1. 10∘ (from M1)
2. 20∘ (from M2)
3. 40∘ (from M1)
4. 50∘ (from M2)
5. Continuing this process until we reach angles close to 180∘.
After counting, we find that the total number of images formed is also 11.
Summary of Results
- The positions of the first two images are:
- I1 at 10∘ below M1
- I2 at 20∘ below M1
- The total number of images formed is 11.
We have two mirrors, M1 and M2, inclined at an angle of 30∘. The object O is placed at an angle of 10∘ with respect to mirror M1.
- The first image I1 formed by mirror M1 will be at the same angle as the object but on the opposite side of the mirror.
- Since the object is at 10∘ with respect to M1, the image I1 will also be at 10∘ below M1.
- Now, we consider the object O with respect to mirror M2.
- The angle of the object with respect to mirror M2 can be calculated as:
Angle with M2=180∘−(30∘+10∘)=140∘
- The image I′1 formed by mirror M2 will be at an angle of 20∘ above M2 (since it reflects at the same angle).
- Now, we consider the image I′1 as an object for mirror M1.
- The angle of I′1 with respect to mirror M1 is 20∘.
- Therefore, the second image I2 formed by mirror M1 will be at 20∘ below M1.
- Next, we consider the image I2 as an object for mirror M2.
- The angle of I2 with respect to mirror M2 is 30∘+20∘=50∘.
- The second image I′2 formed by mirror M2 will be at 50∘ above M2.
To find the total number of images, we can use two methods: the direct formula and counting the images.
- The formula for the number of images formed by two mirrors inclined at an angle θ is given by:
n=360∘θ
- Here, θ=30∘:
n=360∘30∘=12
- Since n is even, the total number of images is:
Total Images=n−1=12−1=11
- We can also count the images formed by observing the angles:
1. 10∘ (from M1)
2. 20∘ (from M2)
3. 40∘ (from M1)
4. 50∘ (from M2)
5. Continuing this process until we reach angles close to 180∘.
- The positions of the first two images are:
- I1 at 10∘ below M1
- I2 at 20∘ below M1
- The total number of images formed is 11.
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1
141 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
If two mirrors are inclined at some angle and an object is placed between the mirrors and there are 7 images formed for an object, then the angle between the mirrors is
View SolutionIf two mirrors are inclined at some angle θ. An object is placed between the mirrors and there are 5 images formed for an object, then θ is may be
View SolutionThe mirror are inclined at angle of 50∘. The number of images formed for an object placed in between the mirrors is
View SolutionA point object is placed (0,0) and a plane mirror 'M' is placed, inclined 30∘ with the x axis.
Find the position of image.

View SolutionAn object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by a mirror is
View SolutionAn object is placed between two plane mirrors inclined at an angle to each other. If the number of images formed is 7 then the angle of inclination is -
View SolutionAn object P is kept in front of two plane mirrors as shown in the figure. The number of image formed is k. Find out the value of k.
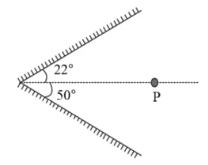
View SolutionWhen an object is placed between two parallel mirrors, then number of images formed are
View SolutionTwo plane mirrors are plaved parallel to each other and 40 cm apart. An a object is placed 10 cm from one mirror .What is the distance from the object to the image for each of the five images that are closest to the object?
View SolutionTwo plane mirror are inclined at an angle of 72∘. The number of images of a point object placed between them will be
View Solution
