A ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y)=[ky3/2+1]1/2 where k=1m−3/2 and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.
![A ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y) = [ky^(3//2) + 1 ]^(1//2) where k=1 m^(-3//2) and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_PHY_RK_JM_C18_E01_577_Q01.png)
60∘
53∘
sin−1(4/9)
no deviation at all
The correct Answer is:D
As n varies 'y' , parallel slabs can be taken , and we kown in parallel slabs nrsinir = constant . As n1sini1 =1×sin90∘=1 = constant
nfinal=nair=1
⇒1=1×sinrfinal⇒rfinal=90∘
:. Deviation is zero.
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
80 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
A ray of light travelling in air is inciden at angle of inciden 30∘ on one surface of slab in which refractive index varies with y. The light travels along the curve y=4x2 ( y and x are in meter) in the slab. Find out the refractive index of the slab at y=1/2m in the slab.

View SolutionA ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2 ,where k=1.0m−3/2.the refractive index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
View SolutionA light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
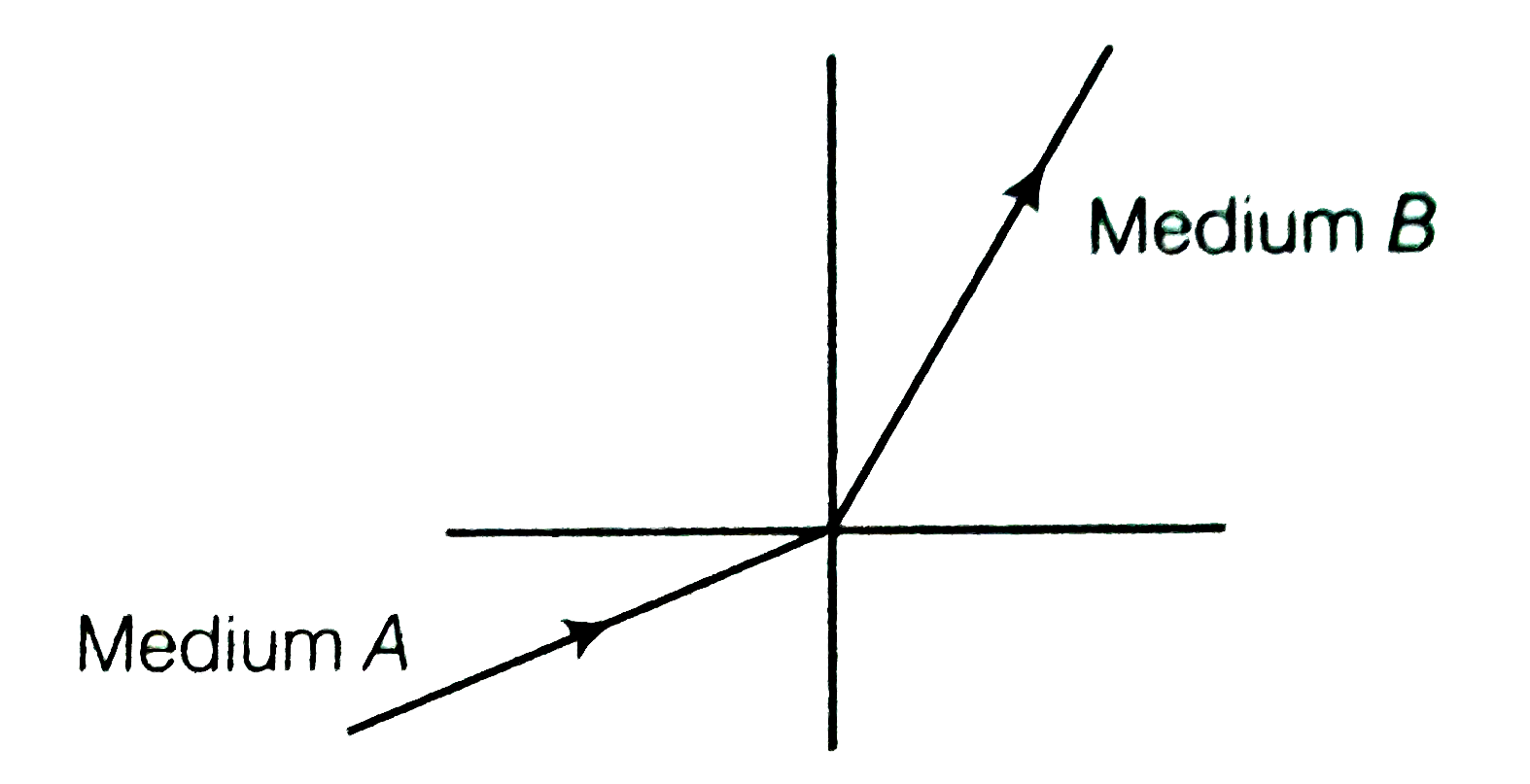
View SolutionA ray of light suffers a minimum deviation when incident on equilateral prism of refractive index √2 The angle of deviation is
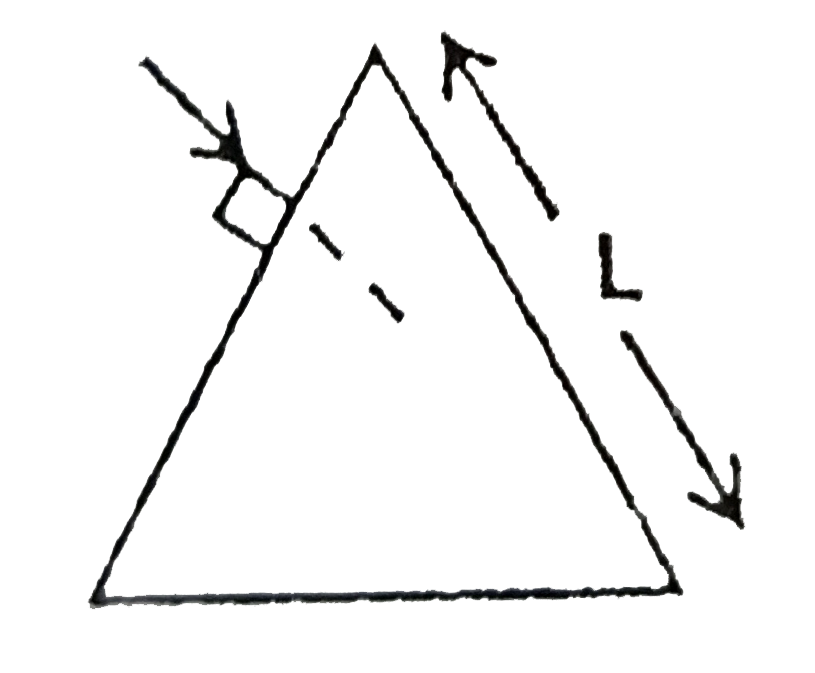
View SolutionThere is a equilateral prism of refractive index 3 on which a light ray is incident normally on one face as shown in the figure. Find the length of the path traveled by the light ray inside the prism.
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
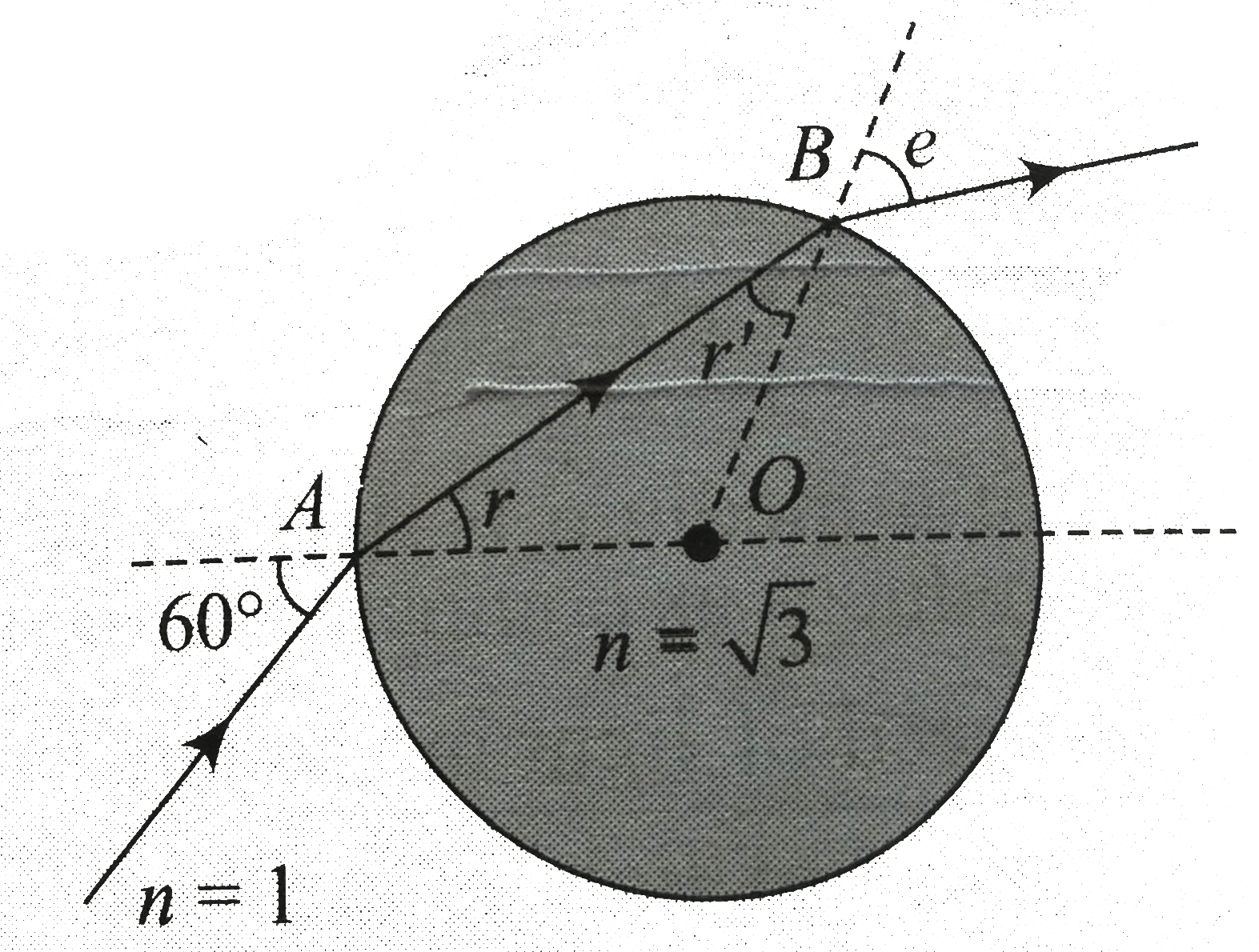
View SolutionTwo parts of long cylinder having refractive index √3 and 32 are arranged as shown in figure. When a light ray is incident an one plane surface as shown, total deviation produced in the path of light ray is π3xrad. Then calculate x.
 .
.
View SolutionA long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
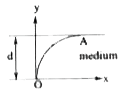
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
View SolutionA ray of light is incident on the surface of a sphere of refractive index √72 other half of sphere is silvered. After refraction it is reflected and then refracted out of sphere again such that the total deviation is minimum then total deviation of the ray will be (sin410−√37)

View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5)
View Solution
