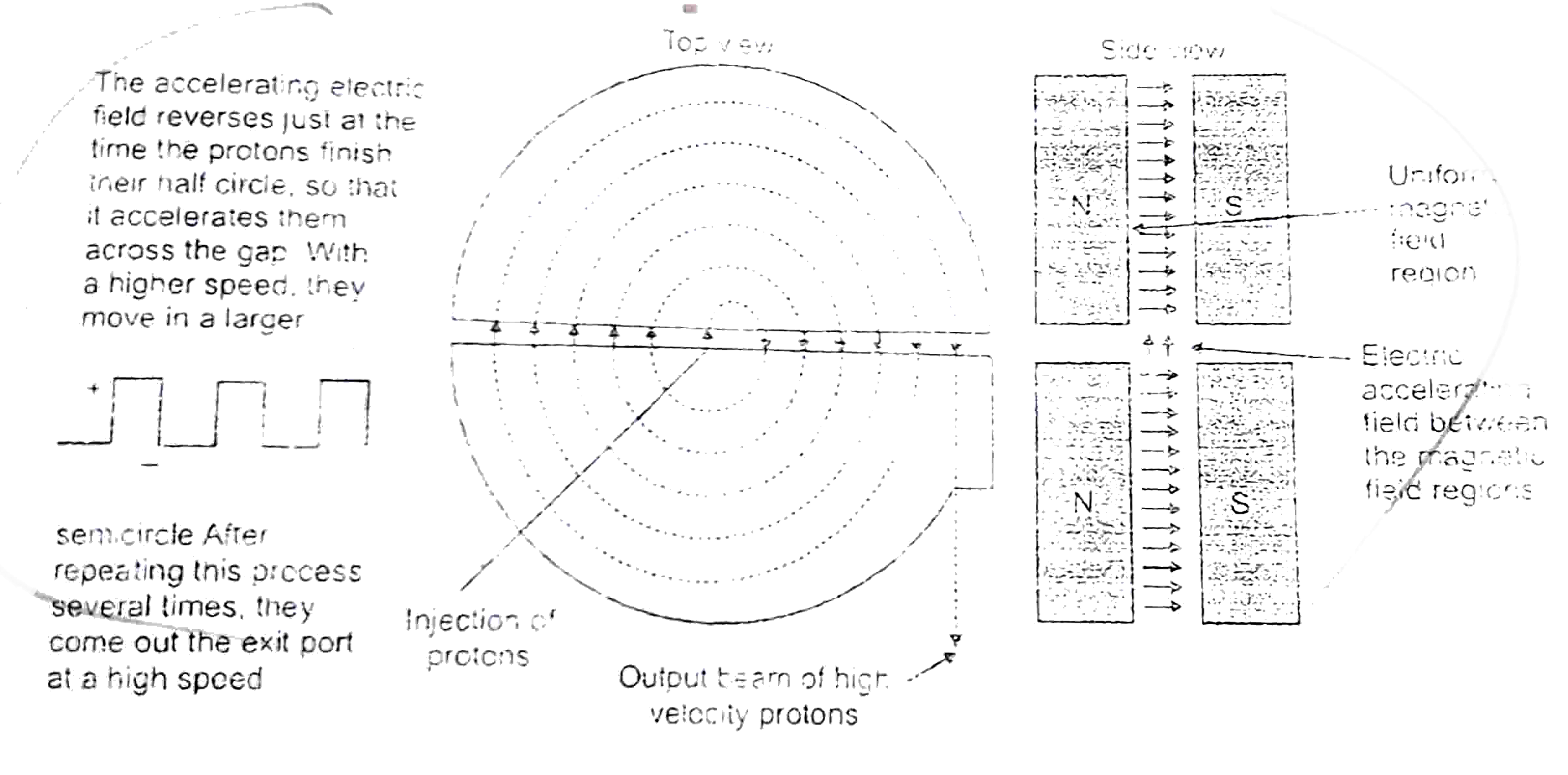
In the given figure of a cyclotron, showing the particle source and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by
...(1)
Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency of the electrical oscilliator, or ...(2)
This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency that is equal to the natural frequency at which the proton circulates in the magnetic field.
Combining equation and allows us to write the resonance condition as
..(3)
For the proton, and are fixed.The oscillator (we assume) is designed to work at a single fixed frequency We then "tune" the cyclotron by barying until eq. is satisfied and then many protons circulate through the magnetic field, to emerge as a beam.
If for a charge particle is ,frequency of applied is .Then applied magnetic field is
tesla
tesla
tesla
can not be defined
The correct Answer is:A
.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION-2
3 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION- 3
5 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3
18 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Curves in the graph shown in Fig. give, as function of radius distance r, the magnitude B of the magnetic field inside and outside four long wire a,b,c and d, carrying currents that are uniformly distributed across the cross sections of the wires. Overlapping portions of the plots are indicated by double labels.

Which wire has the greatest radius?
View SolutionTwo particles, each having a mass m are placed at a separation d in a uniform magnetic field B as shown in they have opposite charges of equal magnitude q. at time t =0, the particles are projectd towards each other,each with a speed v. suppose the coulomb force between the charges is switched off. (a) Find the maximum value vm of the projection speed so that the two particles do not collide. (b) What would be the minimum and maximum separation between the particles if v=vm2? (c) At what instant will a collision occur between the particles if v=2vm ? (d) Suppose v=2vm and the collision between the particles is completely inelastic. Describe the motion after the collision.

View SolutionA magnetic needls is kept in a non-unifrom magnetic field . It experinces
View SolutionAn electromagnetic wave of frequency υ=3 MHz passes from vacuum into a dielectric medium with permittivity ε=4. Then
View SolutionA long thin wire carrying a varying current I=i0sinωt lies at a distance y above one edge of a rectangular wire loop of length LandW lying in the x−z plane. What emf is induced in the loop?

View SolutionThe oscillating frequency of a cyclotron is 10 MHz . If the radius of its Dees is 0.5 m , the kinetic energy of a proton which is accelerated by the cyclotron is
View SolutionIn a cyclotron the radius of dees is R and the applied magnetic field has a magnitude of B. Particles having charge q and mass m are accelerated using this cyclotron and the maximum kinetic energy that can be imparted to a particle is k. (a) Find k in terms of R, B, q and m. (b) If protons and alpha particles are accelerated using this cyclotron which particle (proton or alpha) will gain more kinetic energy? (c) Can we use a cyclotron to impart very high kinetic energy to an electron?
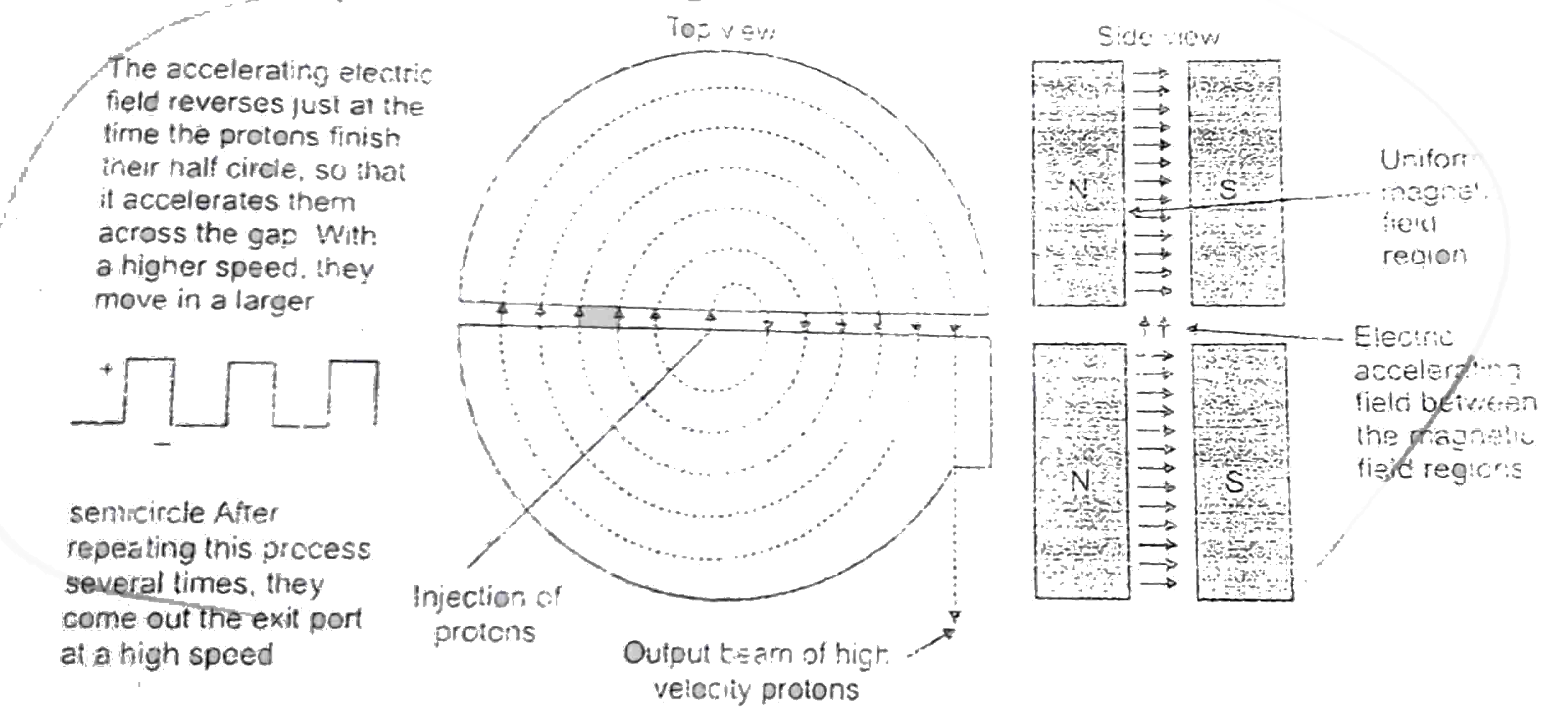
View SolutionIn the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by
r=mvqB...(1)
Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency fosc of the electrical oscilliator, or f=fosc(resonance condition)...(2)
This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency fosc that is equal to the natural frequency f at which the proton circulates in the magnetic field.
Combining equation 1 and 2 allows us to write the resonance condition as
qB=2πmfosc..(3)
For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency foscWe then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam.
Ratio of radius of successive semi circular path
View SolutionIn the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by r=(mv)/(qB) ...(1) Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency f_(osc) of the electrical oscilliator, or f=f_(osc)("resonance condition") ...(2) This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency f_(osc) that is equal to the natural frequency f at which the proton circulates in the magnetic field. Combining equation 1 and 2 allows us to write the resonance condition as qB=2pimf_(osc) ..(3) For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency f_(osc) We then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam. Change in kinetic energy of charge particle after every time period is:
View SolutionIn the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by r=(mv)/(qB) ...(1) Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency f_(osc) of the electrical oscilliator, or f=f_(osc)("resonance condition") ...(2) This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency f_(osc) that is equal to the natural frequency f at which the proton circulates in the magnetic field. Combining equation 1 and 2 allows us to write the resonance condition as qB=2pimf_(osc) ..(3) For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency f_(osc) We then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam. If q//m for a charge particle is 10^(6) ,frequency of applied AC is 10^(6)Hz .Then applied magnetic field is
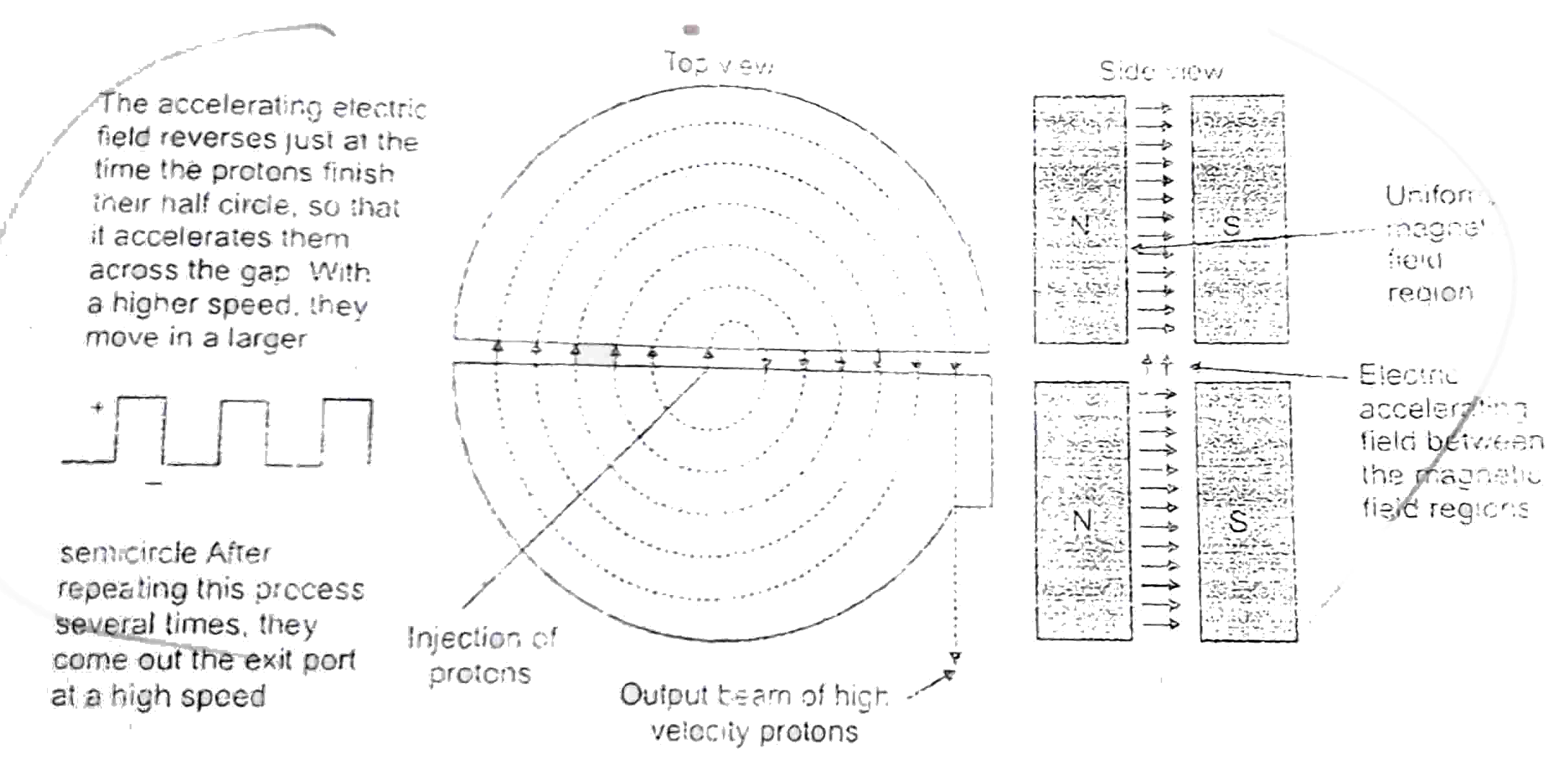
View SolutionIn the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by
r=mvqB...(1)
Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency fosc of the electrical oscilliator, or f=fosc(resonance condition)...(2)
This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency fosc that is equal to the natural frequency f at which the proton circulates in the magnetic field.
Combining equation 1 and 2 allows us to write the resonance condition as
qB=2πmfosc..(3)
For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency foscWe then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam.
Distance travelled in each time period are in the ratio of:
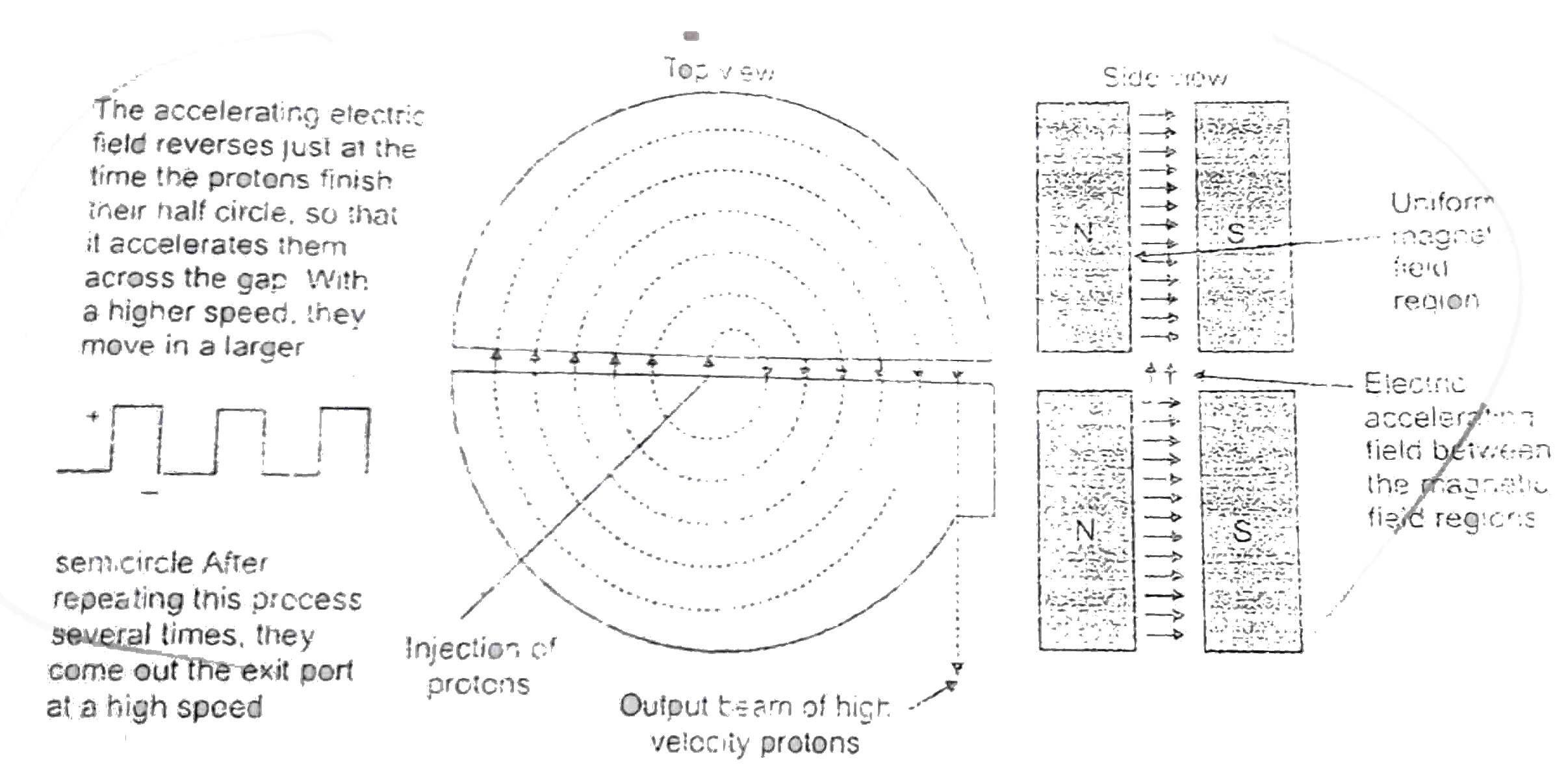
View SolutionIn the given figure of a cyclotron, showing the particle source S and the dees.A uniform magnetic field is directed up form the plane of the page.Circulating protons spiral outward within the hollow dees gaining energy every time they cross the gap between the dees.Suppose that a proton, injected by source S at the centre of the centre of the cyclotron in figure initially moves toward a negatively charged dee.It will accelerate toward this dee and enter it.Once inside, it is shielded from electric field by the copper walls of the dee,that is the electric field does not enter the dee.The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in circular path whose radius, which depends on its speed, is given by
r=mvqB...(1)
Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed.Thus, the proton again faces a negatively charged dee and is again accelerated.Thus,the proton again faces a negatively charged dee and is again accelerated.This process continues, the circulating proton always being in step.with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system.There a deflector plate sends it out through a portal.The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency fosc of the electrical oscilliator, or f=fosc(resonance condition)...(2)
This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency fosc that is equal to the natural frequency f at which the proton circulates in the magnetic field.
Combining equation 1 and 2 allows us to write the resonance condition as
qB=2πmfosc..(3)
For the proton, q and m are fixed.The oscillator (we assume) is designed to work at a single fixed frequency foscWe then "tune" the cyclotron by barying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam.
For a given charge particle a cyclotron can be "tune" by:
View SolutionA cyclotron is used to acclerate protons to a kinetic energy of 5 MeV. If the radius and the frequency field in the cyclotron is 2T. Find the radius and the frequency needed for the applied alternating voltage of the cyclotron. (Given : Velocity of proton =3×107m/s)
View SolutionIn a cyclotron a deutron gains maximum energy of 30 Mev. What is the maximum energy gained by a proton for the same cyclotron setting?
View SolutionA cyclotron is used to accelerate charged particles. Then the time period under the influence of 1T magnetic field of a proton :-
View SolutionA proton of charge e and mass "m" is accelerated in a cyclotron having an oscillator frequency f.The magnetic induction of the field in the cyclotron is B.If the radius of the D's is r ,the kinetic energy of the protons that come out of the cyclotron is
View Solution
