A 0.1M weak acid HA after teratment with 12 mL of strong base BOH has a pH of 5. At the end point, the volume of same base required is of acid is:
To solve the problem, we need to find the Ka of the weak acid HA after it has reacted with a strong base BOH. Here’s a step-by-step breakdown of how to approach this:
Step 1: Calculate the moles of the strong base BOH
Given:
- Concentration of BOH=0.1M
- Volume of BOH=12mL=0.012L
Using the formula:
Moles of BOH=Concentration×Volume=0.1M×0.012L=0.0012moles=1.2mmol
Step 2: Calculate the moles of the weak acid HA
Given:
- Concentration of HA=0.1M
- Volume of HA=27mL=0.027L
Using the formula:
Moles of HA=Concentration×Volume=0.1M×0.027L=0.0027moles=2.7mmol
Step 3: Determine the limiting reagent and remaining moles after reaction
- Moles of HA initially = 2.7 mmol
- Moles of BOH initially = 1.2 mmol
Since BOH is the limiting reagent, it will react completely:
- Moles of HA remaining = Initial moles of HA - Moles of BOH
Remaining moles of HA=2.7mmol−1.2mmol=1.5mmol
Step 4: Calculate the moles of salt formed
The salt formed from the reaction of HA and BOH is A−:
- Moles of salt A− formed = Moles of BOH reacted = 1.2 mmol
Step 5: Set up the pH equation using the Henderson-Hasselbalch equation
Given:
- pH = 5
- The Henderson-Hasselbalch equation is:
pH=pKa+log((Salt)(Acid))
Substituting the known values:
5=pKa+log(1.2mmol1.5mmol)
Step 6: Calculate the ratio of salt to acid
1.21.5=45
Thus, we can rewrite the equation:
5=pKa+log(45)
Step 7: Calculate log(45)
Using logarithmic properties:
log(45)=log(4)−log(5)≈0.602−0.699=−0.097
Step 8: Solve for pKa
Substituting back:
5=pKa−0.097
pKa=5+0.097=5.097
Step 9: Calculate Ka
Using the relationship between Ka and pKa:
Ka=10−pKa=10−5.097
Calculating this gives:
Ka≈8×10−6
Final Answer
The Ka of the weak acid HA is approximately 8×10−6.
---
Given:
- Concentration of BOH=0.1M
- Volume of BOH=12mL=0.012L
Moles of BOH=Concentration×Volume=0.1M×0.012L=0.0012moles=1.2mmol
Given:
- Concentration of HA=0.1M
- Volume of HA=27mL=0.027L
Moles of HA=Concentration×Volume=0.1M×0.027L=0.0027moles=2.7mmol
- Moles of HA initially = 2.7 mmol
- Moles of BOH initially = 1.2 mmol
- Moles of HA remaining = Initial moles of HA - Moles of BOH
Remaining moles of HA=2.7mmol−1.2mmol=1.5mmol
The salt formed from the reaction of HA and BOH is A−:
- Moles of salt A− formed = Moles of BOH reacted = 1.2 mmol
Given:
- pH = 5
- The Henderson-Hasselbalch equation is:
pH=pKa+log((Salt)(Acid))
5=pKa+log(1.2mmol1.5mmol)
1.21.5=45
Thus, we can rewrite the equation:
5=pKa+log(45)
Using logarithmic properties:
log(45)=log(4)−log(5)≈0.602−0.699=−0.097
Substituting back:
5=pKa−0.097
pKa=5+0.097=5.097
Using the relationship between Ka and pKa:
Ka=10−pKa=10−5.097
Calculating this gives:
Ka≈8×10−6
The Ka of the weak acid HA is approximately 8×10−6.
Topper's Solved these Questions
- IONIC EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - PART-2 Single and double value integer type
9 Videos
- IONIC EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - partIII one or more than one options correct type
10 Videos
- IONIC EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Exercise 1 part 2 only one option correct type
25 Videos
- HYDROCARBONBOOK - RESONANCE ENGLISHCHAPTER - HYDROCARBONEXERCISE - ORGANIC CHEMISTRY(Hydrocarbon)
50 Videos
- IUPAC NOMENCLATURE & STRUCTURAL ISOMERISM BOOK - RESONANCE ENGLISHCHAPTER - IUPAC NOMENCLATURE & STRUCTURAL ISOMERISM EXERCISE - Advanced Level Problems Part-5
2 Videos
Similar Questions
A weak base BOH is titrated with strong acid HA. When 10mL of HA is added, the pH is 9.0 and when 25mL is added, pH is 8.0. The volume of acid required to reach the equivalence point is
View Solution40mL0.05M solution of sodium sesquicarbonate dehydrate (Na2CO3.NaHCO3.2H2O) is titrated against 0.05MHCl solution, xmL of acid is required to reach the phenolphthalein end point while mL of same acid were required when methyl organe indicator was used in a separate titration. Which of the following is (are) correct statements?
a.y−x=80mL
b. y+x=160mL
c. If the titration is started with phenolphthalein indicator and methyl orange is added at the end point, 2xmL of HCl would be required further to reach the end point
d. If the same volume of same solution is titrated against 0.10MNaOH,x/2mL of base would be required
View SolutionA weak base (BOH) with Kb=10−5 is titrated with a strong acid (HCl), At 3/4 th of the equivalence point, pH of the solution is:
View SolutionA strong acid is titrated with weak base. At equivalence point, pH will be :
View SolutionWhen 40mL of a 0.1M weak base, BOH is titrated with 0.01MHCl, the pH of the solution at the end point is 5.5. What will be the pH if 10mL of 0.10MNaOH is added to the resulting solution ?
View SolutionTo a 100 mL of 0.1 M weak acid HA solution 22.5 mL of 0.2 M solution of NaOH are added.Now, what volume of 0.1 M NaOH solution be added into above solution, so that pH of resulting solution be 4.7:
[Given :(Kb(A−)=5×10−10]
View SolutionA weak acid HA is found to be 3% dissociated in 0.1 M solution . Calculate the value of Ka
View SolutionWhen a 20 mL of 0.08 M weak base BOH is titrated with 0.08 M HCl, the pH of the solution at the end point is 5. What will be the pOH if 10 mL of 0.04 M NaOH is added to the resulting solution?
[Given:log2=0.30andlog3=0.48]
View SolutionThe best indicator for the detection of the end point in the titration of a weak acid and a strong base is
View Solution10 mL of H2A(weak diprotic acid) solution is titrated against 0.1M NaOH. pH of the solution is plotted against volume of strong base added and following observation is made. If pH of the solution at first equivalence point is pH1 and at second equivalence point is pH2. Calculate the value of (pH2−pH1) at 25∘C
Given for H2A,pKa1 =4.6 and pKa2 =8, log 25=1.4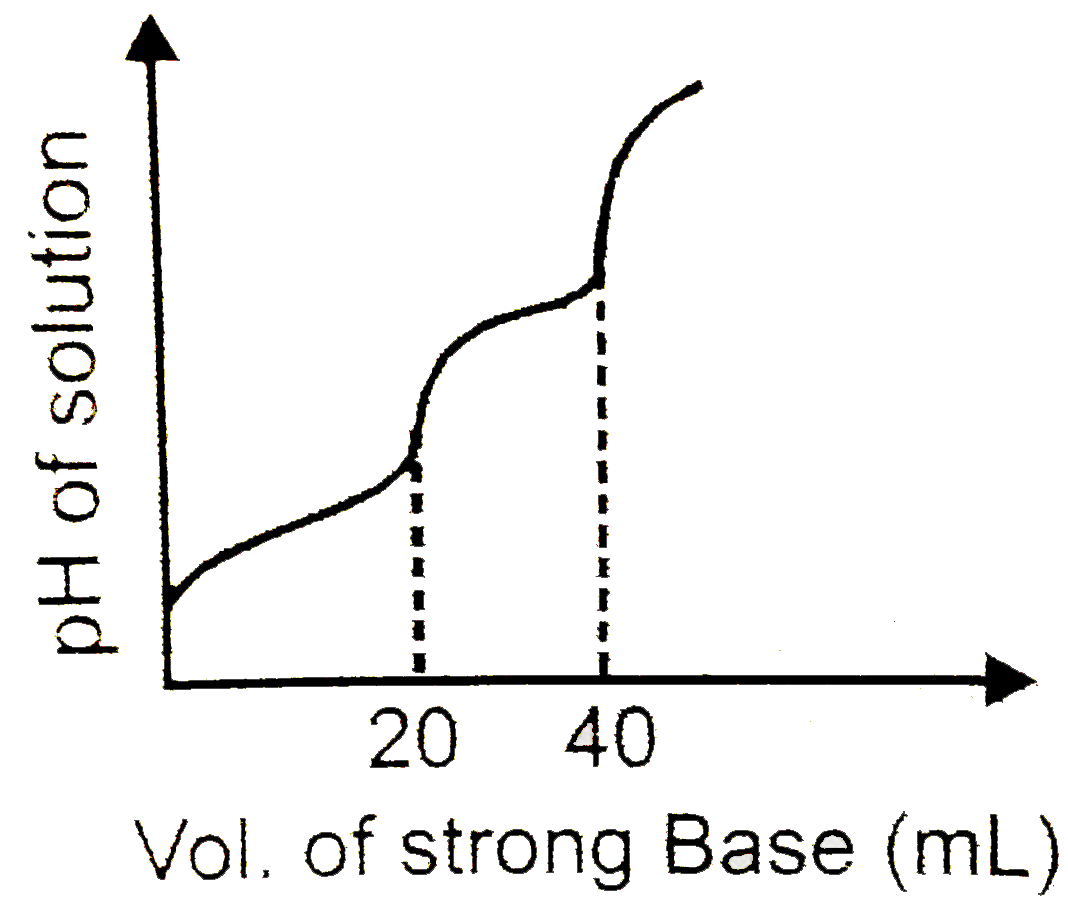
View Solution
