Question

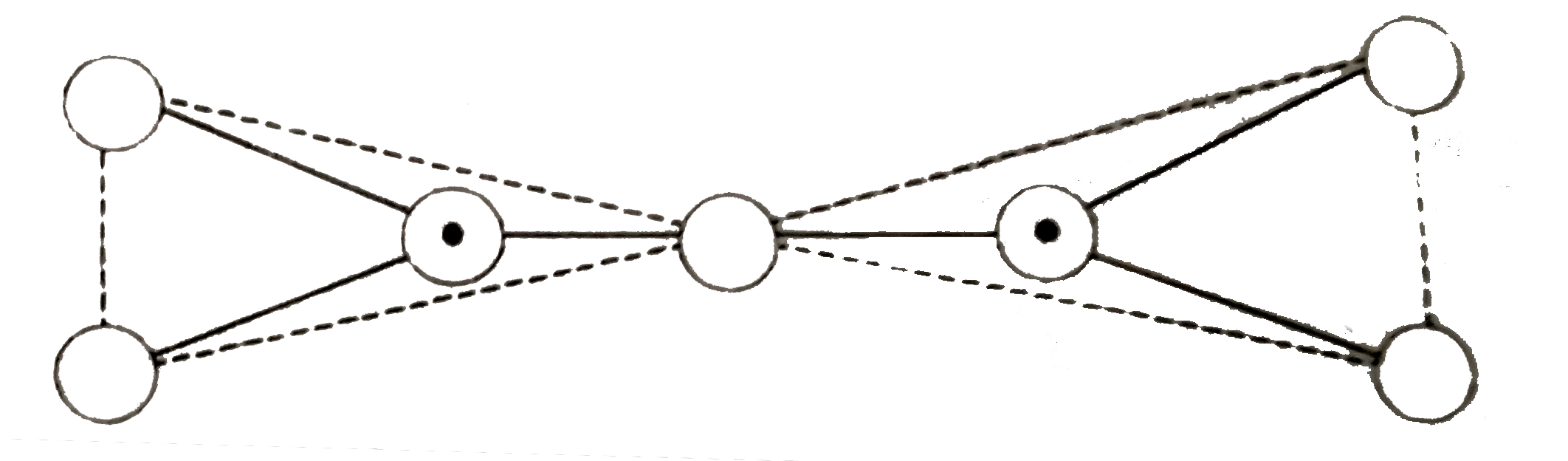
The silicate anion in the mineral kinoite is a chain of three $Si{O}_4$ tetrahedra, that share corners with adjacent tetrahedra. The charge of silicate anion is

Options

A. `-4`
B. `-8`
C. `-6`
D. `-2`

Answer

B

Explanation

To determine the charge of the silicate anion in the mineral kinoite, we will follow these steps:

Step 1: Identify the Structure of the Silicate Anion
The silicate anion in kinoite consists of three `SiO4` tetrahedra that share corners. This means we have three silicon atoms and a certain number of oxygen atoms.

Step 2: Count the Number of Silicon Atoms
Since there are three `SiO4` tetrahedra, we have:
- Number of silicon (Si) atoms = 3

Step 3: Count the Number of Oxygen Atoms
Each `SiO4` tetrahedron contains 4 oxygen atoms. However, because the tetrahedra share corners, we need to calculate the total number of unique oxygen atoms:
- In a chain of three `SiO4` tetrahedra, the number of oxygen atoms can be calculated as follows:
- The first tetrahedron contributes 4 oxygen atoms.
- The second tetrahedron shares one oxygen atom with the first, contributing 3 new oxygen atoms.
- The third tetrahedron shares one oxygen atom with the second, contributing 3 new oxygen atoms.

Thus, the total number of oxygen atoms is:
- Total oxygen = 4 (from the first tetrahedron) + 3 (from the second) + 3 (from the third) = 10

Step 4: Write the Formula for the Silicate Anion
From the above counts, we can write the formula for the silicate anion:
- The formula is `Si3O10`.

Step 5: Calculate the Charge of the Silicate Anion
Now, we need to calculate the overall charge of the silicate anion:
- The charge contributed by oxygen: Each oxygen atom has a charge of -2.
- Therefore, for 10 oxygen atoms:
\( \text{Charge from oxygen} = 10 \times (-2) = -20 \)

- The charge contributed by silicon: Each silicon atom has a charge of +4.
- Therefore, for 3 silicon atoms:
\( \text{Charge from silicon} = 3 \times (+4) = +12 \)

Step 6: Combine the Charges
Now, we combine the charges from silicon and oxygen to find the total charge of the silicate anion:
\( \text{Total charge} = \text{Charge from oxygen} + \text{Charge from silicon} = -20 + 12 = -8 \)

Conclusion
The charge of the silicate anion in the mineral kinoite is -8.

---