Calculate σ and π-bond in following compounds.
(a)HC≡CCH=CHCH3 ,(b)CH2=C=CHCH3
To calculate the sigma (σ) and pi (π) bonds in the given compounds, we will analyze each compound step by step.
Compound (a): HC≡C−CH=CH−CH₃
1. Draw the Structure:
- The compound can be represented as:
H−C≡C−CH=CH−CH₃
- Here, the first carbon (C) is bonded to one hydrogen (H) and has a triple bond with the second carbon (C).
- The second carbon (C) is bonded to the first carbon (C) and the third carbon (C) with a single bond.
- The third carbon (C) has a double bond with the fourth carbon (C) and is bonded to one hydrogen (H).
- The fourth carbon (C) is bonded to the third carbon (C) and the fifth carbon (C) with a single bond, and the fifth carbon (C) is bonded to three hydrogens (H).
2. Count the Sigma Bonds:
- Each single bond is a sigma bond.
- The triple bond consists of one sigma bond and two pi bonds.
- The double bond consists of one sigma bond and one pi bond.
- Counting the sigma bonds:
- C-H (1) + C≡C (1) + C-C (1) + C=CH (1) + C-H (1) + C-CH₃ (1) = 10 sigma bonds.
3. Count the Pi Bonds:
- The triple bond contributes 2 pi bonds.
- The double bond contributes 1 pi bond.
- Total pi bonds = 2 (from triple bond) + 1 (from double bond) = 3 pi bonds.
Summary for Compound (a):
- Sigma Bonds (σ): 10
- Pi Bonds (π): 3
---
Compound (b): CH₂=C=CH−CH₃
1. Draw the Structure:
- The compound can be represented as:
H₂C=C=CH−CH₃
- The first carbon (C) is bonded to two hydrogens (H) and has a double bond with the second carbon (C).
- The second carbon (C) has a double bond with the third carbon (C).
- The third carbon (C) is bonded to the fourth carbon (C) with a single bond, and the fourth carbon (C) is bonded to three hydrogens (H).
2. Count the Sigma Bonds:
- Counting the sigma bonds:
- C-H (2) + C=C (1) + C=C (1) + C-CH₃ (1) = 9 sigma bonds.
3. Count the Pi Bonds:
- The first double bond contributes 1 pi bond.
- The second double bond contributes 1 pi bond.
- Total pi bonds = 1 (from first double bond) + 1 (from second double bond) = 2 pi bonds.
Summary for Compound (b):
- Sigma Bonds (σ): 9
- Pi Bonds (π): 2
---
Final Results:
- For Compound (a):
- Sigma Bonds (σ): 10
- Pi Bonds (π): 3
- For Compound (b):
- Sigma Bonds (σ): 9
- Pi Bonds (π): 2
---
- The compound can be represented as:
H−C≡C−CH=CH−CH₃
- Here, the first carbon (C) is bonded to one hydrogen (H) and has a triple bond with the second carbon (C).
- The second carbon (C) is bonded to the first carbon (C) and the third carbon (C) with a single bond.
- The third carbon (C) has a double bond with the fourth carbon (C) and is bonded to one hydrogen (H).
- The fourth carbon (C) is bonded to the third carbon (C) and the fifth carbon (C) with a single bond, and the fifth carbon (C) is bonded to three hydrogens (H).
- Each single bond is a sigma bond.
- The triple bond consists of one sigma bond and two pi bonds.
- The double bond consists of one sigma bond and one pi bond.
- Counting the sigma bonds:
- C-H (1) + C≡C (1) + C-C (1) + C=CH (1) + C-H (1) + C-CH₃ (1) = 10 sigma bonds.
- The triple bond contributes 2 pi bonds.
- The double bond contributes 1 pi bond.
- Total pi bonds = 2 (from triple bond) + 1 (from double bond) = 3 pi bonds.
- Sigma Bonds (σ): 10
- Pi Bonds (π): 3
- The compound can be represented as:
H₂C=C=CH−CH₃
- The first carbon (C) is bonded to two hydrogens (H) and has a double bond with the second carbon (C).
- The second carbon (C) has a double bond with the third carbon (C).
- The third carbon (C) is bonded to the fourth carbon (C) with a single bond, and the fourth carbon (C) is bonded to three hydrogens (H).
- Counting the sigma bonds:
- C-H (2) + C=C (1) + C=C (1) + C-CH₃ (1) = 9 sigma bonds.
- The first double bond contributes 1 pi bond.
- The second double bond contributes 1 pi bond.
- Total pi bonds = 1 (from first double bond) + 1 (from second double bond) = 2 pi bonds.
- Sigma Bonds (σ): 9
- Pi Bonds (π): 2
- For Compound (a):
- Sigma Bonds (σ): 10
- Pi Bonds (π): 3
- Sigma Bonds (σ): 9
- Pi Bonds (π): 2
Topper's Solved these Questions
- IUPAC NOMENCLATURE & STRUCTURAL ISOMERISM BOOK - RESONANCE ENGLISHCHAPTER - IUPAC NOMENCLATURE & STRUCTURAL ISOMERISM EXERCISE - Bord Level Exercise
20 Videos
- IUPAC NOMENCLATURE & STRUCTURAL ISOMERISM BOOK - RESONANCE ENGLISHCHAPTER - IUPAC NOMENCLATURE & STRUCTURAL ISOMERISM EXERCISE - Exercise-1 Part-1 Section(A)
10 Videos
- IONIC EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - partIII one or more than one options correct type
10 Videos
- METALLURGYBOOK - RESONANCE ENGLISHCHAPTER - METALLURGYEXERCISE - ORGANIC CHEMISTRY(Alkyl Halide, Alcohol,Phenol,Ether)
17 Videos
Similar Questions
How many σ and π bonds are present in each of the following molecules?
(a) HC≡CCH=CHCH3 (b) CH2=C=CHCH3
View SolutionWrite IUPAC names of the following compounds : (a) CH3CH=C(CH3)2
(b) CH2=CH−C≡C−CH3
(c )
(d)
(e )
CH3(CH2)4CH(CH2)3CH3 ∣ CH2−CH(CH3)2
View SolutionFind out the number of sigma and pi bonds in the following molecules.
(a)C2H5Cl(b)CH2Cl2(c)CH3−CH=CH−C≡C−H
View SolutionIndicate the σ− and π− bonds in the following molecules:
I. C6H6 II. C6H12 III. CH2CI2
IV. CH2=C=CH2 V. CH3NO2
VI. HCONHCH3
View SolutionHow many π and σ bonds are in the given compound?
HC≡C−CH=CH2
View SolutionCalculate the number of σ,π and non-bonding (i.e lone pair) electrons in the following compounds
(a) H2C=CH−CH=CH2
(b) H3C−C≡C−CH=CH−CH3
(c) H3C−C∣CH3H−O∣∣C−C≡C−CH=CH−C≡N
View SolutionWrite the IUPAC name of the following compound :
CH2=CHCH2Br
View SolutionWrite the structures of geometrical isomers of the following compounds : (1) CHCOOH = CHCOOH (ii) C6H5−CH=CHCOOH (iii) CH2CH=CHCH3.
View SolutionThe decreasing order of bond dissociation energy of C-H bond in given compound is :-
(A) CH3−H (B) CH3−CH2−H
CH2=CH−CH2−H (D)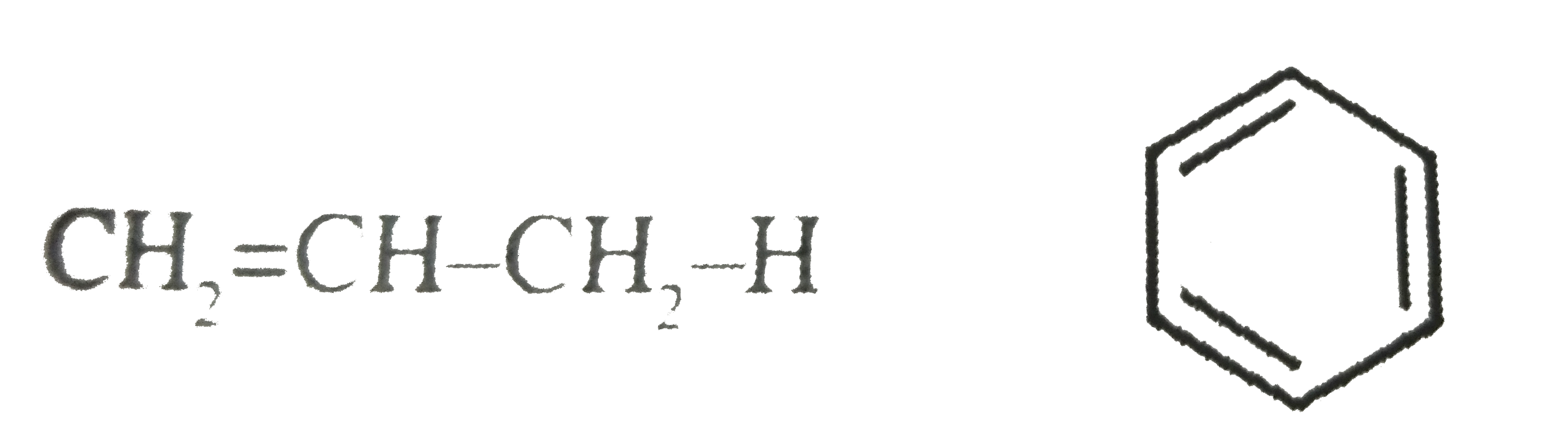
View SolutionIndicate the σ&π bonds in
(i) CH2Cl2
(ii) CH3−C≡C−CH3
View Solution
