In given figure, let ΔW and ΔW2 be the work done by the gas in process A and B respectively then (given change in volume is same in both process)
ΔW1>ΔW2
ΔW1=ΔW2
ΔW1<ΔW2
Nothing can be said about the relation between ΔW1 and ΔW2
The correct Answer is:C
To solve the problem regarding the work done by the gas in processes A and B, we will follow these steps:
Step 1: Understand the Work Done by a Gas
The work done by a gas during expansion or compression can be calculated using the formula:
ΔW=PΔV
where P is the pressure and ΔV is the change in volume.
Step 2: Identify the Processes
In the given question, we have two processes:
- Process A (at constant pressure PA)
- Process B (at constant pressure PB)
Step 3: Write the Expressions for Work Done
For process A, the work done ΔW1 can be expressed as:
ΔW1=PAΔV
For process B, the work done ΔW2 can be expressed as:
ΔW2=PBΔV
Step 4: Compare the Work Done
Since the change in volume ΔV is the same for both processes, we can compare the work done by taking the ratio:
ΔW1ΔW2=PAΔVPBΔV=PAPB
Step 5: Analyze the Pressure Values
From the problem statement, we know that the pressure PB is greater than PA (i.e., PB>PA). Therefore, the ratio PAPB will be less than 1:
PAPB<1
Step 6: Conclude the Comparison of Work Done
Since ΔW1ΔW2<1, we can conclude that:
ΔW1<ΔW2
Final Answer
Thus, the work done by the gas in process A is less than the work done in process B:
ΔW1<ΔW2
The work done by a gas during expansion or compression can be calculated using the formula:
ΔW=PΔV
where P is the pressure and ΔV is the change in volume.
In the given question, we have two processes:
- Process A (at constant pressure PA)
- Process B (at constant pressure PB)
For process A, the work done ΔW1 can be expressed as:
ΔW1=PAΔV
ΔW2=PBΔV
Since the change in volume ΔV is the same for both processes, we can compare the work done by taking the ratio:
ΔW1ΔW2=PAΔVPBΔV=PAPB
From the problem statement, we know that the pressure PB is greater than PA (i.e., PB>PA). Therefore, the ratio PAPB will be less than 1:
PAPB<1
Since ΔW1ΔW2<1, we can conclude that:
ΔW1<ΔW2
Thus, the work done by the gas in process A is less than the work done in process B:
ΔW1<ΔW2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise -2 Part-I: Only one option correct type23videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise-2 II: Single and double value integer type16videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - H-11videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY50videos
TEST SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
The work done in adiabatic process is given by
AnR(T1)−T2γBnR(T1)−T2γ−1C(nR(T1)−T2)RDγ(T1)−T2Rn
Find work done by the gas in the process shown in figure.
 View Solution
View SolutionIn given figure, let ΔU1 and ΔU2 be change in internal energy in process ABC and CDA respectively. ΔQ and W be the net heta given and net work done by the system in the process ABC+CDA, then
 View Solution
View SolutionThe work done by the gas in the process shown in given P-V diagram is
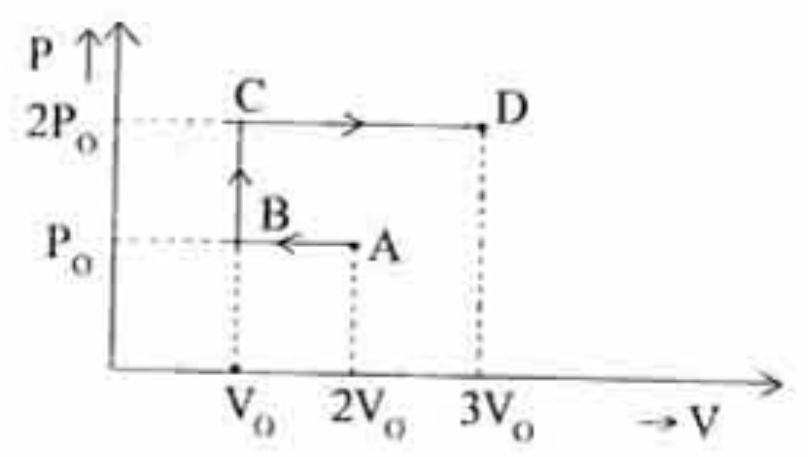 View Solution
View SolutionFind work done by the gas in the process AB shown in the following figures.
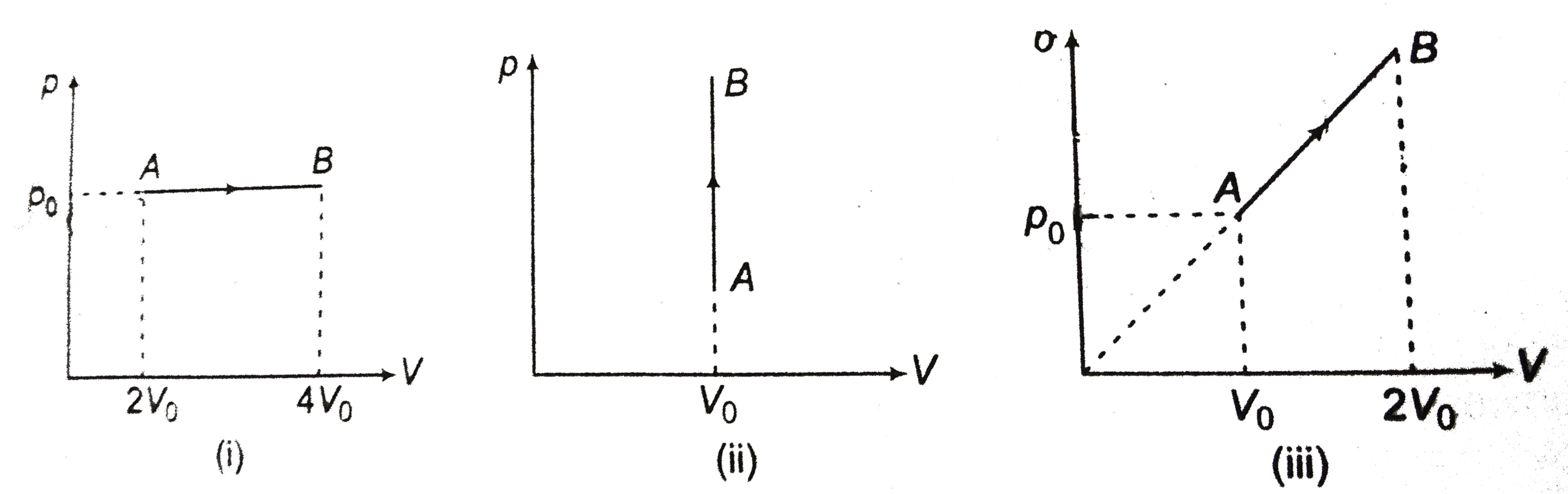 View Solution
View SolutionRefer to figure. Let ΔU1 and ΔU2 be the changes in internal energy in the system in process A+B and ΔW be the net work done by the system in the process A+B,
 View Solution
View SolutionWork done in given cyclic process is
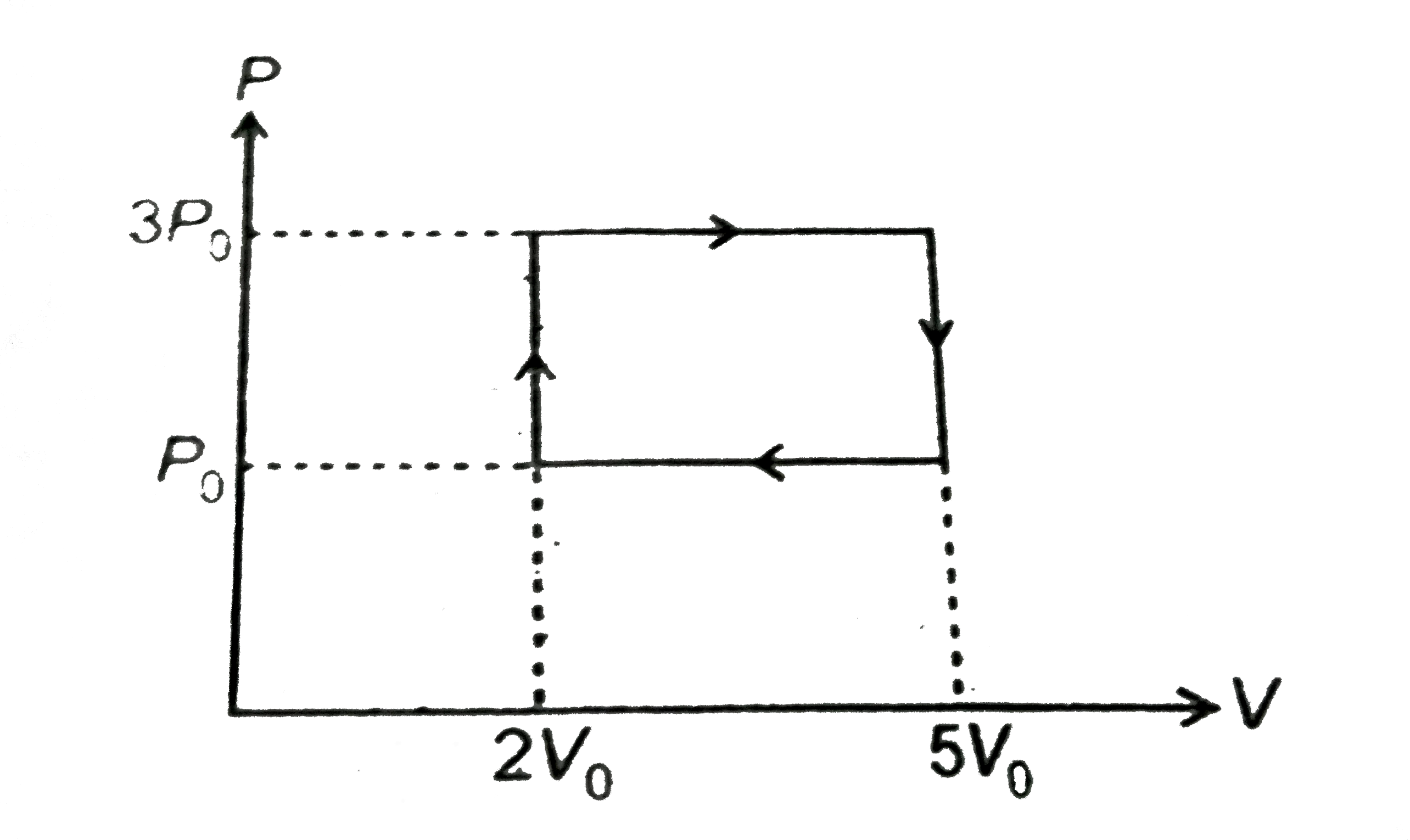 View Solution
View Solutionconsider two processes on a system as shown in fig
the volumes in the initial stage are the same in the two processes and the volume in the final stage are also the same.Let ΔW1andΔW2 be the work done by the system in the processes A and B respectively.
 View Solution
View Solution

