The voltage of a certain cell has standard potential at and are 0.3525 V and 0.3533 V respectively. If the number of electrons involved in te overall reactions are two, calculate and at .
The correct Answer is:
To solve the problem step by step, we will calculate the standard Gibbs free energy change (ΔG°), standard entropy change (ΔS°), and standard enthalpy change (ΔH°) at 25°C using the given standard potentials at two different temperatures.
Step 1: Calculate the change in standard potential (dE/dT)
We know the standard potentials at two temperatures:
- E° at 25°C = 0.3525 V
- E° at 20°C = 0.3533 V
Using the formula for the change in standard potential with temperature:
dEdT=E°25°C−E°20°CT2−T1
Substituting the values:
dEdT=0.3525−0.353325−20=−0.00085=−0.00016V/°C
Step 2: Calculate ΔG° at 25°C
The relationship between Gibbs free energy change and standard potential is given by:
ΔG°=−nFE°
Where:
- n = number of electrons = 2
- F = Faraday's constant = 96500 C/mol
- E° = E° at 25°C = 0.3525 V
Substituting the values:
ΔG°=−2×96500×0.3525=−68.03kJ/mol
Step 3: Calculate ΔS° at 25°C
Using the relationship derived from the Gibbs free energy equation:
ΔG°=ΔH°−TΔS°
We can rearrange it to find ΔS°:
ΔS°=ΔH°−ΔG°T
However, we need ΔH° to calculate ΔS°.
Instead, we can calculate ΔS° directly using the formula:
ΔS°=−dEdT⋅nFT
Substituting the values:
ΔS°=−(−0.00016)⋅2×96500298
Calculating:
ΔS°=0.00016⋅193000298≈0.1kJ/K≈100J/K
Step 4: Calculate ΔH° at 25°C
Now we can use the Gibbs-Helmholtz equation:
ΔH°=ΔG°+TΔS°
Substituting the values:
ΔH°=−68.03+298⋅0.1
Calculating:
ΔH°=−68.03+29.8=−38.23kJ/mol
Final Results
- ΔG° = -68.03 kJ/mol
- ΔS° = 100 J/K (or 0.1 kJ/K)
- ΔH° = -38.23 kJ/mol
- E° at 25°C = 0.3525 V
- E° at 20°C = 0.3533 V
dEdT=E°25°C−E°20°CT2−T1
Substituting the values:
dEdT=0.3525−0.353325−20=−0.00085=−0.00016V/°C
ΔG°=−nFE°
Where:
- n = number of electrons = 2
- F = Faraday's constant = 96500 C/mol
- E° = E° at 25°C = 0.3525 V
ΔG°=−2×96500×0.3525=−68.03kJ/mol
ΔG°=ΔH°−TΔS°
We can rearrange it to find ΔS°:
ΔS°=ΔH°−ΔG°T
However, we need ΔH° to calculate ΔS°.
ΔS°=−dEdT⋅nFT
Substituting the values:
ΔS°=−(−0.00016)⋅2×96500298
Calculating:
ΔS°=0.00016⋅193000298≈0.1kJ/K≈100J/K
ΔH°=ΔG°+TΔS°
Substituting the values:
ΔH°=−68.03+298⋅0.1
Calculating:
ΔH°=−68.03+29.8=−38.23kJ/mol
- ΔS° = 100 J/K (or 0.1 kJ/K)
- ΔH° = -38.23 kJ/mol
Topper's Solved these Questions
- ELECTROCHEMISRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTROCHEMISRYEXERCISE - Assertion Reasoning
11 Videos
- ELECTROCHEMISRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTROCHEMISRYEXERCISE - Subjective Questions
14 Videos
- ELECTROCHEMISRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTROCHEMISRYEXERCISE - Board Level Exercise
20 Videos
- ELECTRO CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO CHEMISTRYEXERCISE - PHYSICAL CHEMITRY (ELECTROCHEMISTRY)
53 Videos
- EQUIVALENT CONCEPT & TITRATIONSBOOK - RESONANCE ENGLISHCHAPTER - EQUIVALENT CONCEPT & TITRATIONSEXERCISE - Part -IV
22 Videos
Similar Questions
Knowledge Check
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
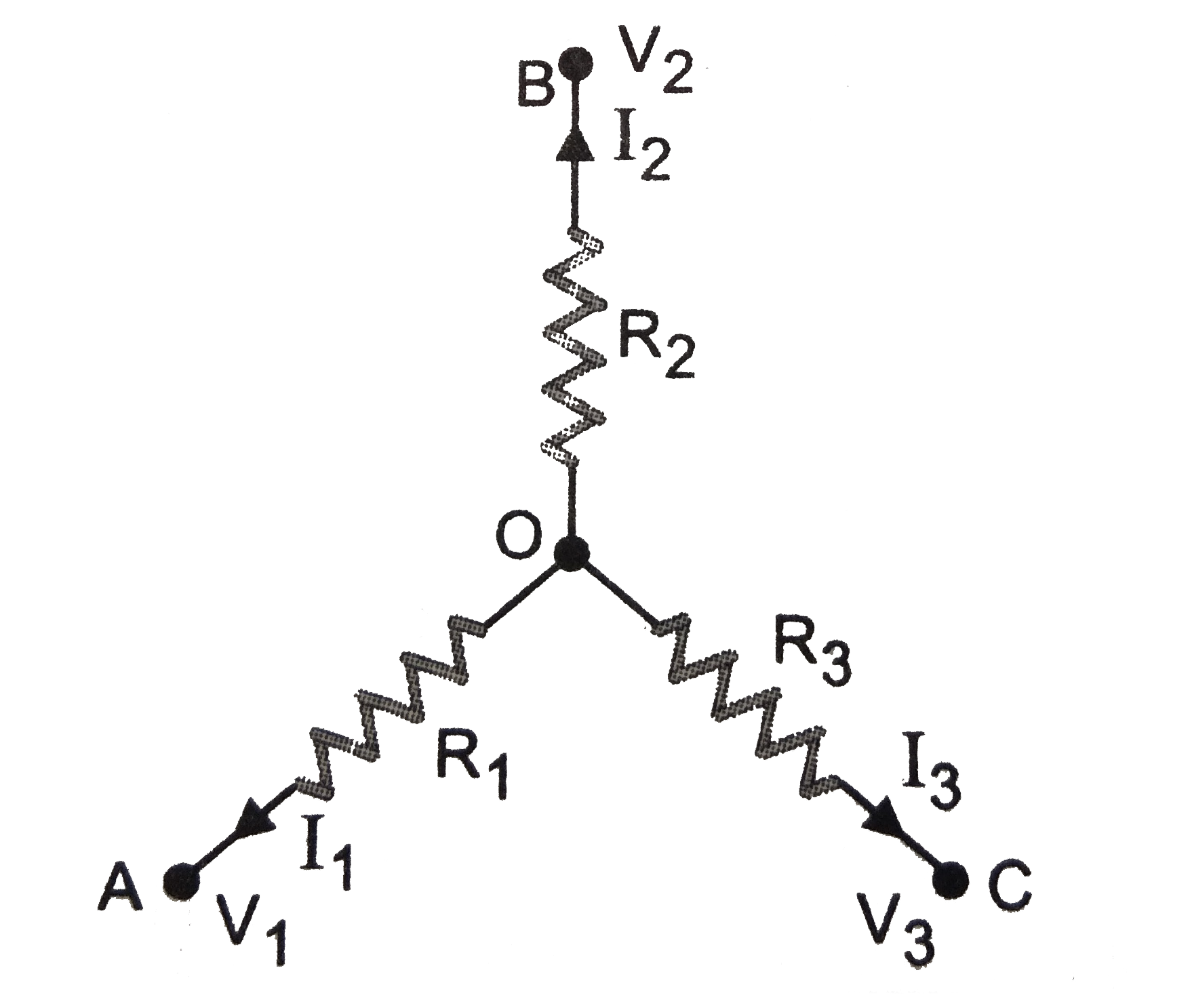 AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)
AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)
The standard electrode potential of four metallic elements (A, B, C and D) are + 0.80, –0.76, + 0.12 and +0.34 V respectively. Arrange them in order of decreasing electropositive character
View SolutionThe standard reduction potentials of two half cells Al3+(aq)∣Aland Mg2+(aq)∣Mg are -1.66V and -2.36V respectively. Calculate the standard cell potential. Write the cell reactions also.
View SolutionCalculate the EMF of a Daniel cell when the concentartion of ZnSO4 and CuSO4 are 0.001M and 0.1M respectively. The standard potential of the cell is 1.1V.
View SolutionThe standard electrode potentials (E∘M+/M) of four metals A, B, C and D are −1.2V,0.6V,0.85Vand−0.76V, respectively. The sequence of deposition of metals on applying potential is
View SolutionThe standard electromitive force of the cell
Fe∣∣Fe2+(aq)∣∣∣∣Cd2+∣∣Cd is 0.0372 V
The temperature coefficient of e.m.f. is −0.125VK−1. Calculate the quantities △G,△H∘ and △S∘ at 25∘C
View SolutionThe gold number of four colloids A, B, C and D are 0.005, 0.08, 25 and 0.10 respectively. Their protective power has the order:
View SolutionE∘ of In3+,In+andCu2+mCu+are−0.4Vand−0.42V respectively, Calculate the equilibrium constant for the reaction. In2++Cu2+→In3++Cu+ at 25∘C.
View Solution
