At normal temprature ,X and Y
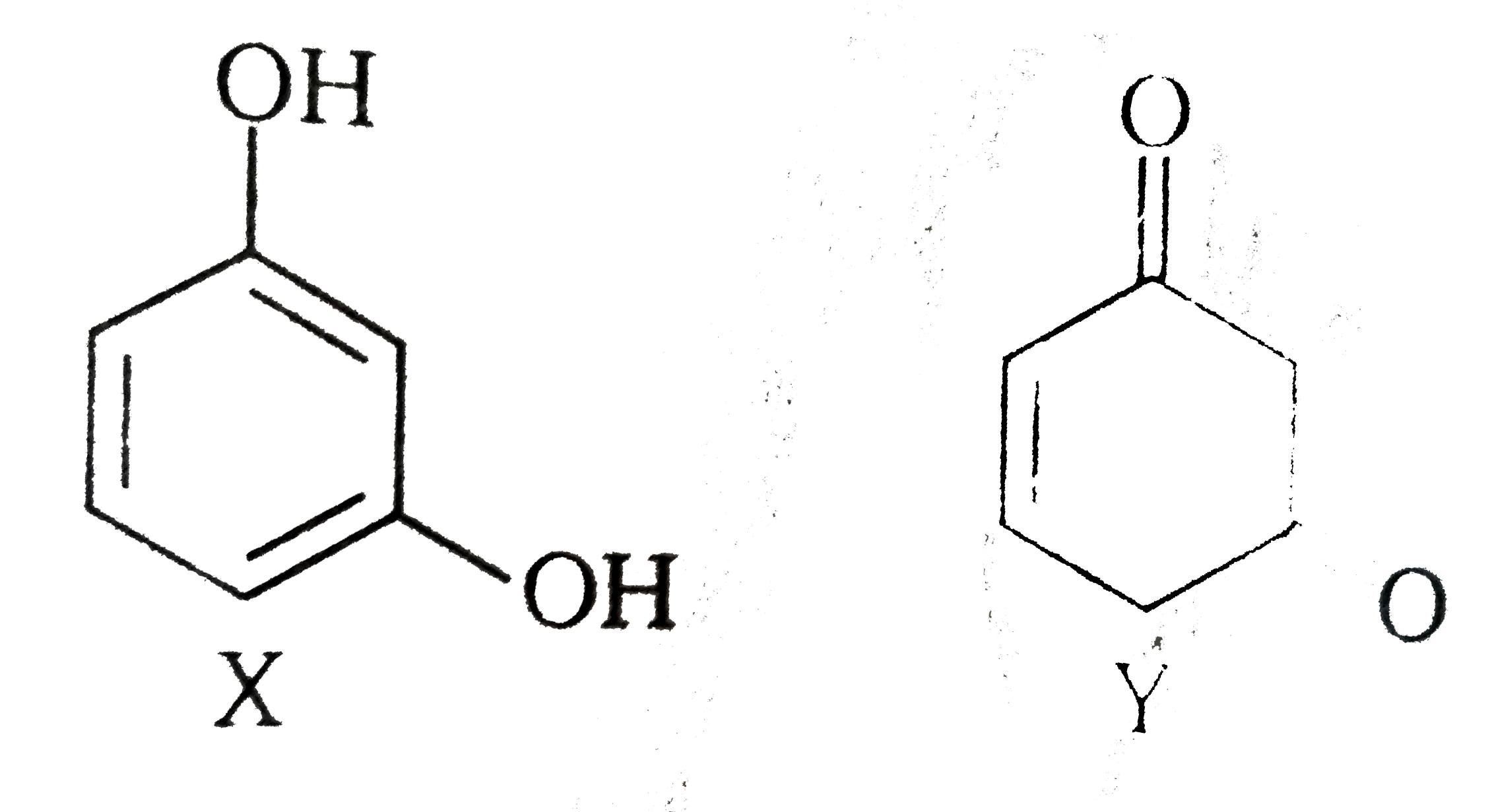
Resonance structures
tautomers
functional isomers
positional isomers
The correct Answer is:B
Step by step video & image solution for At normal temprature ,X and Y by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GENERAL ORGANIC CHEMISTRY IIBook:RESONANCE ENGLISHChapter:GENERAL ORGANIC CHEMISTRY IIExercise:Part-III: Practice Test-2 (IIT-JEE (Advanced Pattern))
Explore 16 Videos
- GENERAL ORGANIC CHEMISTRY IIBook:RESONANCE ENGLISHChapter:GENERAL ORGANIC CHEMISTRY IIExercise:Part-III: Section-4 : Comprehension Type
Explore 3 Videos
- GENERAL ORGANIC CHEMISTRY IIBook:RESONANCE ENGLISHChapter:GENERAL ORGANIC CHEMISTRY IIExercise:(APSP) Part-I:Practice Test-1
Explore 30 Videos
- GASEOUS STATEBook:RESONANCE ENGLISHChapter:GASEOUS STATEExercise:ORGANIC CHEMISTRY(Hydrocarbon)
Explore 18 Videos
- GENERAL ORGANIC CHEMISTRY-IBook:RESONANCE ENGLISHChapter:GENERAL ORGANIC CHEMISTRY-IExercise:PART-III : PRACTICE TEST-19
Explore 1 Video
Similar Questions
Knowledge Check
The equation of the normal to the curve y=sinx at (0,0) is
Ay = 0Bx = 0Cx + y = 0Dx - y = 0
The equation to the normal to the curve y=sinx at (0, 0) is
(a)x=0
(b) y=0
(c) x+y=0
(d) x−y=0
View SolutionThree normals are drawn from the point (14,7) to the curve y2−16x−8y=0. Find the coordinates of the feet of the normals.
View SolutionFind the equations of the tangent and the normal to the curve y2=4ax at (x1, y1) at indicated points.
View SolutionThe normal at the point (1,1) on the curve 2y+x2=3is
(A) x−y=0
(B) xy=0
(C) x+y+1=0
(D) xy=0
View SolutionThe normal at the point (1,1) on the curve 2y+x2=3is
(A) x+y=0
(B) xy=0
(C) x+y+1=0
(D) xy=0
View SolutionFind the slopes of the tangent and the normal to the curve xy=6 at (1, 6)
View SolutionThe length of normal at any point to the curve, y=ccosh(xc) is
View Solution