Let A={p,q,r}. Which of the following is an equivalence relation on A? (a) R1={(p,q),(q,r),(p,r),(p,q)} (b) R2={(r,q),(r,p),(r.r),(q,r)} (c) R3={(p,p),(q,q),(r,r),(p,q)} (d) one of these
The correct Answer is:(i) Reflexive and transitive but not symmetric.
To determine which of the given relations is an equivalence relation on the set A={p,q,r}, we need to check each relation for three properties: reflexivity, symmetry, and transitivity.
1. Check Relation R1={(p,q),(q,r),(p,r),(p,q)}
- Reflexivity: A relation is reflexive if every element is related to itself. Here, we need (p,p),(q,q),(r,r) to be present in R1. Since none of these pairs are present, R1 is not reflexive.
- Symmetry: A relation is symmetric if whenever (a,b) is in the relation, (b,a) must also be in the relation. Here, (p,q) is in R1 but (q,p) is not. Thus, R1 is not symmetric.
- Transitivity: A relation is transitive if whenever (a,b) and (b,c) are in the relation, then (a,c) must also be in the relation. Here, (p,q) and (q,r) are in R1, but (p,r) is already included. However, since it fails reflexivity and symmetry, we can conclude that R1 is not an equivalence relation.
2. Check Relation R2={(r,q),(r,p),(r,r),(q,r)}
- Reflexivity: For R2 to be reflexive, we need (p,p),(q,q),(r,r). Here, (r,r) is present, but (p,p) and (q,q) are not. Thus, R2 is not reflexive.
- Symmetry: The pair (r,q) is in R2 but (q,r) is also present, which satisfies symmetry for this pair. However, (r,p) is in R2 but (p,r) is not. Thus, R2 is not symmetric.
- Transitivity: We can check pairs, but since it fails reflexivity and symmetry, we conclude that R2 is not an equivalence relation.
3. Check Relation R3={(p,p),(q,q),(r,r),(p,q)}
- Reflexivity: All elements p,q,r are related to themselves: (p,p),(q,q),(r,r) are present. Thus, R3 is reflexive.
- Symmetry: The pair (p,q) is in R3, but (q,p) is not. Thus, R3 is not symmetric.
- Transitivity: Since it is not symmetric, we do not need to check transitivity. Therefore, R3 is not an equivalence relation.
4. Conclusion: Since none of the relations R1,R2, or R3 satisfy all three properties of an equivalence relation, the answer is (d) none of these.
- Symmetry: A relation is symmetric if whenever (a,b) is in the relation, (b,a) must also be in the relation. Here, (p,q) is in R1 but (q,p) is not. Thus, R1 is not symmetric.
- Transitivity: A relation is transitive if whenever (a,b) and (b,c) are in the relation, then (a,c) must also be in the relation. Here, (p,q) and (q,r) are in R1, but (p,r) is already included. However, since it fails reflexivity and symmetry, we can conclude that R1 is not an equivalence relation.
- Symmetry: The pair (r,q) is in R2 but (q,r) is also present, which satisfies symmetry for this pair. However, (r,p) is in R2 but (p,r) is not. Thus, R2 is not symmetric.
- Transitivity: We can check pairs, but since it fails reflexivity and symmetry, we conclude that R2 is not an equivalence relation.
- Symmetry: The pair (p,q) is in R3, but (q,p) is not. Thus, R3 is not symmetric.
- Transitivity: Since it is not symmetric, we do not need to check transitivity. Therefore, R3 is not an equivalence relation.
Topper's Solved these Questions
- RELATION, FUNCTION & ITFBOOK - RESONANCE ENGLISHCHAPTER - RELATION, FUNCTION & ITFEXERCISE - SCQ_TYPE
96 Videos
- RELATION, FUNCTION & ITFBOOK - RESONANCE ENGLISHCHAPTER - RELATION, FUNCTION & ITFEXERCISE - MATCH THE COLUMN
2 Videos
- RELATION, FUNCTION & ITFBOOK - RESONANCE ENGLISHCHAPTER - RELATION, FUNCTION & ITFEXERCISE - SSP
55 Videos
- NUMBER THEORYBOOK - RESONANCE ENGLISHCHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)
4 Videos
- SEQUENCE & SERIES BOOK - RESONANCE ENGLISHCHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)
3 Videos
Similar Questions
Knowledge Check
Δ=∣∣ ∣ ∣∣pqrp+2aq+2br+2cabc∣∣ ∣ ∣∣ then
Aa) Δ=0Bb) Δ=abcCc) Δ=pqrDd) None of these
Let p,qandr be three statements, then (~p→q)→r is equivalent to
View SolutionIf A={a,b, c,d}, B={p,q,r,s} than Is the following relation from A → B? Give reasons for your answer.: R3={(a,p), (a,q), (d,p), (c,r), (b,r)}
View Solution.1p+q,1q+r,1r+p are in AP, then
View SolutionConstruct the truth table for the followings statements :
(a) (p∧q)→~p (b)(p∧q)→(p∨q)
(c) (p∧q)→r (d)[p∧(~r)]→(q∨r)
View SolutionWithout expanding the determinant prove that: ∣∣ ∣ ∣∣0p−qp−rq−p0q−rr−pr−q0∣∣ ∣ ∣∣=0
View SolutionThe mean of is same as the mean of Then which of the following is correct? p=q=r (b) q=r=s q=r (d) p=r+s
View SolutionMatch the columns and choose correct options.
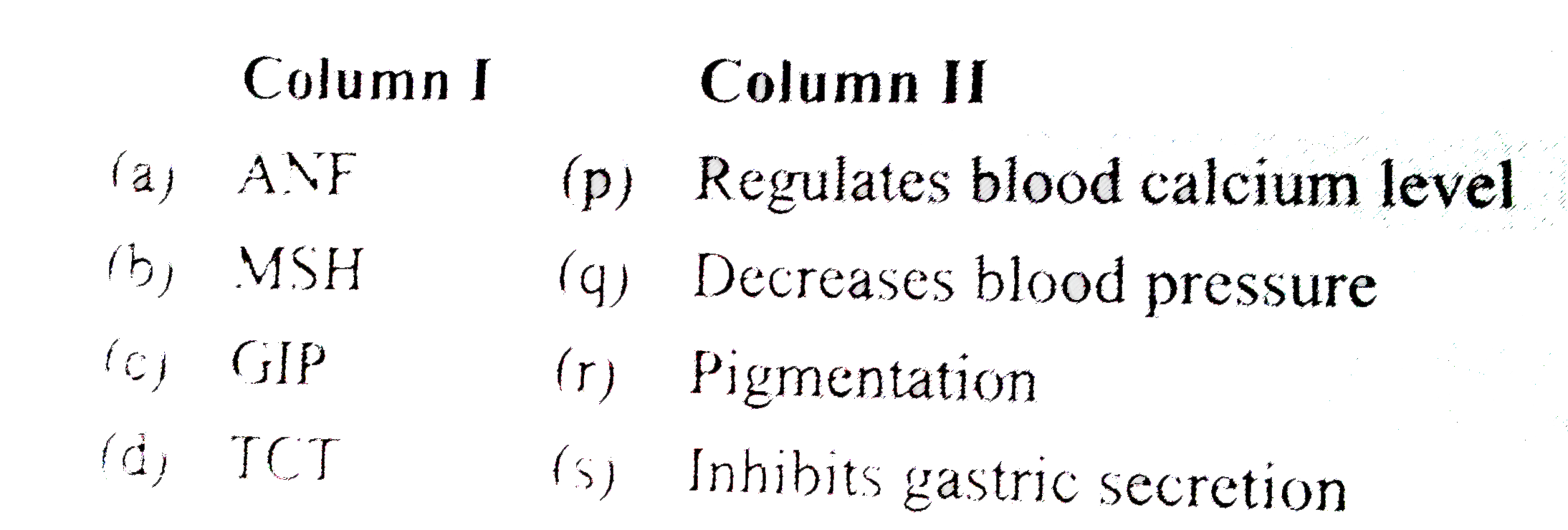
(1) a-q, b-r, c-s, d-p
(2) a-s, b-p, c-q, d-r
(3) a-q, b-p, c-s, d-r
(4) a-s, b-p, c-r, d-q
View Solution