Statement -1 All points of intersection of y=f(x) and y=f−1(x) lies on y=x only.
Statement -2 If point P(α,β) lies on y=f(x) then Q(β,α) lies on y=f−1(x).
Statement -3 Inverse of invertible function is unique and its range is equal to the function domain.
Which of the following option is correct for above statements in order
a.TTF
b.FTT
c.TTT
d.TFT
The correct Answer is:C
To analyze the statements provided in the question, we will evaluate each statement step by step.
Step 1: Evaluate Statement 1
Statement 1: All points of intersection of y=f(x) and y=f−1(x) lie on y=x only.
Solution:
To find the points of intersection between the two functions, we set them equal to each other:
f(x)=f−1(x)
If we let y=f(x), then by the definition of the inverse function, we have:
f(f−1(x))=x
This implies that if f(x)=y, then f−1(y)=x. Thus, if f(x)=f−1(x), we can replace f−1(x) with y:
f(x)=x
This means that the points of intersection must lie on the line y=x. Therefore, Statement 1 is correct.
Step 2: Evaluate Statement 2
Statement 2: If point P(α,β) lies on y=f(x), then Q(β,α) lies on y=f−1(x).
Solution:
Given that point P(α,β) lies on y=f(x), we have:
f(α)=β
To find if Q(β,α) lies on y=f−1(x), we need to check if:
f−1(β)=α
By the definition of the inverse function, if f(α)=β, then:
f−1(β)=α
This confirms that point Q(β,α) indeed lies on y=f−1(x). Therefore, Statement 2 is correct.
Step 3: Evaluate Statement 3
Statement 3: The inverse of an invertible function is unique and its range is equal to the function's domain.
Solution:
This statement is a fundamental property of invertible functions. If a function f is invertible, it means that for every output y in the range of f, there is a unique input x in the domain such that f(x)=y. Thus, the inverse function f−1 is unique and its range (the set of possible outputs) is equal to the domain of the original function f. Therefore, Statement 3 is correct.
Conclusion
All three statements are correct. Thus, the correct option is:
- C: All statements are correct.
Statement 1: All points of intersection of y=f(x) and y=f−1(x) lie on y=x only.
To find the points of intersection between the two functions, we set them equal to each other:
f(x)=f−1(x)
If we let y=f(x), then by the definition of the inverse function, we have:
f(f−1(x))=x
This implies that if f(x)=y, then f−1(y)=x. Thus, if f(x)=f−1(x), we can replace f−1(x) with y:
f(x)=x
This means that the points of intersection must lie on the line y=x. Therefore, Statement 1 is correct.
Statement 2: If point P(α,β) lies on y=f(x), then Q(β,α) lies on y=f−1(x).
Given that point P(α,β) lies on y=f(x), we have:
f(α)=β
To find if Q(β,α) lies on y=f−1(x), we need to check if:
f−1(β)=α
By the definition of the inverse function, if f(α)=β, then:
f−1(β)=α
This confirms that point Q(β,α) indeed lies on y=f−1(x). Therefore, Statement 2 is correct.
Statement 3: The inverse of an invertible function is unique and its range is equal to the function's domain.
This statement is a fundamental property of invertible functions. If a function f is invertible, it means that for every output y in the range of f, there is a unique input x in the domain such that f(x)=y. Thus, the inverse function f−1 is unique and its range (the set of possible outputs) is equal to the domain of the original function f. Therefore, Statement 3 is correct.
All three statements are correct. Thus, the correct option is:
- C: All statements are correct.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - RELATION, FUNCTION & ITFEXERCISE - MATCH THE COLUMN2videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCE ENGLISHCHAPTER - RELATION, FUNCTION & ITFEXERCISE - INTEGER_TYPE21videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCE ENGLISHCHAPTER - RELATION, FUNCTION & ITFEXERCISE - SUBJECTIVE_TYPE179videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCE ENGLISHCHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)4videos
NUMBER THEORY
- BOOK - RESONANCE ENGLISHCHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)3videos
SEQUENCE & SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
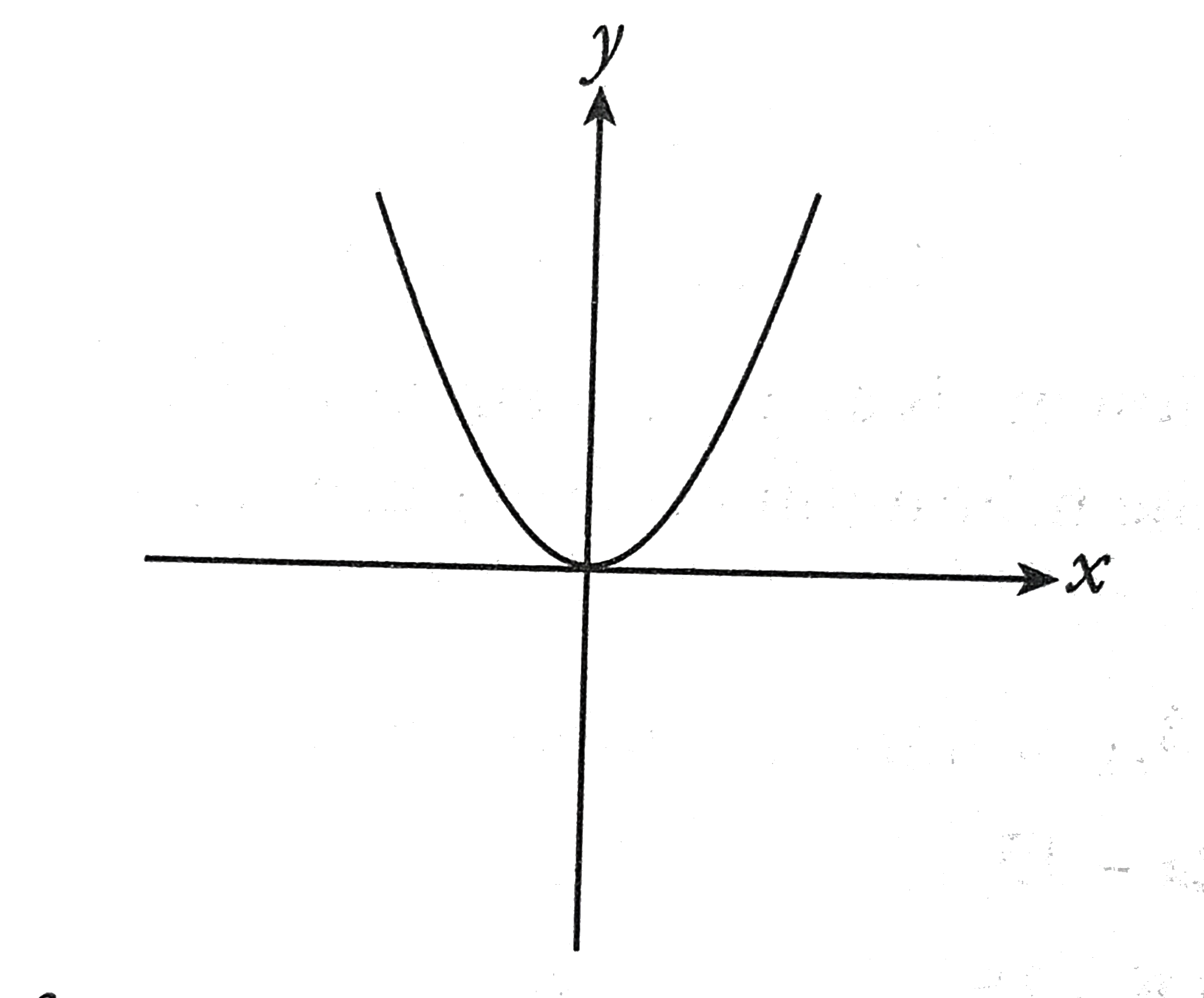
The quadratic y=f(x) is shown above. Which of the following graphs represents the function y=f(x+3)−4?A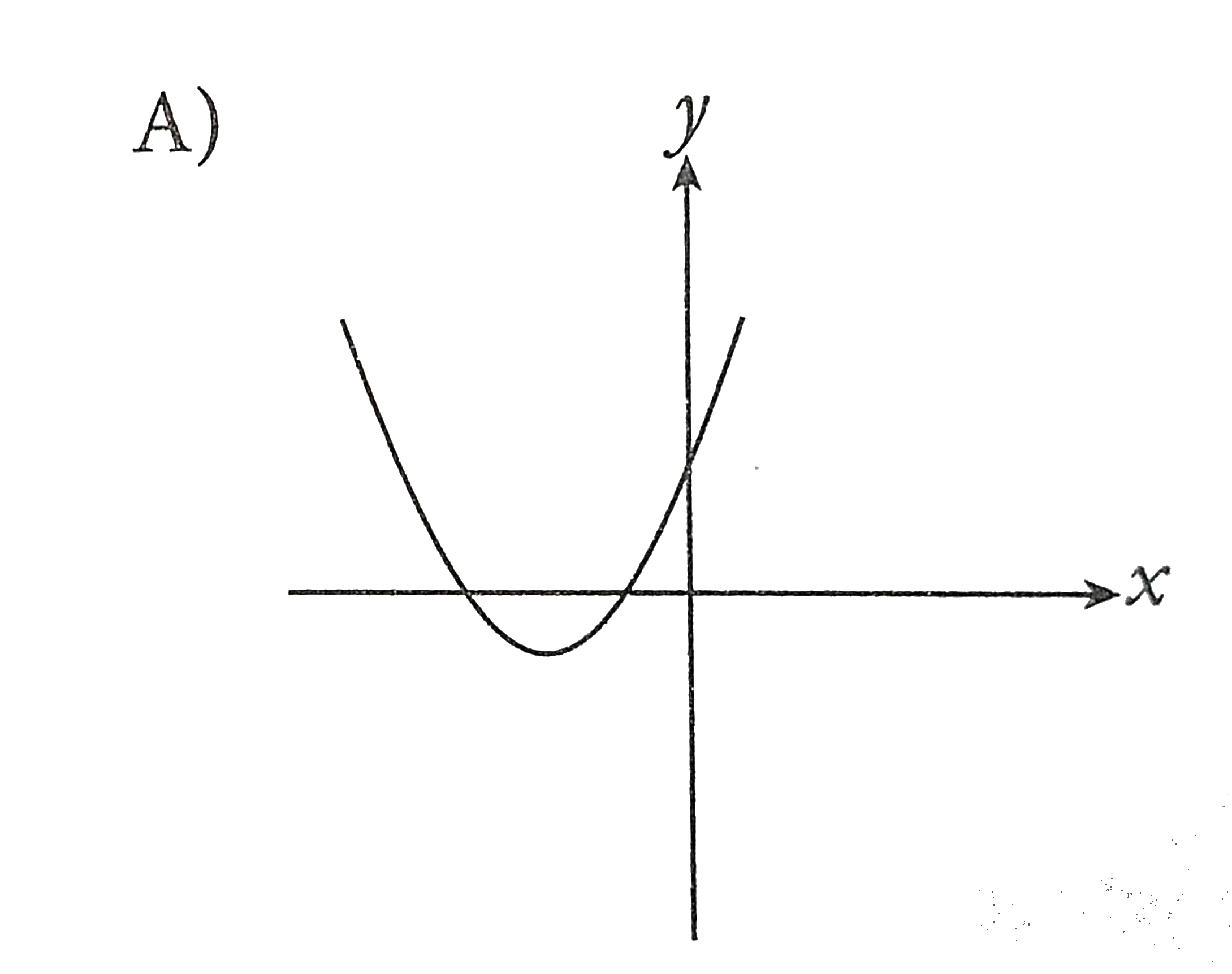 B
B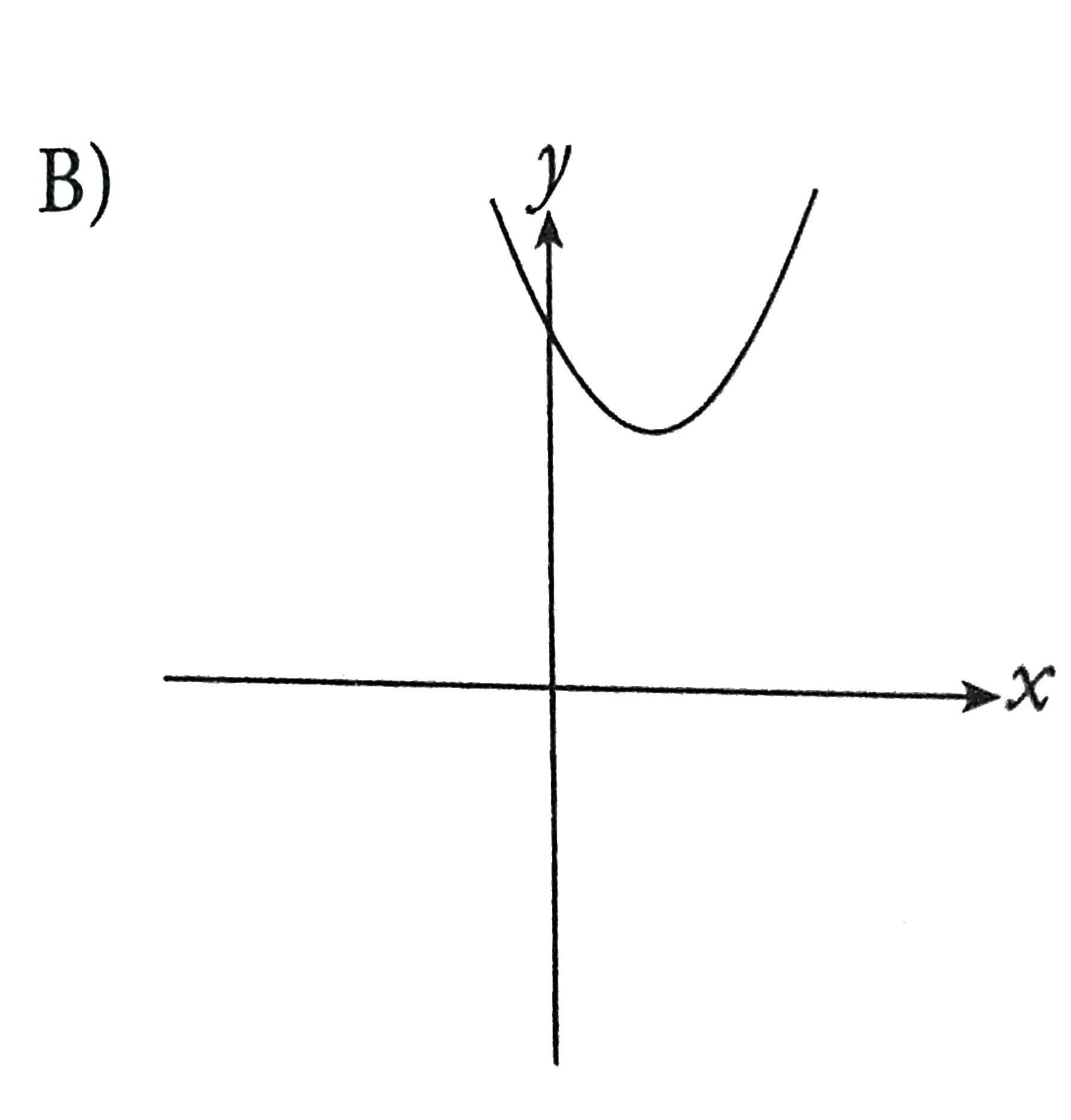 C
C D
D
The graph of the function y=f(x) is shown in the adjacent figure then correct statement is
 View Solution
View SolutionI If a point (α,β) lies on the circle x2+y2=1 then the locus of the point (3α.+2,β), is
View SolutionStatement-1 : f(x) is a one-one function ⇔f−1(x) is a one-one function.
and
Statement-2 f−1(x) is the reflection of the function f(x) with respect to y = x.View SolutionStatement-1 If y=f(x) is increasing in [α,β], then its range is [f(α),f(β)]
Statement-2 Every increasing function need not to be continuous.View SolutionIf point P(α,α2−2) lies inside the triangle formed by the lines x+y=1,y=x+1andy=−1 then α∈
View Solutiony = f(x) be a real valued function with domain as all real numbers. If the graph of the function is symmetrical about the line x = 1, then for all α∈R
View SolutionStatement-1: Reflection of the point (-3, 2) in the line x + y = 0 is (-2, 3).Statement-2: The reflection of a point P(α,β) in the line ax+by+c=0 is the point Q(α',β')if (α+α'2,β+β'2) lies on the line
View Solution
