The area of parallel plates of an air capacitor is 0.2m2 and the distance between them is 0.01m The potential difference between the plates, the potential difference between the plates is 3000V. When a 0.01m thick sheet of an insulating material is placed between the plates, the potential difference decrease to 1000 volt. Determine (i) capacitance of capacitance before placing the sheet (ii) charge on each plate (iii) dielectric constant of material (iv) capacitanc after placing the insulator (v) absoulate permittivity of the dielectric.
The correct Answer is:(i)20∈0=180pF (ii)5.4×10−7C
(iii)540pF (iv)3
(v)27×10−12C2N−1m−2 (vi)3×105V/m
(vii)1×105V/m
To solve the problem step by step, let's break down each part of the question systematically.
Given Data:
- Area of the plates, A=0.2m2
- Distance between the plates, d=0.01m
- Initial potential difference, V1=3000V
- Potential difference after inserting the dielectric, V2=1000V
- Thickness of the dielectric sheet, ddielectric=0.01m
Part (i): Capacitance before placing the sheet
The formula for the capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
Where:
- ε0 (the permittivity of free space) is approximately 8.85×10−12F/m.
Substituting the values:
C=(8.85×10−12F/m)×(0.2m2)0.01m
Calculating:
C=(8.85×10−12)×(0.2)0.01=1.77×10−10F=17.7×10−11F
Part (ii): Charge on each plate
The charge Q on each plate can be calculated using the formula:
Q=C×V
Substituting the values:
Q=(1.77×10−10F)×(3000V)
Calculating:
Q=5.31×10−7C=53.1×10−8C
Part (iii): Dielectric constant of the material
The dielectric constant K can be found using the relationship between the initial and final potential differences:
K=V1V2
Substituting the values:
K=3000V1000V=3
Part (iv): Capacitance after placing the insulator
The capacitance with the dielectric inserted is given by:
C′=ε0KAd
Substituting the values:
C′=(8.85×10−12F/m)×3×(0.2m2)0.01m
Calculating:
C′=(8.85×10−12)×3×(0.2)0.01=5.31×10−10F=53.1×10−11F
Part (v): Absolute permittivity of the dielectric
The absolute permittivity ε of the dielectric material is given by:
ε=ε0K
Substituting the values:
ε=(8.85×10−12F/m)×3
Calculating:
ε=2.655×10−11F/m=26.55×10−12F/m
Summary of Results:
1. Capacitance before placing the sheet: C=17.7×10−11F
2. Charge on each plate: Q=53.1×10−8C
3. Dielectric constant: K=3
4. Capacitance after placing the insulator: C′=53.1×10−11F
5. Absolute permittivity of the dielectric: ε=26.55×10−12F/m
- Area of the plates, A=0.2m2
- Distance between the plates, d=0.01m
- Initial potential difference, V1=3000V
- Potential difference after inserting the dielectric, V2=1000V
- Thickness of the dielectric sheet, ddielectric=0.01m
- ε0 (the permittivity of free space) is approximately 8.85×10−12F/m.
1. Capacitance before placing the sheet: C=17.7×10−11F
2. Charge on each plate: Q=53.1×10−8C
3. Dielectric constant: K=3
4. Capacitance after placing the insulator: C′=53.1×10−11F
5. Absolute permittivity of the dielectric: ε=26.55×10−12F/m
Topper's Solved these Questions
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 2
74 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 3
26 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example
3 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
Similar Questions
In a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View Solution
Knowledge Check
In the question number 7, the rate of change of potential difference between the plates is
A2.41×109Vs−1B1.87×109Vs−1C3.2×10−4Vs−1D4.5×10−4Vs−1
A parallel plate air capacitor has capcity C distance of separtion between plates is d and potential difference V is applied between the plates force of attraction between the plates of the parallel plate air capacitor is
View SolutionIn a parallel plate capacitor, the distance between the plates is d and potential difference across the plate is V. Energy stored per unit volume between the plates of capacitor is
View SolutionTwo large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. Potential difference between points X and Y as indicated in the figure will be
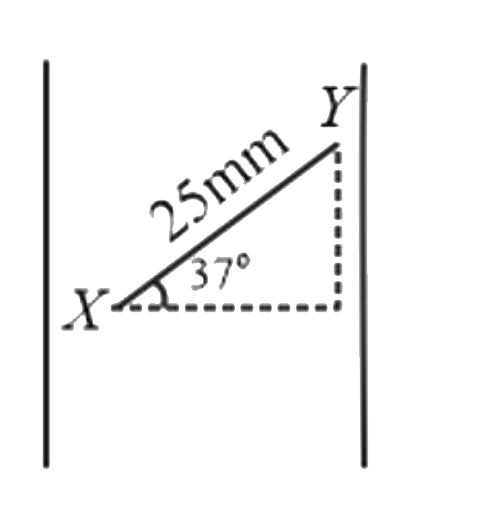
View SolutionTwo parallel conducting plates of a capacitor of capacitance C containing charges Q and -2Q at a distance d apart. Find out potential difference between the plates of capacitors.
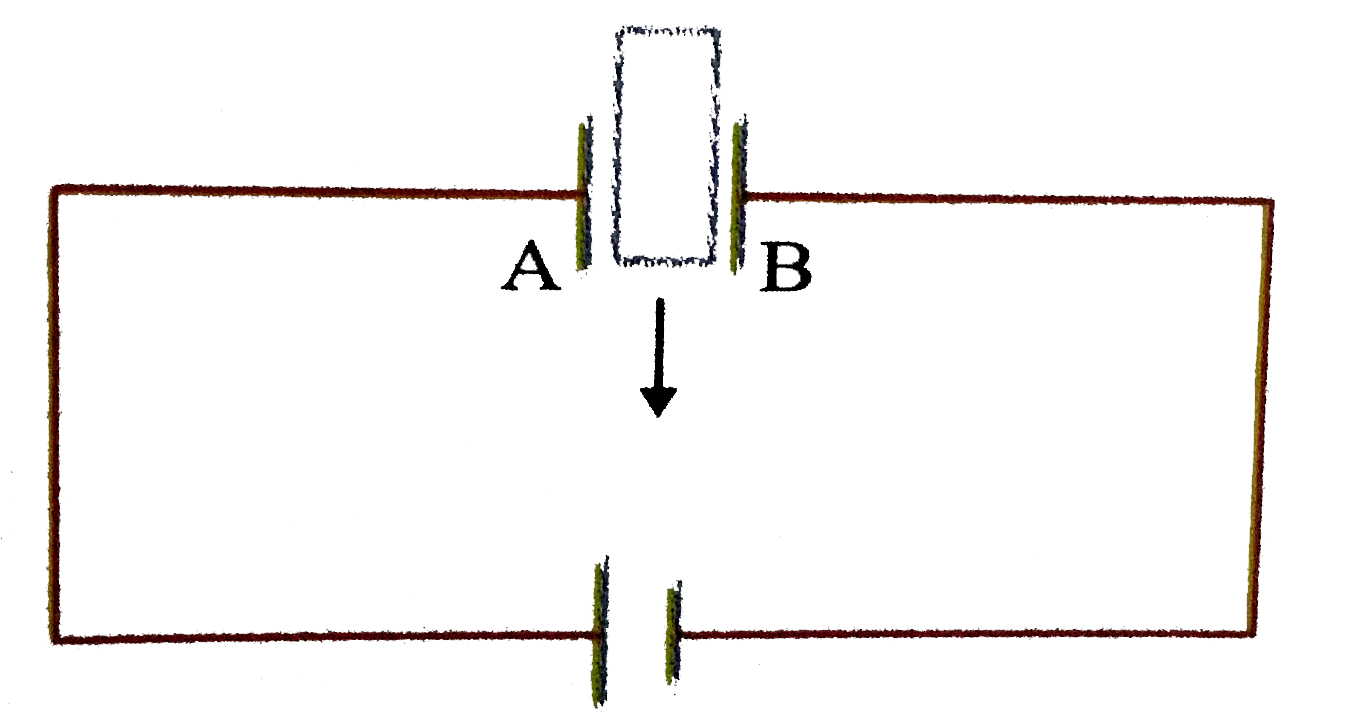
View SolutionAn insulator plate is passed between the plates of a capacitor. Then current
 .
.
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time.After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionA 5.80μF parallel-plate air capacitor has a plate separation of 5.00mm and is charged to a potential difference of 400V. Calculate the energy density in the region between the plates, in Jm3
View Solution
