A 3 mega ohm resistor and an uncharged 1μF capacitor are connected in a single loop circuit with a constant source of 4 volt. At one second after the connection is made what are the rates at which,
(iii) Joule heat is appearing in the resistor.
163e−1/3μJ/s
12e−1/3μJ/s
163(e−2/3)μJ/s
163(1−e−1/3)2μJ/s
The correct Answer is:C
To solve the problem of finding the rate at which Joule heat is appearing in the resistor at one second after the connection is made, we can follow these steps:
Step 1: Identify the components and their values
We have:
- Resistor (R) = 3 mega ohms = 3×106Ω
- Capacitor (C) = 1 microfarad = 1×10−6F
- Voltage (E) = 4 volts
Step 2: Write the Kirchhoff's loop law equation
According to Kirchhoff's loop law, we can write the equation for the circuit as:
E−IR−QC=0
Where:
- I is the current,
- Q is the charge on the capacitor.
Step 3: Relate current and charge
The current I can be expressed as:
I=dQdt
Substituting this into the loop equation gives:
E−RdQdt−QC=0
Step 4: Rearranging the equation
Rearranging the equation, we get:
RdQdt=E−QC
Step 5: Solve the differential equation
To solve this, we can separate variables:
dQE−QC=dtR
Integrating both sides will give us the relationship between charge Q and time t.
Step 6: Find the maximum current
The maximum current I0 in the circuit when the capacitor is uncharged is given by:
I0=ER=43×106A
Step 7: Current as a function of time
The current I(t) at time t can be expressed as:
I(t)=I0e−tRC
Where RC is the time constant of the circuit:
RC=(3×106)×(1×10−6)=3seconds
Thus,
I(t)=43×106e−t3
Step 8: Calculate the current at t=1 second
Substituting t=1 second into the equation:
I(1)=43×106e−13
Step 9: Calculate the power (Joule heat) in the resistor
The power P (rate of Joule heat) in the resistor is given by:
P=I2R
Substituting I(1) into this equation:
P=(43×106e−13)2×(3×106)
Step 10: Simplify the expression
Calculating this gives:
P=16(3×106)2e−23×(3×106)
P=163×106e−23
Final Result
The rate at which Joule heat is appearing in the resistor at t=1 second is:
P=163e−23watts
We have:
- Resistor (R) = 3 mega ohms = 3×106Ω
- Capacitor (C) = 1 microfarad = 1×10−6F
- Voltage (E) = 4 volts
According to Kirchhoff's loop law, we can write the equation for the circuit as:
E−IR−QC=0
Where:
- I is the current,
- Q is the charge on the capacitor.
The current I can be expressed as:
I=dQdt
Substituting this into the loop equation gives:
E−RdQdt−QC=0
Rearranging the equation, we get:
RdQdt=E−QC
To solve this, we can separate variables:
dQE−QC=dtR
Integrating both sides will give us the relationship between charge Q and time t.
The maximum current I0 in the circuit when the capacitor is uncharged is given by:
I0=ER=43×106A
The current I(t) at time t can be expressed as:
I(t)=I0e−tRC
Where RC is the time constant of the circuit:
RC=(3×106)×(1×10−6)=3seconds
Thus,
I(t)=43×106e−t3
Substituting t=1 second into the equation:
I(1)=43×106e−13
The power P (rate of Joule heat) in the resistor is given by:
P=I2R
Substituting I(1) into this equation:
P=(43×106e−13)2×(3×106)
Calculating this gives:
P=16(3×106)2e−23×(3×106)
P=163×106e−23
The rate at which Joule heat is appearing in the resistor at t=1 second is:
P=163e−23watts
Topper's Solved these Questions
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 2
74 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 3
26 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example
3 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
Similar Questions
A 3 mega ohm resistor and an uncharged 1μF capacitor are connected in a single loop circuit with a constant source of 4 volt. At one second after the connection is made what are the rates at which,
(ii) Energy is being stored in the capacitor.
View SolutionA 3 mega ohm resistor and an uncharged 1μF capacitor are connected in a single loop circuit with a constant source of 4 volt. At one second after the connection is made what are the rates at which,
(iv) Energy is being delivered by the source.
View Solution
Knowledge Check
A 0.2kΩ resistor and 15μF capacitor are connected in series to a 220 V, 50 Hz ac source. The impadance of the circuit is
A250ΩB268ΩC29.15ΩD291.5Ω
A 3 mega ohm resistor and an uncharged 1μF capacitor are connected in a single loop circuit with a constant source of 4 volt. At one second after the connection is made what are the rates at which,
(i) The charge on the capacitor is increasing.
View SolutionA 400 Ω resistor, a 3 H inductor and a 5 μF capacitor are connected in series to a 220 V, 50 Hz ac source. Calculate the :
(1) Impedance of the ciruit.
(ii) Current flowing through the circuit.
View SolutionThe plates of a 50(μ)F capacitor charged to 400(μ)C are connected through a resistance of 1.0k(ohm). Find the charge remaining on the capacitor 1s after the connection is made.
View SolutionA condenser of capacity 1 μ F and a resistance 0.5 mega-ohm are connected in series with a DC supply of 2 V. The time constant of circuit is
View SolutionA capacitor of capacitance 2.0μF is charged to a potential difference of 12 V. It is then connected to an uncharged capacitor of capacitance 4.0μF. Find (a) the charge flow through connecting wire upto study strate on each of the two capacitors after the connection in μC (b) The total electrostatic energy stored in both capacitors in μJ (c) the heat produced during the charge transfer from one capacitor to the other in μJ.
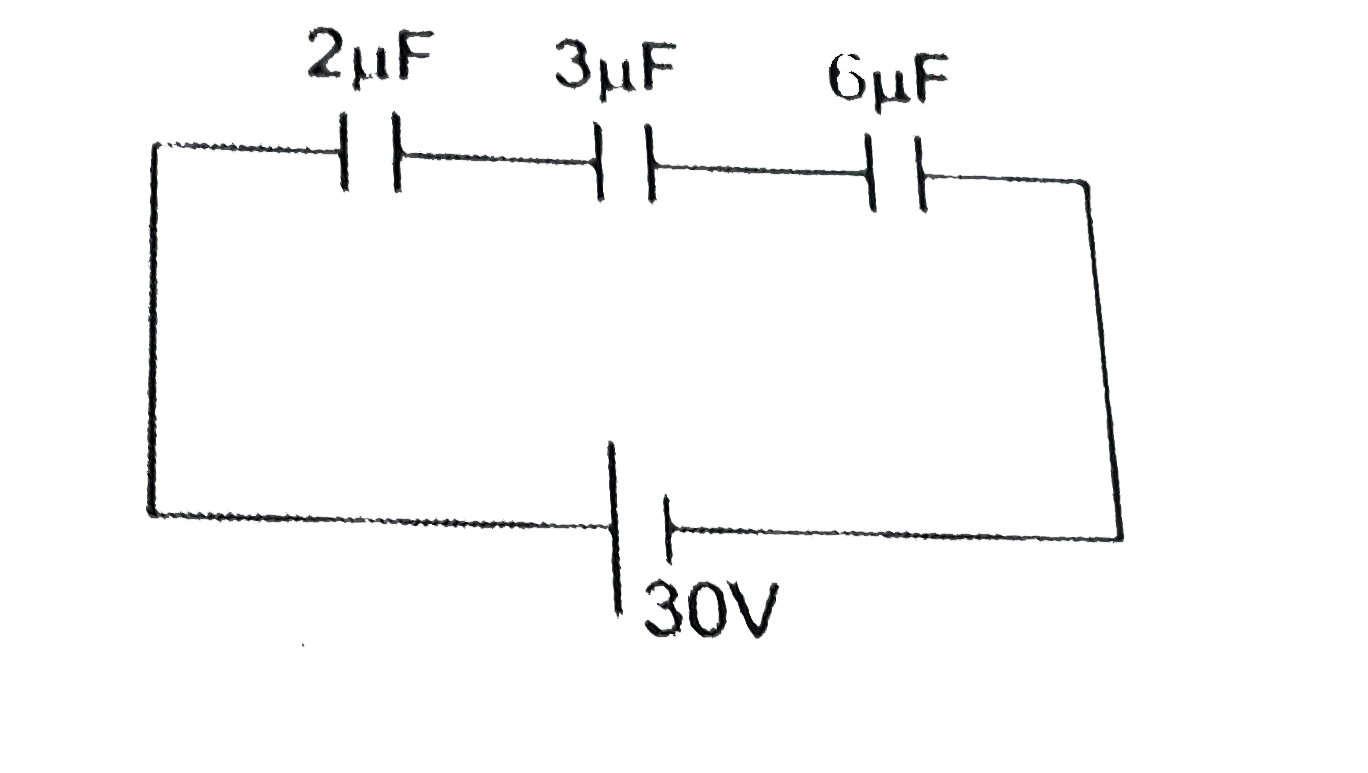
View SolutionThree initially uncharged capacitors are connected in series as shown in circuit with a battery of emf 30V. Find out following :
(i) charge flow through the battery,
(ii) potential energy in 3μF capacitor.
(iii) Utotal in capacitors
(iv) heat produced in the circuit
View SolutionA fresh dry cell of 1.5 volt and two resistors of 10kΩ each are connected in series. An analog voltmeter measures a voltage of 0.5 volt across each of the resistor. A 100μF capacitor is fully charged using the same source. The same voltmeter is now used to measure the voltage across It. The initial value of the current and the time in which the voltmeter reading falls to 0.5 volt are respectively.
View Solution
