Two identical non-conducting spherical shells having equal charge Q, which is uniformly distributed on it, are placed at a distance d apart. From where they are released.Find out kinetic energy of each sphere when they are at a large distance.
The correct Answer is:
To solve the problem, we need to find the kinetic energy of each of the two identical non-conducting spherical shells with charge Q when they are at a large distance apart after being released from an initial separation of distance d.
1. Understand the System:
- We have two identical non-conducting spherical shells, each with charge Q, placed at a distance d apart.
- The charges are uniformly distributed on each shell.
2. Calculate Initial Potential Energy:
- The potential energy (U) of the system when the shells are at distance d can be calculated using the formula for the potential energy of two point charges:
U=kQ2d
- Here, k is the Coulomb's constant.
3. Consider Self-Energy:
- Each shell also has its own self-energy, which can be calculated using the formula:
Uself=kQ22R
- Since there are two shells, the total self-energy is:
Uself total=2⋅kQ22R=kQ2R
4. Total Initial Potential Energy:
- The total initial potential energy of the system when the shells are at distance d is:
Uinitial=U+Uself total=kQ2d+kQ2R
5. Final Potential Energy at Large Distance:
- When the shells are at a large distance apart, the potential energy approaches zero because the interaction between the charges diminishes.
- The final potential energy Ufinal=0.
6. Apply Conservation of Energy:
- According to the law of conservation of energy:
Initial Kinetic Energy+Initial Potential Energy=Final Kinetic Energy+Final Potential Energy
- Initially, the kinetic energy is zero (the shells are at rest), so we have:
0+Uinitial=Kfinal+0
- Therefore, the final kinetic energy of the system (K) is equal to the initial potential energy:
K=Uinitial=kQ2d+kQ2R
7. Distributing Kinetic Energy:
- Since the kinetic energy is shared equally between the two shells, the kinetic energy of each shell Keach is:
Keach=K2=12(kQ2d+kQ2R)
Final Answer:
The kinetic energy of each sphere when they are at a large distance apart is:
Keach=12(kQ2d+kQ2R)
- We have two identical non-conducting spherical shells, each with charge Q, placed at a distance d apart.
- The charges are uniformly distributed on each shell.
- The potential energy (U) of the system when the shells are at distance d can be calculated using the formula for the potential energy of two point charges:
U=kQ2d
- Here, k is the Coulomb's constant.
- Each shell also has its own self-energy, which can be calculated using the formula:
Uself=kQ22R
- Since there are two shells, the total self-energy is:
Uself total=2⋅kQ22R=kQ2R
- The total initial potential energy of the system when the shells are at distance d is:
Uinitial=U+Uself total=kQ2d+kQ2R
- When the shells are at a large distance apart, the potential energy approaches zero because the interaction between the charges diminishes.
- The final potential energy Ufinal=0.
- According to the law of conservation of energy:
Initial Kinetic Energy+Initial Potential Energy=Final Kinetic Energy+Final Potential Energy
- Initially, the kinetic energy is zero (the shells are at rest), so we have:
0+Uinitial=Kfinal+0
- Therefore, the final kinetic energy of the system (K) is equal to the initial potential energy:
K=Uinitial=kQ2d+kQ2R
- Since the kinetic energy is shared equally between the two shells, the kinetic energy of each shell Keach is:
Keach=K2=12(kQ2d+kQ2R)
The kinetic energy of each sphere when they are at a large distance apart is:
Keach=12(kQ2d+kQ2R)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (G)
7 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (H)
5 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (E)
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
A spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
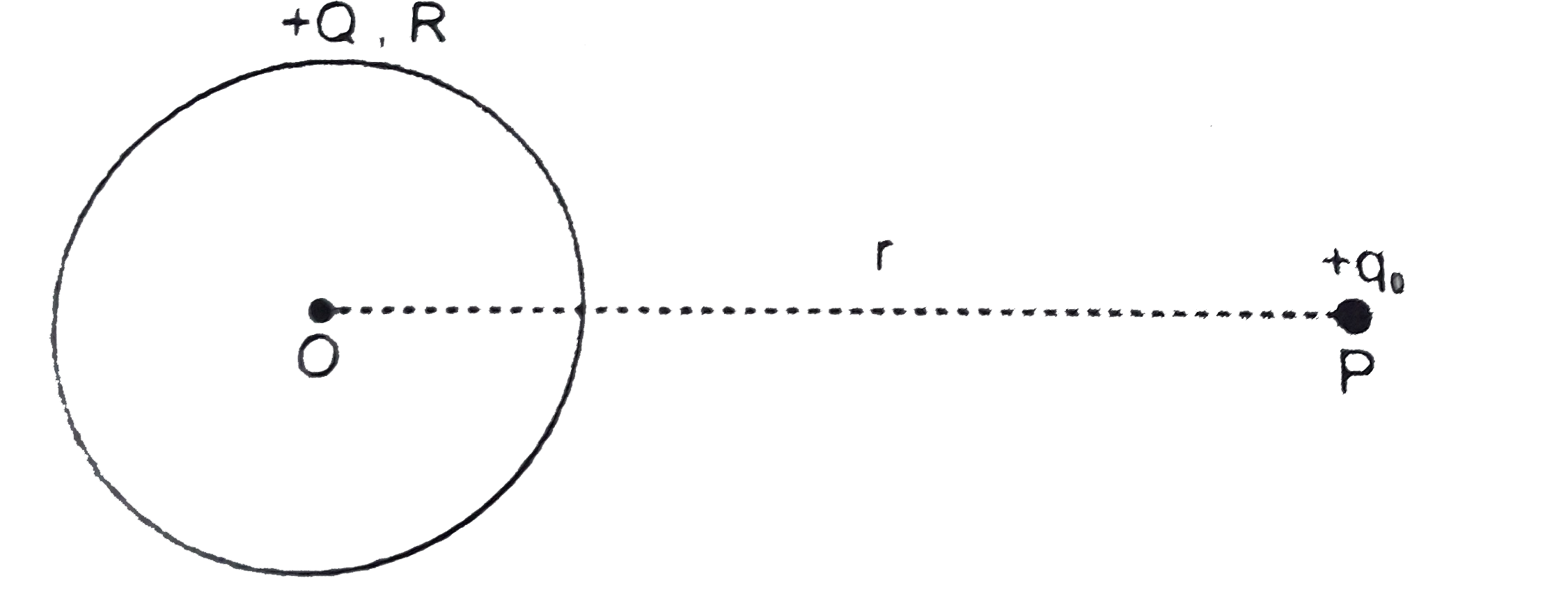
View SolutionA thin non-conducting hemispherical shell contains a positive charge q on it, which uniformly distributed on the shell. A point P lies on the diameter of shell as show in figure. Then the direction of electric field at the point 'P' is

View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
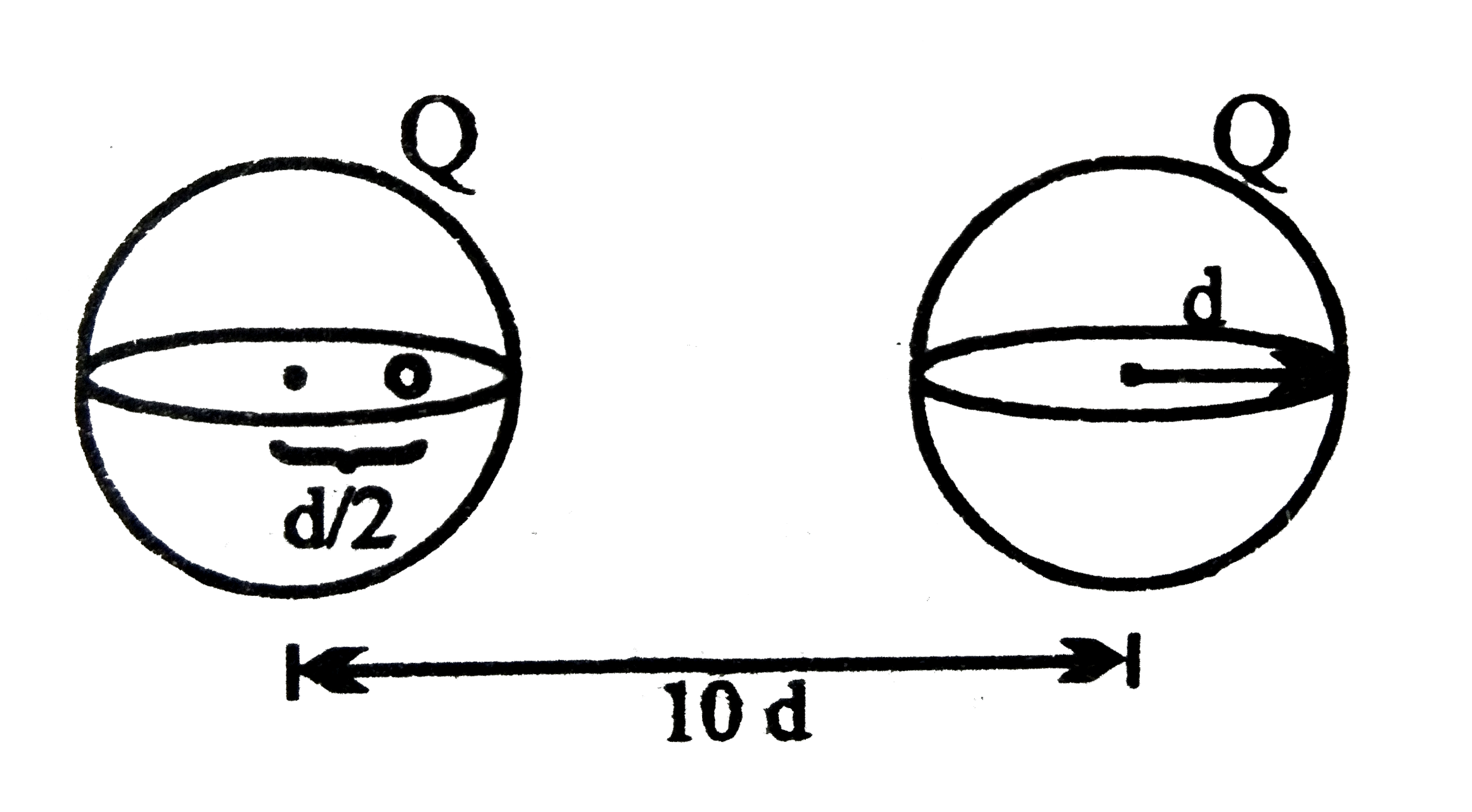
View SolutionTwo spherical , nonconducting and very tin shells of uniformly distributed positive charge Q and radius d are located a distance 10d from each other . A positive point charge q is placed inside one of the shells at a distance d/2 from the center, on the line connecting the centers of the two shells , as shown in the figure, What is the net force on the charge q ? .
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
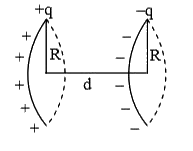
View SolutionTwo identical conducting sphere carrying different charges attact each other with a force F when placed in air medium at a distance d apart. The spheres are brought into contact and then taken to their original positions. Now, the two sphere repel each other with a force whole magnitude is equal to the initial attractive force. The ratio between initial charges on the spheres is
View SolutionA uniformly charged non-conducting spherical shell is given +q charge and a point charge -q is placed as shown. The electric field lines will be

View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

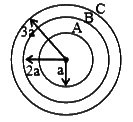
View SolutionThree concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -
View Solution
