Two uniform solid spheres of same materical and same radius are touching each other density is then find out gravitational force between them .
The correct Answer is:
To find the gravitational force between two uniform solid spheres of the same material and radius that are touching each other, we can follow these steps:
Step 1: Understand the Setup
We have two uniform solid spheres, each with radius r and density ρ. They are touching each other.
Step 2: Determine the Mass of Each Sphere
The mass m of each sphere can be calculated using the formula for mass:
m=density×volume
The volume V of a sphere is given by:
V=43πr3
Thus, the mass of each sphere is:
m=ρ×43πr3
Step 3: Calculate the Distance Between the Centers
Since the spheres are touching each other, the distance d between their centers is:
d=2r
Step 4: Apply Newton's Law of Gravitation
According to Newton's law of gravitation, the gravitational force F between two masses m1 and m2 separated by a distance d is given by:
F=Gm1m2d2
In our case, both spheres have the same mass m, so we can write:
F=Gm⋅m(2r)2
Step 5: Substitute the Mass and Distance
Substituting the mass m and the distance d:
F=G(ρ43πr3)(ρ43πr3)(2r)2
This simplifies to:
F=G(ρ2(43πr3)2)4r2
Step 6: Simplify the Expression
Now, we simplify the expression:
F=Gρ2(169π2r6)4r2
F=G16ρ2π2r636r2
F=49Gπ2ρ2r4
Final Answer
Thus, the gravitational force F between the two spheres is given by:
F=49Gπ2ρ2r4
We have two uniform solid spheres, each with radius r and density ρ. They are touching each other.
The mass m of each sphere can be calculated using the formula for mass:
m=density×volume
The volume V of a sphere is given by:
V=43πr3
Thus, the mass of each sphere is:
m=ρ×43πr3
Since the spheres are touching each other, the distance d between their centers is:
d=2r
According to Newton's law of gravitation, the gravitational force F between two masses m1 and m2 separated by a distance d is given by:
F=Gm1m2d2
In our case, both spheres have the same mass m, so we can write:
F=Gm⋅m(2r)2
Substituting the mass m and the distance d:
F=G(ρ43πr3)(ρ43πr3)(2r)2
This simplifies to:
F=G(ρ2(43πr3)2)4r2
Now, we simplify the expression:
F=Gρ2(169π2r6)4r2
F=G16ρ2π2r636r2
F=49Gπ2ρ2r4
Thus, the gravitational force F between the two spheres is given by:
F=49Gπ2ρ2r4
Topper's Solved these Questions
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:EXERCISE-1 PART-2
Explore 21 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:EXERCISE-1 PART-3
Explore 2 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:EXAMPLE
Explore 2 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Advance level Problems
Explore 35 Videos
- NUCLEAR PHYSICSBook:RESONANCE ENGLISHChapter:NUCLEAR PHYSICSExercise:Advanced level solutions
Explore 16 Videos
Similar Questions
Spheres of the same material and same radius r are touching each other. Show that gravitational force between them is directly proportional to r4.
View SolutionSpheres of the same material and same radius r are touching each other. Show that gravitational force between them is directly proportional to r4.
View Solution
Knowledge Check
If the distance between two point particles is doubled, then the gravitational force between them
Adecreases by a factor of 4Bdecreases by a factor of 2Cincreases by a factor of 2Dincreases by a factor of 4
Two spheres of the same material and same radius r are touching each other. If the gravitational force of attraction between them is directly proportional to rn, then the value of n is :
View Solution_S01_005_Q01.png)
Two solid sphere of same size of a metal are placed in contact by touching each other prove that the gravitational force acting between then is directly proportional to the fourth power of their radius.
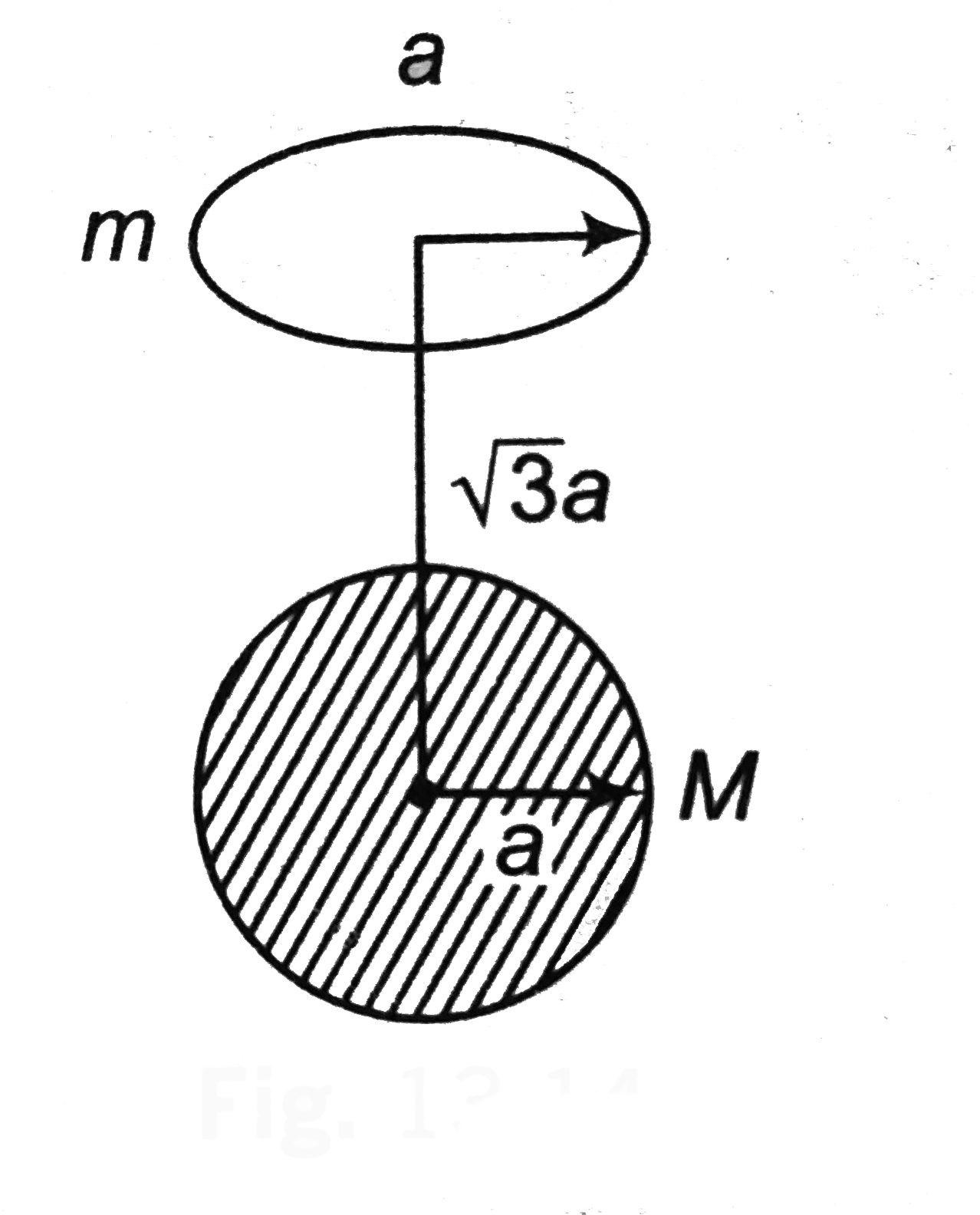
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View SolutionFour equal circles, each of radius 5cm, touch each other as shown in Figure. Find the area included between them.
View SolutionFour equal circles, each of radius 5 cm, touch each other as shown in Fig.20. Find the area included between them. (Takeπ=3.14).
View SolutionA particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View Solution