If f(x)=log10xandg(x)=elnxandh(x)=f[g(x)], then find the value of h(10).
The correct Answer is:1
To solve the problem step by step, we will follow the definitions of the functions given and calculate h(10).
Step 1: Define the functions
We have the following functions defined:
- f(x)=log10x
- g(x)=elnx
- h(x)=f(g(x))
Step 2: Simplify g(x)
We know from properties of logarithms and exponentials that:
g(x)=elnx=x
This is because the exponential function e and the natural logarithm ln are inverse functions.
Step 3: Substitute g(x) into h(x)
Now we substitute g(x) into h(x):
h(x)=f(g(x))=f(x)
This means that h(x) is simply f(x).
Step 4: Calculate h(10)
Now we need to find h(10):
h(10)=f(10)
Substituting into the function f:
f(10)=log10(10)
Step 5: Evaluate log10(10)
We know that:
log10(10)=1
Final Answer
Thus, the value of h(10) is:
h(10)=1
We have the following functions defined:
- f(x)=log10x
- g(x)=elnx
- h(x)=f(g(x))
We know from properties of logarithms and exponentials that:
g(x)=elnx=x
This is because the exponential function e and the natural logarithm ln are inverse functions.
Now we substitute g(x) into h(x):
h(x)=f(g(x))=f(x)
This means that h(x) is simply f(x).
Now we need to find h(10):
h(10)=f(10)
Substituting into the function f:
f(10)=log10(10)
We know that:
log10(10)=1
Thus, the value of h(10) is:
h(10)=1
Topper's Solved these Questions
- MATRICES & DETERMINANTBOOK - RESONANCE ENGLISHCHAPTER - MATRICES & DETERMINANTEXERCISE - PART-II:
28 Videos
- INDEFINITE INTEGRATION BOOK - RESONANCE ENGLISHCHAPTER - INDEFINITE INTEGRATION EXERCISE - SELF PRACTIC PROBLEMS
25 Videos
- NUMBER THEORYBOOK - RESONANCE ENGLISHCHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)
4 Videos
Similar Questions
Knowledge Check
If f(x) = x log x and g(x) = 10x , then g(f(2)) =
A24B17C4D2
If f(x)=logexandg(x)=ex, then prove that :
f(g(x)}=g{f(x)}
View SolutionIf f(x)=|log10x| then at x=1.
View SolutionIf f, g, h are real functions defined by f=√x+1, g(x)=1x and h(x)=2x2−3, then find the values of (2fg+g−h)(1) and (2f+g−h)(1).
View SolutionSuppose f and g are two functions such that f,g: R →R f(x)=ln(1+√1+x2) and g(x)=ln(x+√1+x2) then find the value of xeg(x)f(1x)+g'(x) at x=1
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
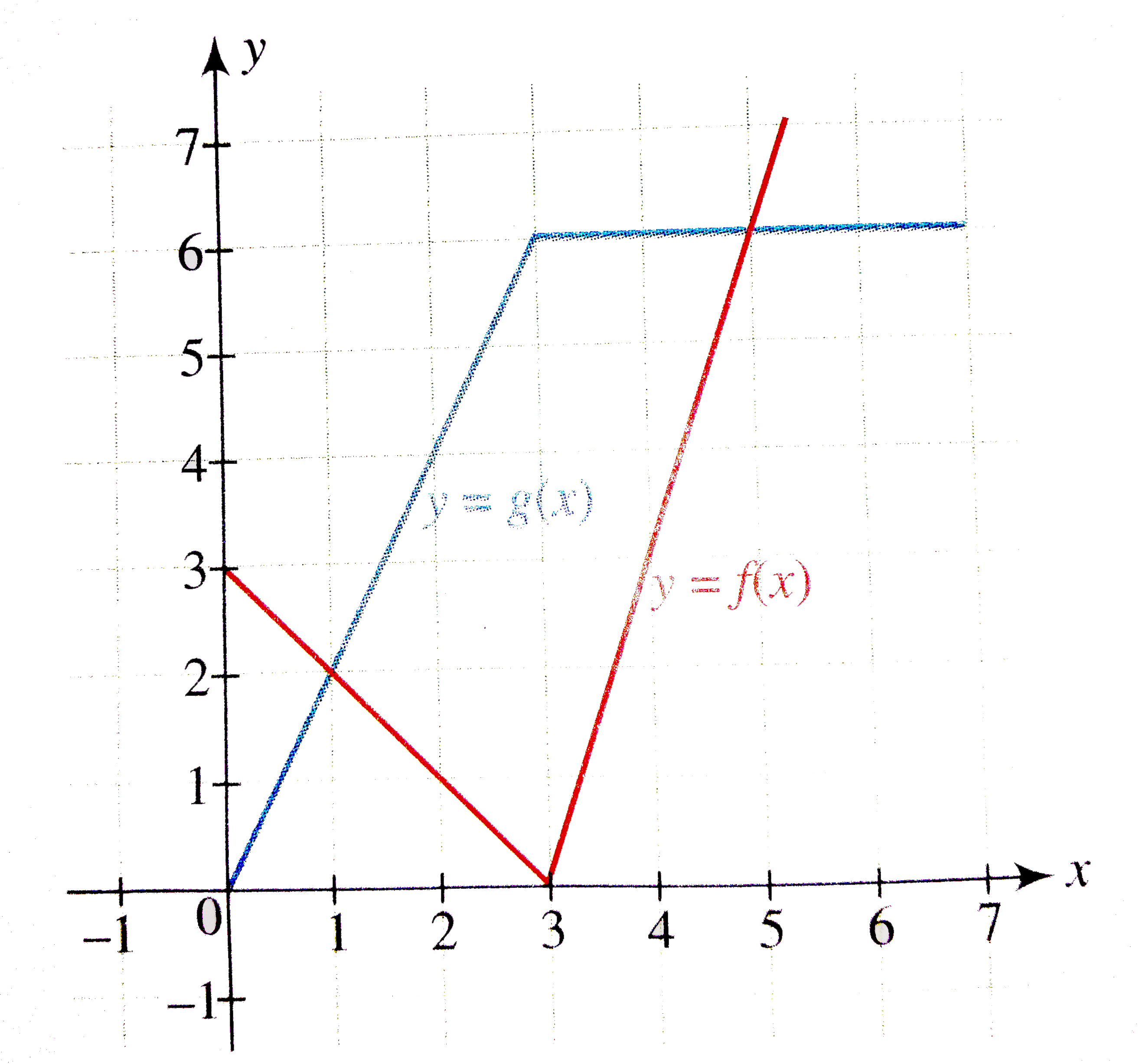
View SolutionIf f(x)=logx(logx), then find f'(x)atx=e
View SolutionTwo functions f(x)andg(x) are defined as f(x)=(log)3∣∣∣x−2x2−10x+24∣∣∣ and g(x)=cos−1(x−23), then find the number of even integers for which (f(x)+g(x)) is defined.
View Solution
