Question

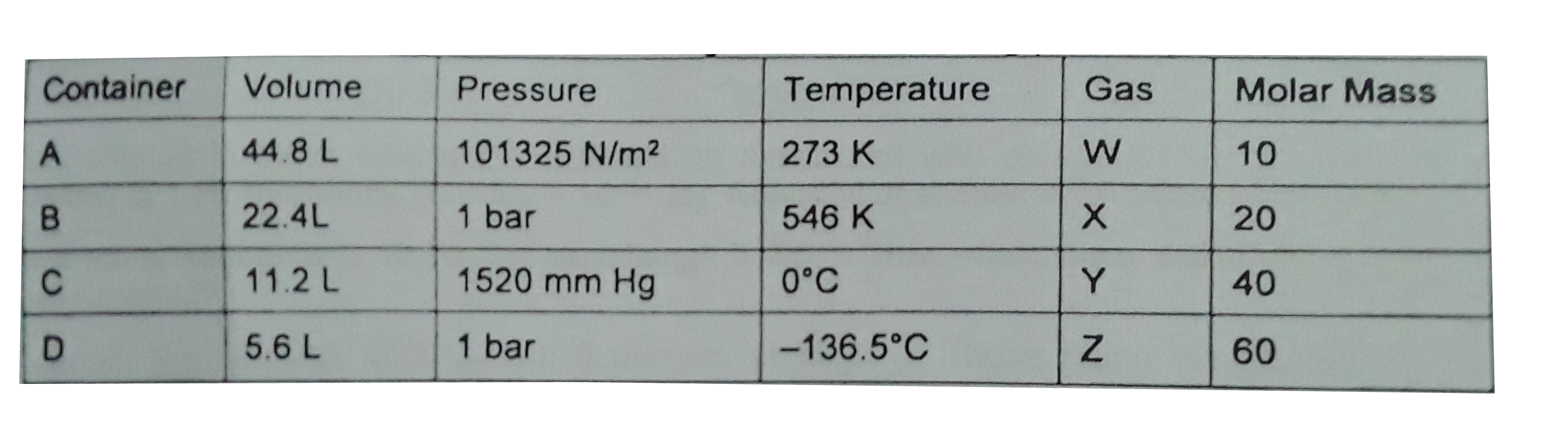
Three different containers contain three different gases with following parameter
Container 1 of 67.2 L containing gas X at $0^{\circ }C$ and 1.01325 bar
Container 2 of 44. 8L contaning gas Y at 546 K & 760 mm of Hg
Container 3 of 89.6 L containing Z gas at 101325 $N/m^2\&0^{\circ }C$
Now they are mixed in single container. If gram molecular mass of X ,Y & Z are 10 g/mol, 20 g/mol and 40 g/mol respectively Then which of the following statements are correct

Options

A. Mole percent of gas Z in final mixture is 50%
B. Average molecular mass of final mixture is 26.25 amu
C. Mole ratio of gas X and gas Z is 3:4
D. Number of molecules present in final mixture is equal to number of atoms in 320 g Ca

Explanation

To solve the problem, we will follow these steps:

Step 1: Calculate the number of moles of each gas using the Ideal Gas Law.

The Ideal Gas Law is given by the equation:
\( PV = nRT \)
Where:
- \( P \) = pressure (in atm)
- \( V \) = volume (in liters)
- \( n \) = number of moles
- \( R \) = universal gas constant = 0.0821 L·atm/(K·mol)
- \( T \) = temperature (in Kelvin)

For Gas X:
- Volume (\( V \)) = 67.2 L
- Pressure (\( P \)) = 1.01325 bar = 1 atm (since 1 bar ≈ 1 atm)
- Temperature (\( T \)) = 0°C = 273 K

Using the formula:
\( n_X = \frac{PV}{RT} = \frac{(1 \, \text{atm})(67.2 \, \text{L})}{(0.0821 \, \text{L·atm/(K·mol)})(273 \, \text{K})} \)
Calculating this gives:
\( n_X = \frac{67.2}{22.414} \approx 3 \, \text{moles} \)

For Gas Y:
- Volume (\( V \)) = 44.8 L
- Pressure (\( P \)) = 760 mmHg = 1 atm
- Temperature (\( T \)) = 546 K

Using the formula:
\( n_Y = \frac{PV}{RT} = \frac{(1 \, \text{atm})(44.8 \, \text{L})}{(0.0821 \, \text{L·atm/(K·mol)})(546 \, \text{K})} \)
Calculating this gives:
\( n_Y \approx 1 \, \text{mole} \)

For Gas Z:
- Volume (\( V \)) = 89.6 L
- Pressure (\( P \)) = 101325 N/m² = 1 atm
- Temperature (\( T \)) = 0°C = 273 K

Using the formula:
\( n_Z = \frac{PV}{RT} = \frac{(1 \, \text{atm})(89.6 \, \text{L})}{(0.0821 \, \text{L·atm/(K·mol)})(273 \, \text{K})} \)
Calculating this gives:
\( n_Z = \frac{89.6}{22.414} \approx 4 \, \text{moles} \)

Step 2: Calculate the total number of moles.
\( n_{total} = n_X + n_Y + n_Z = 3 + 1 + 4 = 8 \, \text{moles} \)

Step 3: Calculate the mole percentages of each gas.
- Mole percentage of gas X:
\( \text{Mole percent of X} = \left(\frac{n_X}{n_{total}}\right) \times 100 = \left(\frac{3}{8}\right) \times 100 = 37.5\% \)

- Mole percentage of gas Y:
\( \text{Mole percent of Y} = \left(\frac{n_Y}{n_{total}}\right) \times 100 = \left(\frac{1}{8}\right) \times 100 = 12.5\% \)

- Mole percentage of gas Z:
\( \text{Mole percent of Z} = \left(\frac{n_Z}{n_{total}}\right) \times 100 = \left(\frac{4}{8}\right) \times 100 = 50\% \)

Step 4: Calculate the average molecular mass of the mixture.
Using the formula:
\( \text{Average molecular mass} = \frac{(n_X \cdot M_X) + (n_Y \cdot M_Y) + (n_Z \cdot M_Z)}{n_{total}} \)
Where:
- \( M_X = 10 \, \text{g/mol} \)
- \( M_Y = 20 \, \text{g/mol} \)
- \( M_Z = 40 \, \text{g/mol} \)

Calculating:
\( \text{Average molecular mass} = \frac{(3 \cdot 10) + (1 \cdot 20) + (4 \cdot 40)}{8} = \frac{30 + 20 + 160}{8} = \frac{210}{8} = 26.25 \, \text{g/mol} \)

Step 5: Determine the mole ratio of gas X to gas Z.
\( \text{Mole ratio of X to Z} = \frac{n_X}{n_Z} = \frac{3}{4} \, \text{or} \, 3:4 \)

Step 6: Calculate the number of molecules in the final mixture.
Using Avogadro's number (\( 6.022 \times 10^{23} \)):
\( \text{Total number of molecules} = n_{total} \times N_A = 8 \times 6.022 \times 10^{23} \)

Step 7: Calculate the number of moles of calcium in 320 g.
\( \text{Moles of Ca} = \frac{320 \, \text{g}}{40 \, \text{g/mol}} = 8 \, \text{moles} \)
Thus, the number of atoms in 320 g of calcium is also \( 8 \times 6.022 \times 10^{23} \).

Conclusion:
All statements provided in the question are true:
1. Mole percent of Z is 50%.
2. Average molecular mass is 26.25 g/mol.
3. Mole ratio of X to Z is 3:4.
4. Number of molecules in the final mixture equals the number of atoms in 320 g of calcium.