Niels Bohr a Danish physicist received his PhD from the University of Copenhagen in 1911. He that spent a year with J.J. Thomson and Ernest Rutherford in England. In 1913, he returned to Copenhagen Where he remained for the rest of his life. In 1920 he was named Director of the Institute of theory! Physics After first World War Bohr worked energetically for peaceful uses of atomic energy recieved the first Atoms for Peace award in 1957 Bohr was awarded the Nobel Prize in Physics
1922
(a) The Angular momentum of an electron in a given stationary state can be expressed as mevr=h2π
where n=1, 2,3 ...... Thus an electron can move only in those orbits for which its angular momentum is integral multiple of h/2π that is why only certain fixed orbits are alowed
(b) The radii of the stationary states are expressed as rn=n2a0 where a0=52.9 pm. Thus the radius the first stationary state, called the Bohr radius, is 52.9 pm. Normally the electron in the hydrogen atom is found in this orbit (that is n =1). As n increases the value of r will increase
(c) The most important property associated with the electronEn=−2.18×10−18(Z2n2)J n=1,2,3
(d)it is also possible to calculate to calculate the velocities of electrons moving in these orbits by using vn=2.18106×Znm/sec. Qualitatively the magnitude of velocity of electron increases with increase of positive charge on the nucleus and decreases with increases the value of n.
(e)Bohr's theory can also be applied to th ions containing only one electron, similar to that present it hydrogen atom. For example , He+Li2+,Be3+ and so on.
given by the expression Ex=-218x n=1,2,3 (d) It is also possible to calculate the velocities of electrons moving in these orbits by using V 2.1810 cm/sec Qualitatively the magnitude of velocity of electron increases with increase of positive charge on the nucleus and decreases with increase the value of n (e) Bohr's theory can also be applied to the ions containing only one electron, similar to that presenti hydrogen atom For example, Help, Be and so on
Choose the incorrect curve :
if v=velocity of electron in Bohr's orbit
r=Radius of electron in Bohr's orbit
P.E.=Potential energy of electron in Bohr's orbit
K.E.=Kinetic energy of the electron in Bohr's orbit.
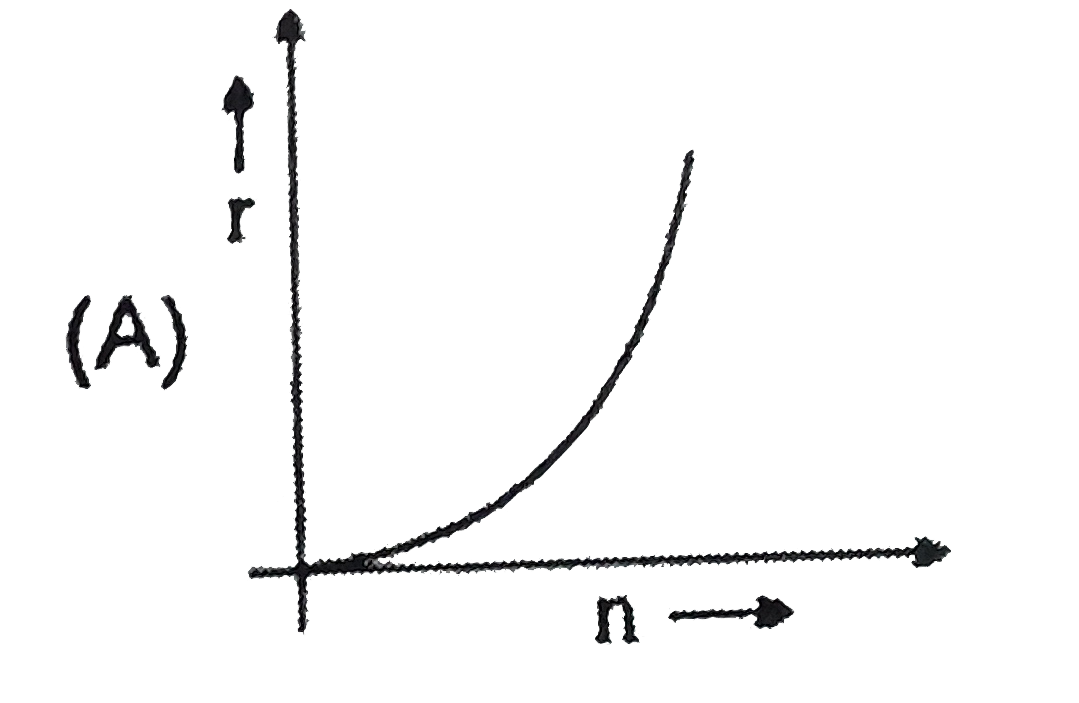
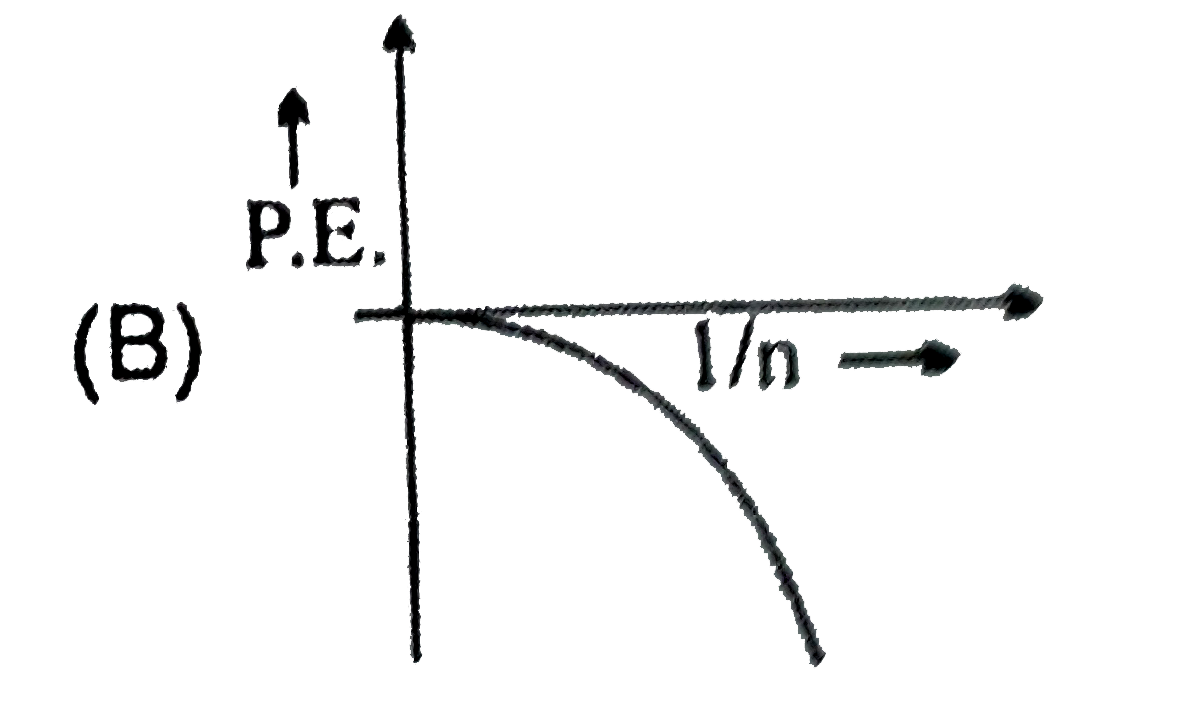
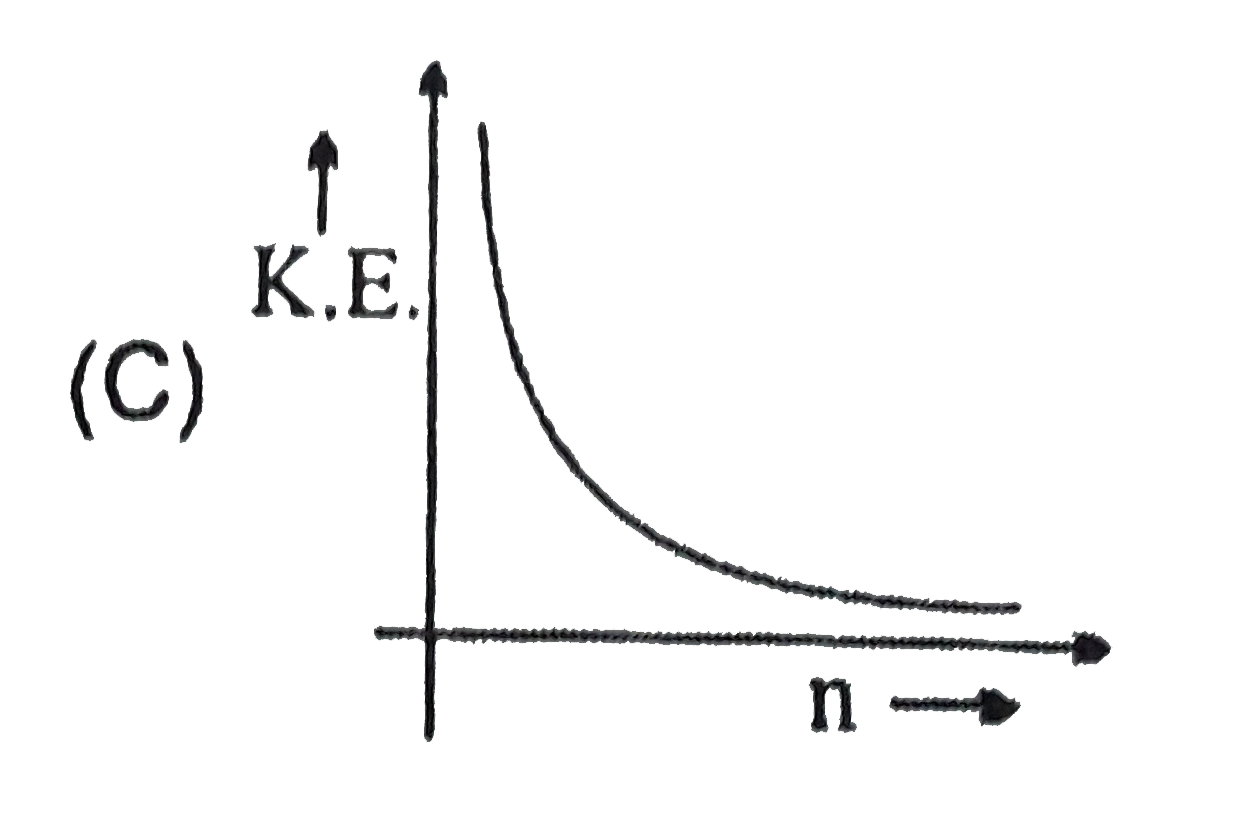
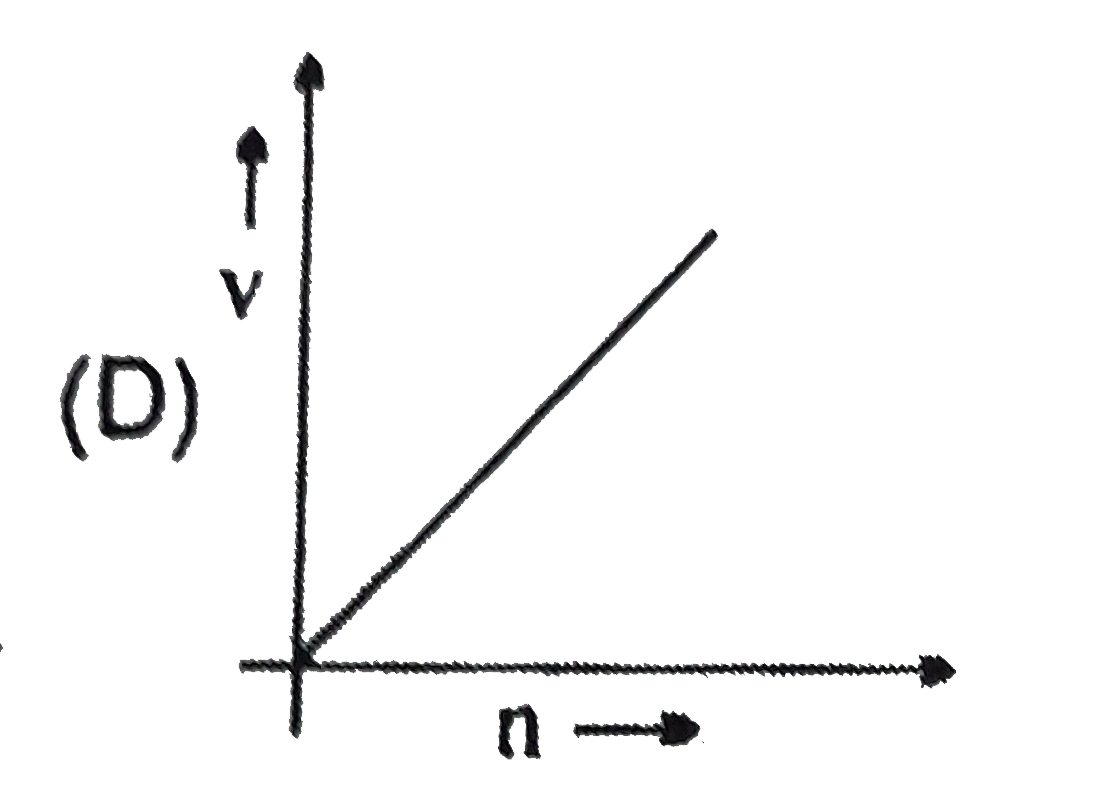
To solve the question regarding the incorrect curve related to the properties of an electron in Bohr's orbit, we need to analyze the relationships between the velocity (v), radius (r), potential energy (P.E.), and kinetic energy (K.E.) of the electron in the context of Bohr's model.
1. Understanding the Relationships:
- According to Bohr's model, the kinetic energy (K.E.) of an electron in orbit is given by:
K.E.=12mev2
- The potential energy (P.E.) of the electron due to the electrostatic force between the electron and the nucleus is given by:
P.E.=−k⋅e2r
- The total energy (E) of the electron is the sum of its kinetic and potential energy:
E=K.E.+P.E.
2. Kinetic Energy and Potential Energy Relation:
- From Bohr's theory, it is known that:
K.E.=−12P.E.
- This means that the kinetic energy is always half the magnitude of the potential energy but with a positive sign.
3. Velocity and Radius Relationship:
- The velocity of the electron can be expressed as:
v=Z⋅e22⋅ϵ0⋅h
- The radius of the electron's orbit is given by:
rn=n2a0
- As the principal quantum number (n) increases, the radius increases, but the velocity decreases.
4. Analyzing the Curves:
- The curves typically represent the relationships between K.E., P.E., and the radius or velocity of the electron.
- The K.E. curve should be a function of the radius (or n) and should show that as the radius increases, K.E. decreases.
- The P.E. curve should show that as the radius increases, P.E. becomes less negative (increases).
5. Identifying the Incorrect Curve:
- If any curve suggests that K.E. increases with increasing radius or that P.E. becomes more negative with increasing radius, that would be incorrect.
- The correct relationships are that K.E. decreases and P.E. becomes less negative as the radius increases.
Conclusion:
The incorrect curve would be one that contradicts the established relationships between kinetic energy, potential energy, and radius in Bohr's model.
- According to Bohr's model, the kinetic energy (K.E.) of an electron in orbit is given by:
K.E.=12mev2
- The potential energy (P.E.) of the electron due to the electrostatic force between the electron and the nucleus is given by:
P.E.=−k⋅e2r
- The total energy (E) of the electron is the sum of its kinetic and potential energy:
E=K.E.+P.E.
- From Bohr's theory, it is known that:
K.E.=−12P.E.
- This means that the kinetic energy is always half the magnitude of the potential energy but with a positive sign.
- The velocity of the electron can be expressed as:
v=Z⋅e22⋅ϵ0⋅h
- The radius of the electron's orbit is given by:
rn=n2a0
- As the principal quantum number (n) increases, the radius increases, but the velocity decreases.
- The curves typically represent the relationships between K.E., P.E., and the radius or velocity of the electron.
- The K.E. curve should be a function of the radius (or n) and should show that as the radius increases, K.E. decreases.
- The P.E. curve should show that as the radius increases, P.E. becomes less negative (increases).
- If any curve suggests that K.E. increases with increasing radius or that P.E. becomes more negative with increasing radius, that would be incorrect.
- The correct relationships are that K.E. decreases and P.E. becomes less negative as the radius increases.
The incorrect curve would be one that contradicts the established relationships between kinetic energy, potential energy, and radius in Bohr's model.
Topper's Solved these Questions
Similar Questions
Of the ions Ag+,Co2+ and Ti4+ ,which ones will be coloured in aqueous solutions. (Atomic numbers:)
Ag = 47 , Co = 27, Ti = 22)
(b) If each one of the above ionic species is in turn placed in magnetic field, how will it respond and why?
View SolutionA very thin copper plate is electro− plated with gold using gold chloride in HCl. The current was passed for 20min. And the increase in the weight of the plate was found to be 2g.[Au=197]. The current passed was −
View SolutionThe energy of the second Bohr orbit in the hydrogen atom is −3.41eV. The energy of the second Bohr orbit of He+ ion would be :
View SolutionCalculate the energy of an electron in the first Bohr orbit ofHe+.
View SolutionWhat does he get from Anil in return for his work?
View SolutionThe energy of an electron in the first Bohr orbit for He^(+) ion is -54.4eV. Which one of the following is a possible excited state for electron in Bohr orbit of He^(+) ion?
View SolutionThe energy of the second Bohr orbit of the hydrogen atom is -3.41 eV . The energy of the second Bohr orbit of the He^+ ion will be _______.
View SolutionThe energy of the second Bohr orbit of H atom is -3.41 eV. The energy of the second Bohr orbit of He^(+) ion is
View SolutionWhat does he get from Anil in return for his work?
View SolutionThe energy of the second Bohr orbit in the hydrogen atom is −3.41eV. The energy of the second Bohr orbit of He+ ion would be :
View Solutionकथनः He परमाणु के लिए बोहर मॉडल मान्य नहीं होता है।
कारणः बोहर सिद्धांत के अंतर्गत अंतर इलेक्ट्रॉनिक प्रतिकर्षण की व्याख्या नहीं की गई।
View Solutionडेनिस भौतिकविद निल्स बोहर ने 1911 में यूनिवर्सिटी ऑफ कोपहेगन से Ph.D की थी। इसके पश्चात उन्होंने एक वर्ष जे जे थॉमस तथा अरनेस्ट रदाफोर्ड के साथ इलैण्ड में गुजारा था। 1913 में, उन्हें इंस्टिट्यूट ऑफ फिजिक्स के डाइरेक्टर की उपाधि से नवाजा गया। प्रथम विश्व युद्ध के पश्चात बोहर ने परमाणु ऊर्जा के शान्तिपूर्ण उपयोग के लिए प्रभावशाली ढंग से काम किया। उन्होंने 1957 में शान्ति पुरस्कार प्राप्त किया। बोहर को 1922 में भौतिक में नोबल पुरस्कार दिया गया।
(a) दी गई स्थायी कक्षा में इलेक्ट्रॉन को कोणीय संवेग mevr=n.h2π द्वारा व्यक्त किया जाता है, जहाँ n=1,2,3…. अतः इलेक्ट्रॉन केवल उन कक्षाओं में चक्कर लगाता है जिनमे इसका कोणीय संवेग h/2π का पूर्ण गुणज होता है। अतः केवल कुछ निश्चित कक्षा ही सम्भव है।
(b) स्थायी अवस्था में त्रिज्या rn=n2a0 द्वारा व्यक्त कि जाती है। जहाँ a0=52.9 pm है। अतः प्रथम स्थायी अवस्था कि त्रिज्या, जिसे बोहर त्रिज्या कहा जाता है, 52.9 pm होती है। सामान्यतः हाइड्रोजन परमाणु में इलेक्ट्रॉन इस कक्षक (n=1) में पाया जाता है। n का मान बढ़ने पर बढ़ता है।
(c ) इलेक्ट्रॉन से संबंधित महत्वपूर्ण गन, इसके स्थायी कक्षा की ऊर्जा है। यह निम्न व्यंजक दवरा दी जाती है -
En=−2.18×10−18(Z2n2)Jn=1,2,3....
(d) इन कक्षको में चक्कर लगाने वाले इलेक्ट्रॉन के वेग की गणना vn=2.18×106×Znm/sec से प्रयुक्त की जाती है। इलेक्ट्रॉन के वेग का गुणात्मक मान नाभिक पर धनावेश बढ़ने पर बढ़ता है तथा का मान बढ़ने पर घटता है। बोहर सिद्धान्त एकल इलेक्ट्रॉन वाले आयनों, जो हाइड्रोजन परमाणु के समान है पर भी लागू होता है। उदाहरण के लिए He+Li2+,Be3 इत्यादि।
गलत वक्र चुनिए :
यदि v = बोहर कक्षा में इलेक्ट्रॉन का वेग।
r = बोहर कक्षा में इलेक्ट्रॉन की त्रिज्या।
P.E. = बोहर कक्षा में इलेक्ट्रॉन की स्थितिज ऊर्जा।
K.E. = बोहर कक्षा में इलेक्ट्रॉन की गतिज ऊर्जा।
View SolutionThe energy of the second Bohr orbit of the hydrogen atom is -3.41 eV. The energy of the third Bohr orbit of the He ion will be
View SolutionThe energy of the second Bohr orbit in the hydrogen atom is −3.41eV. The energy of the second Bohr orbit of He+ ion would be :
View SolutionCalculate the energy of an electron in the first Bohr orbit of He^(+) .
View Solution
