Which is the correct relationship mentioned in bracket :
CH3−CNandCH3NC (Functional isomers)
CH3−O−N=OandCH3−N∣∣O→O (Functional isomers)
CH3−CH2−CH2−CHOandH3C−C∣CHOH−CH3 (Chain isomers)
H−C∣∣O−C∣∣O−O−C∣CH3H−CH3and H−C∣∣O−O−C∣∣O−CH2−CH2−CH3 (Functional isomers)
To solve the question regarding the correct relationship mentioned in the bracket, we need to analyze the concepts of isomerism in organic chemistry, specifically focusing on functional isomers and chain isomers.
1. Understanding Isomerism:
- Isomerism refers to the phenomenon where compounds have the same molecular formula but different structural formulas. This leads to different physical and chemical properties.
2. Identifying Functional Isomers:
- Functional isomers are compounds that have the same molecular formula but different functional groups. For example, C2H6O can represent both ethanol (an alcohol) and dimethyl ether (an ether).
- In the context of the question, we need to identify if the compounds mentioned have different functional groups.
3. Identifying Chain Isomers:
- Chain isomers are compounds that have the same molecular formula but differ in the arrangement of the carbon skeleton. This can include straight-chain and branched-chain forms.
- For example, C4H10 can be butane (straight-chain) or isobutane (branched).
4. Identifying Position Isomers:
- Position isomers have the same functional group but differ in the position of that functional group on the carbon chain.
- For example, C3H7Br can represent 1-bromopropane and 2-bromopropane.
5. Analyzing the Given Compounds:
- From the video transcript, we can see that the compounds mentioned have different functional groups (e.g., -OH, -CHO, -NO2).
- Therefore, they can be classified as functional isomers.
6. Conclusion:
- The correct relationship mentioned in the bracket is that the compounds are functional isomers since they have the same molecular formula but different functional groups.
Final Answer:
The correct relationship is that the compounds are functional isomers.
- Isomerism refers to the phenomenon where compounds have the same molecular formula but different structural formulas. This leads to different physical and chemical properties.
- Functional isomers are compounds that have the same molecular formula but different functional groups. For example, C2H6O can represent both ethanol (an alcohol) and dimethyl ether (an ether).
- In the context of the question, we need to identify if the compounds mentioned have different functional groups.
- Chain isomers are compounds that have the same molecular formula but differ in the arrangement of the carbon skeleton. This can include straight-chain and branched-chain forms.
- For example, C4H10 can be butane (straight-chain) or isobutane (branched).
- Position isomers have the same functional group but differ in the position of that functional group on the carbon chain.
- For example, C3H7Br can represent 1-bromopropane and 2-bromopropane.
- From the video transcript, we can see that the compounds mentioned have different functional groups (e.g., -OH, -CHO, -NO2).
- Therefore, they can be classified as functional isomers.
- The correct relationship mentioned in the bracket is that the compounds are functional isomers since they have the same molecular formula but different functional groups.
The correct relationship is that the compounds are functional isomers.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which is the correct relationship between ΔG∘ and equilibrium constant Kp?
Aa. Kp=−RTlogΔG∘Bb. Kp=[E/RT]ΔG∘Cc. Kp=−ΔG∘/RTDd. Kp=e−ΔG∘/RT
Which is the correct property mentioned −
View SolutionIdentify the correct relationship:
View SolutionWhich of these is the correct relationship between bar and atmosphere?
View SolutionWhich of these is the correct relationship between liter and mm3?
View SolutionWhich is not correct relationship between ΔGΘ and equilibrium constant KP.
View SolutionIf Eɵcell for a given reaction is negative, which gives the correct relationships for the values of ΔGɵ and Keq?
View SolutionMention the correct relationship between I and II :
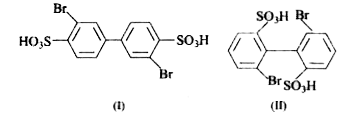
View Solution
