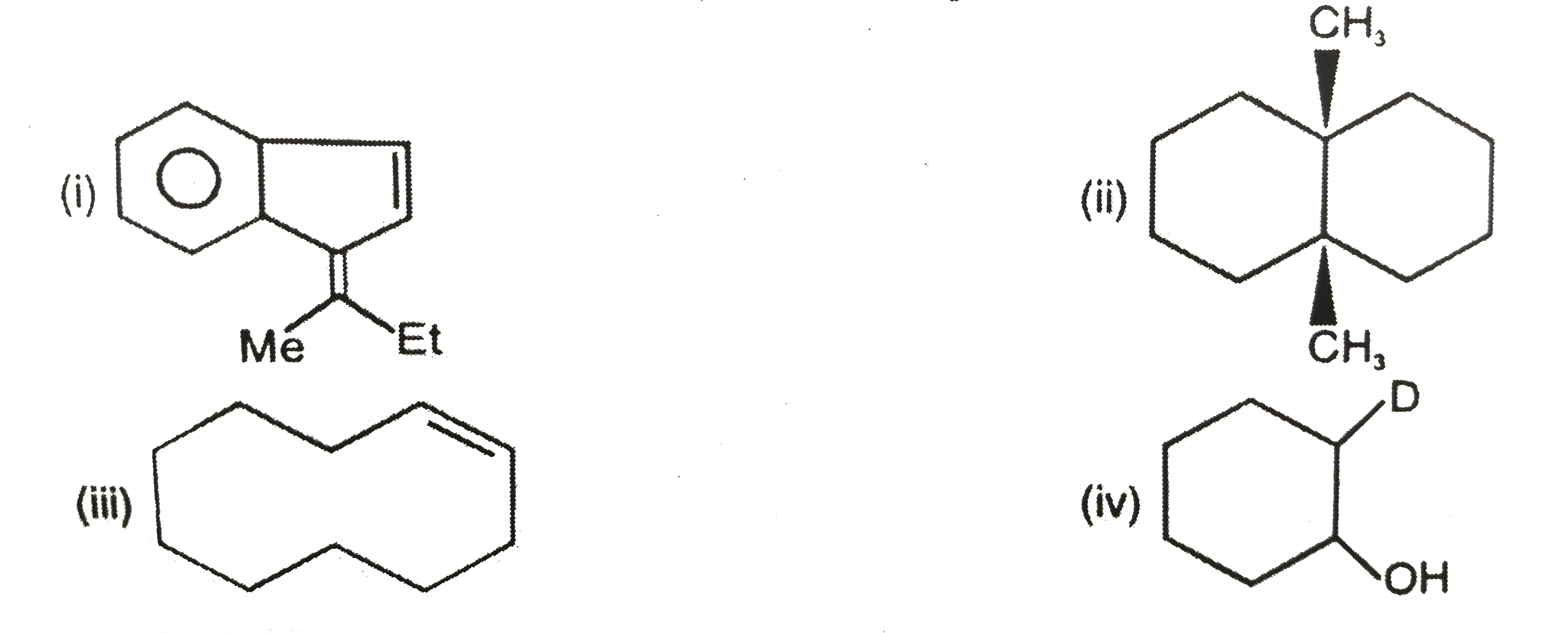
Define restricted rotation and give on example each of acyclic and cyclic compound, which can show geometrical isomersm.
The correct Answer is:The bond across which atoms cannot rotate without breaking the bonds is called restricted rotation. e.g.
C=C, C=N, ring etc (##RESCHMSIME01003_A01##) (a ≠ b, d ≠ e)
Step-by-Step Text Solution:
Step 1: Define Restricted Rotation
Restricted rotation refers to the limitation of the free rotation around a bond, typically due to the presence of a double bond or a cyclic structure. This restriction occurs because of the high energy barrier that prevents the rotation from occurring freely between different conformations.
Step 2: Example of a Cyclic Compound Showing Geometrical Isomerism
An example of a cyclic compound that exhibits geometrical isomerism is 1,2-dibromocyclopentane. In this compound, the two bromine atoms can be positioned either on the same side of the ring (cis isomer) or on opposite sides (trans isomer).
- Cis Isomer: Both bromine atoms are on the same side of the cyclopentane ring.
- Trans Isomer: The bromine atoms are on opposite sides of the cyclopentane ring.
The restricted rotation around the carbon-carbon bonds in the ring prevents the easy interconversion between these two isomers.
Step 3: Example of an Acyclic Compound Showing Geometrical Isomerism
An example of an acyclic compound that can show geometrical isomerism is 2-butene. In 2-butene, the two methyl groups can either be on the same side (cis isomer) or on opposite sides (trans isomer) of the double bond.
- Cis Isomer: The two methyl groups are on the same side of the double bond.
- Trans Isomer: The two methyl groups are on opposite sides of the double bond.
The presence of the double bond creates a restriction to rotation, resulting in distinct geometrical isomers.
Restricted rotation refers to the limitation of the free rotation around a bond, typically due to the presence of a double bond or a cyclic structure. This restriction occurs because of the high energy barrier that prevents the rotation from occurring freely between different conformations.
An example of a cyclic compound that exhibits geometrical isomerism is 1,2-dibromocyclopentane. In this compound, the two bromine atoms can be positioned either on the same side of the ring (cis isomer) or on opposite sides (trans isomer).
- Trans Isomer: The bromine atoms are on opposite sides of the cyclopentane ring.
An example of an acyclic compound that can show geometrical isomerism is 2-butene. In 2-butene, the two methyl groups can either be on the same side (cis isomer) or on opposite sides (trans isomer) of the double bond.
- Trans Isomer: The two methyl groups are on opposite sides of the double bond.
Topper's Solved these Questions
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART 1 SECTION (B))
2 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART 1 SECTION (C))
2 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART III : PRACTICE TEST-2 (IIT-JEE (ADVANCED PATTERN))
23 Videos
- SOLUTIONSBOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - Advabced Level Problems (PART-2)
35 Videos
- STRUCTURAL IDENTIFICATIONBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATIONEXERCISE - Advanced level Problems (Part-III)
12 Videos
Similar Questions
Knowledge Check
Which of the following compound can show geometrical isomerism ?
A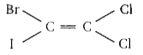 B
B C
C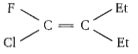 D
D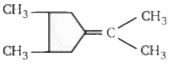
Identify number of compounds that can show geometrical isomerism.
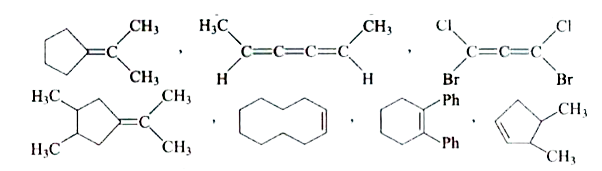
View SolutionWhich of the following can show geometrical isomerism.
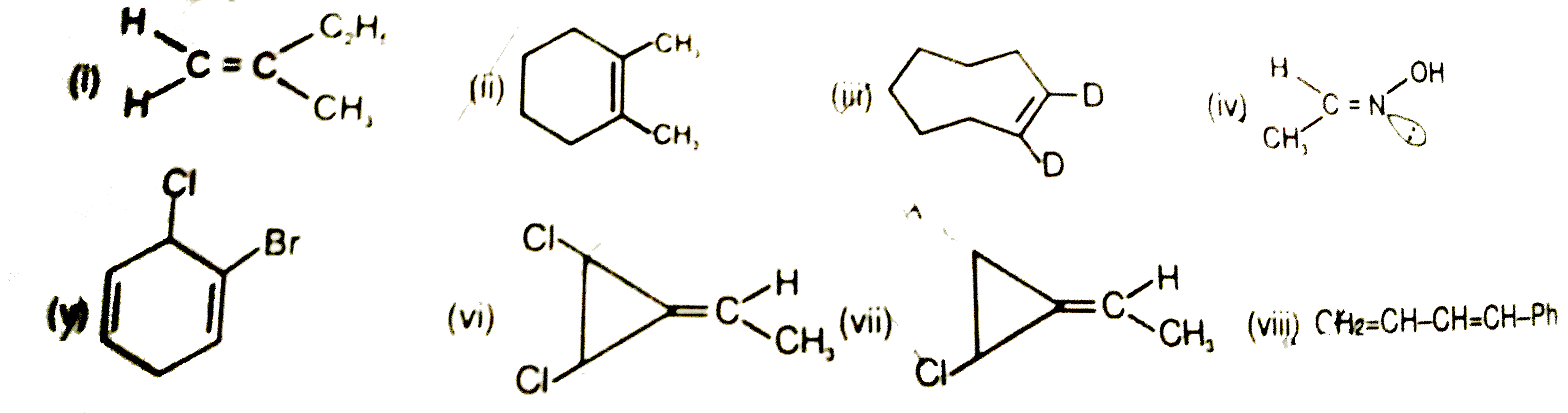
View SolutionWhich among the following compounds will show geometrical isomerism.
View SolutionWhich of the following compound will show geometrical isomerism?
View SolutionWhich of the following can show geometrical isomerism?
View SolutionWhich of the following compound can not show geometrical isomerism?1
View SolutionWhich of the following compounds will not show geometrical isomerism?
View Solution