The minimum torsional strain developed in butane is at dihedral angle (s)
0^(º), 108^(º)
120∘,240º
60∘,180∘,300∘
60∘,120∘,180∘
The correct Answer is:C
To determine the minimum torsional strain developed in butane, we need to analyze the molecular structure and the concept of dihedral angles. Here’s a step-by-step solution:
Step 1: Understand Butane Structure
Butane (C₄H₁₀) consists of four carbon atoms connected in a straight chain. The structural formula can be represented as:
CH3−CH2−CH2−CH3
Step 2: Define Torsional Strain
Torsional strain arises from the repulsion between electrons in bonds that are eclipsed or close to each other. In butane, the torsional strain is influenced by the arrangement of hydrogen and methyl (CH₃) groups around the carbon-carbon bonds.
Step 3: Dihedral Angles and Staggered vs. Eclipsed Conformations
- Dihedral Angle: The angle between the planes formed by two sets of atoms in a molecule. In butane, we can consider the dihedral angle between the hydrogen atoms or between a hydrogen and a methyl group on adjacent carbons.
- Staggered Conformation: When the groups on adjacent carbons are positioned as far apart as possible (e.g., 60° or 180°).
- Eclipsed Conformation: When the groups are aligned with each other (e.g., 0° or 120°).
Step 4: Analyze Conformations
1. Staggered Conformation:
- At a dihedral angle of 60°, the groups are staggered, resulting in lower torsional strain.
- At a dihedral angle of 180°, the groups are in an anti-conformation, which also results in minimal repulsion and thus low torsional strain.
- At a dihedral angle of 300°, the groups are again staggered, leading to low torsional strain.
2. Eclipsed Conformation:
- At 0° and 120°, the groups are eclipsed, leading to higher torsional strain due to increased electron repulsion.
Step 5: Conclusion
The minimum torsional strain in butane occurs at staggered conformations, specifically at dihedral angles of 60°, 180°, and 300°. Among these, the most stable conformation is at 180°, where the methyl groups are opposite each other.
Final Answer
The minimum torsional strain developed in butane is at dihedral angles of 60°, 180°, and 300°.
---
Butane (C₄H₁₀) consists of four carbon atoms connected in a straight chain. The structural formula can be represented as:
CH3−CH2−CH2−CH3
Torsional strain arises from the repulsion between electrons in bonds that are eclipsed or close to each other. In butane, the torsional strain is influenced by the arrangement of hydrogen and methyl (CH₃) groups around the carbon-carbon bonds.
- Dihedral Angle: The angle between the planes formed by two sets of atoms in a molecule. In butane, we can consider the dihedral angle between the hydrogen atoms or between a hydrogen and a methyl group on adjacent carbons.
- Staggered Conformation: When the groups on adjacent carbons are positioned as far apart as possible (e.g., 60° or 180°).
- Eclipsed Conformation: When the groups are aligned with each other (e.g., 0° or 120°).
1. Staggered Conformation:
- At a dihedral angle of 60°, the groups are staggered, resulting in lower torsional strain.
- At a dihedral angle of 180°, the groups are in an anti-conformation, which also results in minimal repulsion and thus low torsional strain.
- At a dihedral angle of 300°, the groups are again staggered, leading to low torsional strain.
- At 0° and 120°, the groups are eclipsed, leading to higher torsional strain due to increased electron repulsion.
The minimum torsional strain in butane occurs at staggered conformations, specifically at dihedral angles of 60°, 180°, and 300°. Among these, the most stable conformation is at 180°, where the methyl groups are opposite each other.
The minimum torsional strain developed in butane is at dihedral angles of 60°, 180°, and 300°.
Topper's Solved these Questions
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART II SECTION (K))
6 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART III MATCH THE COLUMN)
1 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART II SECTION (I))
9 Videos
- SOLUTIONSBOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - Advabced Level Problems (PART-2)
35 Videos
- STRUCTURAL IDENTIFICATIONBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATIONEXERCISE - Advanced level Problems (Part-III)
12 Videos
Similar Questions
An aluminium wire is clamped at each end and under zero stress at room temperature. Temperature of room decreases resulting into development of thermal stress & thermal strain in the wire. Cross-sectional area of the wire is 5.00×10−6m2. Density of aluminium is 2.70×103kg/m3. Young’s modulus of aluminium is 7.00×1010N/m2. A transverse wave speed of 100 m/s generates in the wire due to a resulting thermal strain (Δll) developed in the wire. The thermal strain (Δll) is: (l is original length of the wire)
View Solution(a) Draw sawhorse projection formulae for the two eclipsed conformations of butane.
(b) What is the dihedral angle between adjaccent methyl groups? (c) Which conformer has greater torsional strain?
View Solution
Knowledge Check
Assertion: Staggered conformation of ethane is most stable while eclipsed conformation is least stable. ltbr> Reason: Staggered form has the least torsional strain and the eclipsed form has the maximum torsional strain.
AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
In figure the upper wire is made of steel and the lower of copper. The wires have equal cross section. Find the ratio of the longitudinal strains developed in the two wires.

View SolutionThere is no ring strain in cyclohexane, but cyclobutane has an angle strain of 9∘ 44'. If ΔH∘c of cyclohexane per (CH2) group is 660 kJ mol−1 and ΔH∘c of cyclobutane is 2744 kJ mol−1, what is the ring strain in kJ mol−1 of cyclobutane ?
View SolutionFor a prism of refractive index 1.732, the angle of minimum deviation is equal to the angle of the prism. The angle of the prism is
View SolutionA light ray of angles of incidence 40∘ emerged from the prism in minimum deviation position. Then what is the angle of incidence on the second surface ?
View SolutionWhat should be the minimum value of refractive index of a prism, refracting angle A, so that there is no emergent ray irrespective of the angle of incidence?

View SolutionTorsion strain is the repulsive interaction between
View SolutionIn the following skew conformatioin of ethane, H'−C−C−H'' dihedral angle is :
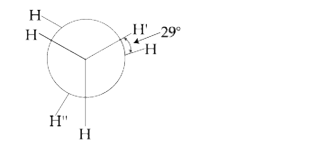
View Solution
