A compound is chiral even if
a mirror plane is present
a centre of inversion exists
a rotation axis axists
an improper rotation axis is present
The correct Answer is:C
To determine the conditions under which a compound is chiral, we need to understand the concept of chirality and the characteristics of chiral molecules. Here’s a step-by-step breakdown of the solution:
Step 1: Define Chirality
A compound is considered chiral if it is not superimposable on its mirror image. This means that the compound and its mirror image cannot be aligned perfectly, similar to how left and right hands are distinct.
Hint: Remember that chirality is often compared to the concept of handedness.
Step 2: Identify Characteristics of Chiral Compounds
Chiral compounds typically possess one or more stereocenters (usually carbon atoms bonded to four different groups) and lack certain symmetry elements that would allow for superimposition.
Hint: Look for the presence of stereocenters and the absence of symmetry elements.
Step 3: Analyze the Given Statements
The question provides four statements regarding the conditions under which a compound is chiral:
1. A mirror plane is present.
2. A center of inversion exists.
3. A rotation axis exists.
4. An improper rotation axis is present.
Hint: Consider how each of these symmetry elements affects chirality.
Step 4: Evaluate Each Statement
- Statement 1: A mirror plane is present. (Incorrect) - The presence of a mirror plane indicates symmetry, which typically means the compound is achiral.
- Statement 2: A center of inversion exists. (Incorrect) - A center of inversion also indicates symmetry and thus would render the compound achiral.
- Statement 3: A rotation axis exists. (Correct) - The presence of a proper rotation axis (C_n where n > 1) can indicate chirality if there are no other symmetry elements present.
- Statement 4: An improper rotation axis is present. (Incorrect) - The presence of an improper rotation axis suggests symmetry, leading to achirality.
Step 5: Conclusion
Based on the analysis, the correct answer is that a compound can be chiral if a rotation axis exists, provided there are no other symmetry elements (like a mirror plane or center of inversion) that would make it achiral.
Final Answer: A compound is chiral even if a rotation axis exists.
Hint: Focus on the relationship between symmetry elements and chirality when evaluating compounds.
A compound is considered chiral if it is not superimposable on its mirror image. This means that the compound and its mirror image cannot be aligned perfectly, similar to how left and right hands are distinct.
Chiral compounds typically possess one or more stereocenters (usually carbon atoms bonded to four different groups) and lack certain symmetry elements that would allow for superimposition.
The question provides four statements regarding the conditions under which a compound is chiral:
1. A mirror plane is present.
2. A center of inversion exists.
3. A rotation axis exists.
4. An improper rotation axis is present.
- Statement 1: A mirror plane is present. (Incorrect) - The presence of a mirror plane indicates symmetry, which typically means the compound is achiral.
- Statement 2: A center of inversion exists. (Incorrect) - A center of inversion also indicates symmetry and thus would render the compound achiral.
- Statement 3: A rotation axis exists. (Correct) - The presence of a proper rotation axis (C_n where n > 1) can indicate chirality if there are no other symmetry elements present.
- Statement 4: An improper rotation axis is present. (Incorrect) - The presence of an improper rotation axis suggests symmetry, leading to achirality.
Based on the analysis, the correct answer is that a compound can be chiral if a rotation axis exists, provided there are no other symmetry elements (like a mirror plane or center of inversion) that would make it achiral.
Topper's Solved these Questions
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART III : PRACTICE TEST-2 (IIT-JEE (ADVANCED PATTERN))
23 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (ADDITIONAL PROBLEMS FOR SELF PRACTICE (APSP)) PART 1
30 Videos
- SOLUTIONSBOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - Advabced Level Problems (PART-2)
35 Videos
- STRUCTURAL IDENTIFICATIONBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATIONEXERCISE - Advanced level Problems (Part-III)
12 Videos
Similar Questions
Knowledge Check
Which of the following compounds is chiral?
A B
B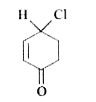 C
C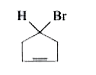 D
D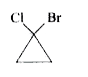
Which of the following compounds is chiral?
A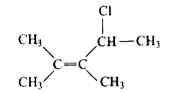 B
B C
C DAll of these
DAll of theseThe compound that is chiral is
A3-methyl-3-hexeneB4chloro-1-methycyclohexaneC2-phenylpentaneD1,3-disopropylbenzene
The compound that is chiral
View SolutionWhich of the following compounds is not chiral?
View SolutionWhich of the following compounds is not chiral?
View SolutionThe formation of an optically active compound from a chiral molecule is called:
View SolutionWhich of the following compounds possesses chiral carbon?
View Solution
