A={1,2,3,...,9}. If three numbers are selected from set A and are arranged, the probability that three numbers are either in increasing order or in decreasing order.
16
23
12
13
The correct Answer is:D
To solve the problem, we need to find the probability that three numbers selected from the set A={1,2,3,…,9} are arranged in either increasing or decreasing order.
1. Determine the Total Ways to Select and Arrange 3 Numbers:
- First, we need to select 3 numbers from the set of 9. The number of ways to choose 3 numbers from 9 is given by the combination formula:
(nr)=n!r!(n−r)!
Here, n=9 and r=3:
(93)=9!3!(9−3)!=9×8×73×2×1=84
2. Calculate the Arrangements of the Selected Numbers:
- Once we have selected 3 numbers, we can arrange them in 3! (factorial of 3) ways:
3!=6
- Therefore, the total number of arrangements of any 3 selected numbers is:
Total arrangements=(93)×3!=84×6=504
3. Determine the Favorable Outcomes (Increasing or Decreasing Order):
- For any set of 3 distinct numbers, there are exactly 2 arrangements that are either in increasing order or in decreasing order. For example, if we select the numbers 1, 2, and 3, they can be arranged as:
- Increasing: 1,2,3
- Decreasing: 3,2,1
- Hence, the total number of favorable outcomes is:
Favorable outcomes=(93)×2=84×2=168
4. Calculate the Probability:
- The probability P that the three selected numbers are either in increasing or decreasing order is given by the ratio of the number of favorable outcomes to the total arrangements:
P=Favorable outcomesTotal arrangements=168504
- Simplifying this fraction:
P=168÷168504÷168=13
Final Answer:
The probability that three numbers selected from set A are either in increasing order or in decreasing order is 13.
- First, we need to select 3 numbers from the set of 9. The number of ways to choose 3 numbers from 9 is given by the combination formula:
(nr)=n!r!(n−r)!
Here, n=9 and r=3:
(93)=9!3!(9−3)!=9×8×73×2×1=84
- Once we have selected 3 numbers, we can arrange them in 3! (factorial of 3) ways:
3!=6
- Therefore, the total number of arrangements of any 3 selected numbers is:
Total arrangements=(93)×3!=84×6=504
- For any set of 3 distinct numbers, there are exactly 2 arrangements that are either in increasing order or in decreasing order. For example, if we select the numbers 1, 2, and 3, they can be arranged as:
- Increasing: 1,2,3
- Decreasing: 3,2,1
- Hence, the total number of favorable outcomes is:
Favorable outcomes=(93)×2=84×2=168
- The probability P that the three selected numbers are either in increasing or decreasing order is given by the ratio of the number of favorable outcomes to the total arrangements:
P=Favorable outcomesTotal arrangements=168504
- Simplifying this fraction:
P=168÷168504÷168=13
The probability that three numbers selected from set A are either in increasing order or in decreasing order is 13.
Topper's Solved these Questions
- TEST PAPERBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - CHEMISTRY
24 Videos
- SEQUENCE & SERIES BOOK - RESONANCE ENGLISHCHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)
3 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
259 Videos
Similar Questions
Knowledge Check
Three numbers are chosen at random from 1 to 20 .The probability that they are consecutive is
A1190B1120C3190D5190Arrange the following in decreasing order of E2 reaction :
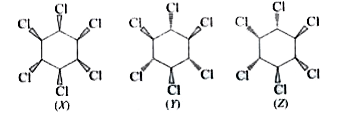 AX>Y>ZBX>Z>YCZ>X>YDY>X>Z
AX>Y>ZBX>Z>YCZ>X>YDY>X>ZArrange the following in decreasing order of E2 reaction :
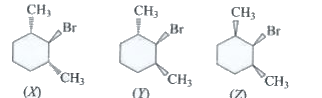 AX>Y>ZBX>Z>YCY>Z>XDZ>Y>X
AX>Y>ZBX>Z>YCY>Z>XDZ>Y>X
Three numbers are chosen at random from numbers 1 to 30. Write the probability that the chosen number are consecutive.
View SolutionThree distinct number are selected from first 100 natural numbers. The probability that all the numbers are divisible by 2 and 3 is _________
View SolutionThree numbers are chosen from 1 to 30. The probability that they are not consecutive is
View SolutionThree dice are thrown together. The probability that the sum of the numbers appearing on them is 9, is
View SolutionThree-digit numbers are formed using the digits 0,1,2,3,4,5 without repetition of digits. If a number is chosen at random, then the probability that the digits either increase or decrease, is
View Solution
