For how many integers n is √9−(n+2)2 a real number?
The correct Answer is:7
To determine for how many integers n the expression √9−(n+2)2 is a real number, we need to ensure that the quantity under the square root is non-negative. This leads us to the following steps:
Step 1: Set up the inequality
We start with the condition for the square root to be real:
9−(n+2)2≥0
Step 2: Rearrange the inequality
Rearranging gives us:
(n+2)2≤9
Step 3: Take the square root
Taking the square root of both sides (and remembering to consider both the positive and negative roots), we have:
−n−2≤3andn+2≤3
−n−2≥−3andn+2≥−3
Step 4: Solve the inequalities
Now we solve these inequalities one by one.
1. From (n+2)2≤9:
- n+2≤3 leads to:
n≤1
- n+2≥−3 leads to:
n≥−5
Step 5: Combine the results
Combining these results, we find:
−5≤n≤1
Step 6: Identify integer solutions
Now we need to find the integer values of n within this range:
- The integers that satisfy −5≤n≤1 are:
−5,−4,−3,−2,−1,0,1
Step 7: Count the integers
Counting these integers gives us a total of:
7 integers
Conclusion
Thus, the total number of integers n for which √9−(n+2)2 is a real number is 7.
---
We start with the condition for the square root to be real:
9−(n+2)2≥0
Rearranging gives us:
(n+2)2≤9
Taking the square root of both sides (and remembering to consider both the positive and negative roots), we have:
−n−2≤3andn+2≤3
−n−2≥−3andn+2≥−3
Now we solve these inequalities one by one.
- n+2≤3 leads to:
n≤1
- n+2≥−3 leads to:
n≥−5
Combining these results, we find:
−5≤n≤1
Now we need to find the integer values of n within this range:
- The integers that satisfy −5≤n≤1 are:
−5,−4,−3,−2,−1,0,1
Counting these integers gives us a total of:
7 integers
Thus, the total number of integers n for which √9−(n+2)2 is a real number is 7.
Topper's Solved these Questions
- NUMBER THEORYBOOK - RESONANCE ENGLISHCHAPTER - NUMBER THEORYEXERCISE - Exercise -1 (PART - II)
5 Videos
- NUMBER THEORYBOOK - RESONANCE ENGLISHCHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - I)
22 Videos
- NUMBER THEORYBOOK - RESONANCE ENGLISHCHAPTER - NUMBER THEORYEXERCISE - Self Practice Problems
4 Videos
- MATRICES & DETERMINANTBOOK - RESONANCE ENGLISHCHAPTER - MATRICES & DETERMINANTEXERCISE - HLP
34 Videos
- RELATION, FUNCTION & ITFBOOK - RESONANCE ENGLISHCHAPTER - RELATION, FUNCTION & ITFEXERCISE - SSP
55 Videos
Similar Questions
Knowledge Check
For how many integers n is (7n−26)(5n+11) a negative number ?
ANoneBTwoCFourDSixFor how many positive integers n is it true that the sum of 13/n, 18/n and 29/n is an integer?
A6B60CGreatest common factor of 13,18 and 29D12For how many integers n between 5 and 20, inclusive, is the sum of 3n, 9n and 11n greater than 200?
A4B8C12D16
Consider the following statements :
1. N∪(B∩Z)=(N∪B)∩Z for any subset B of R, where N is the set of positive integers, Z is the set of integers, R is the set of real numbers.
2. Let A={n∈N:1≥n≥24,nis a multiple of3}. There exists no subsets B of N such that the number of elements in A is equal to the number of elements in B.
Which of the above statemetns is/are correct ? (A) 1 only (B) 2 only (C) Both 1 and 2 (D) Neither 1 nor 2
View SolutionLet [x] denote the greatest integer part of a real number x, if M=40∑n=1[n22] then M equals
View SolutionFind the smallest positive integer value of n for which (1+i)n(1−i)n−2 is a real number.
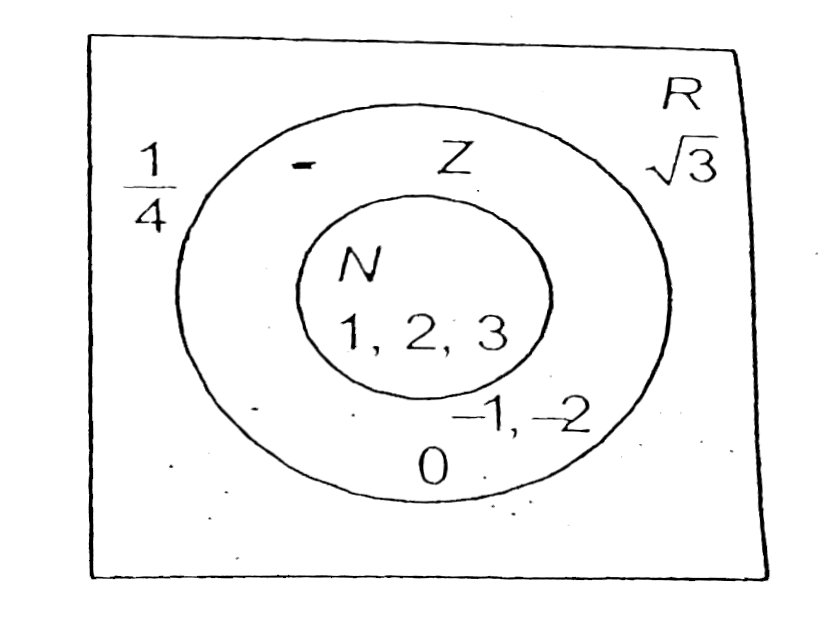
View SolutionNatural number are subsets of integers are subsets of real number i.e. N⊂Z,Z⊂R,N⊂R
View Solution|n−1|<4
How many integer n satisfy the inequality above?
View Solution
