In how many ways can the 7 letters A, B, C, D, E, F, and G be arranged so that C and E are never together?
The correct Answer is:3600
To find the number of ways to arrange the letters A, B, C, D, E, F, and G such that C and E are never together, we can follow these steps:
Step 1: Calculate the total arrangements of the 7 letters
The total number of ways to arrange 7 distinct letters is given by the factorial of the number of letters.
Total arrangements=7!=7×6×5×4×3×2×1=5040
Step 2: Calculate the arrangements where C and E are together
To find the arrangements where C and E are together, we can treat C and E as a single unit or block. Therefore, we will have the following blocks to arrange: (CE), A, B, D, F, G. This gives us a total of 6 blocks to arrange.
Arrangements with C and E together=6!=6×5×4×3×2×1=720
Step 3: Account for the arrangements of C and E within their block
Since C and E can be arranged within their block in 2 different ways (CE or EC), we need to multiply the arrangements of the blocks by 2.
Total arrangements with C and E together=6!×2=720×2=1440
Step 4: Calculate the arrangements where C and E are never together
To find the arrangements where C and E are never together, we subtract the arrangements where C and E are together from the total arrangements.
Arrangements where C and E are never together=7!−(Arrangements with C and E together)
=5040−1440=3600
Final Answer
Thus, the number of ways to arrange the letters A, B, C, D, E, F, and G such that C and E are never together is 3600.
---
The total number of ways to arrange 7 distinct letters is given by the factorial of the number of letters.
To find the arrangements where C and E are together, we can treat C and E as a single unit or block. Therefore, we will have the following blocks to arrange: (CE), A, B, D, F, G. This gives us a total of 6 blocks to arrange.
Since C and E can be arranged within their block in 2 different ways (CE or EC), we need to multiply the arrangements of the blocks by 2.
To find the arrangements where C and E are never together, we subtract the arrangements where C and E are together from the total arrangements.
Thus, the number of ways to arrange the letters A, B, C, D, E, F, and G such that C and E are never together is 3600.
Topper's Solved these Questions
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-1 (Part-II RMO)
11 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-I: Previous Asked Question for Pre RMO)
17 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Self practice problems
30 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - High Level Problems (HLP)
35 Videos
- DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCE ENGLISHCHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - High Level Problem
26 Videos
Similar Questions
In how many ways can the letters of the word ARRANGE be arranged so that the two R's are never together.
View SolutionIn how many ways can the letters of the word 'ALGEBRA' be arranged, so that two A's are never together?
View Solution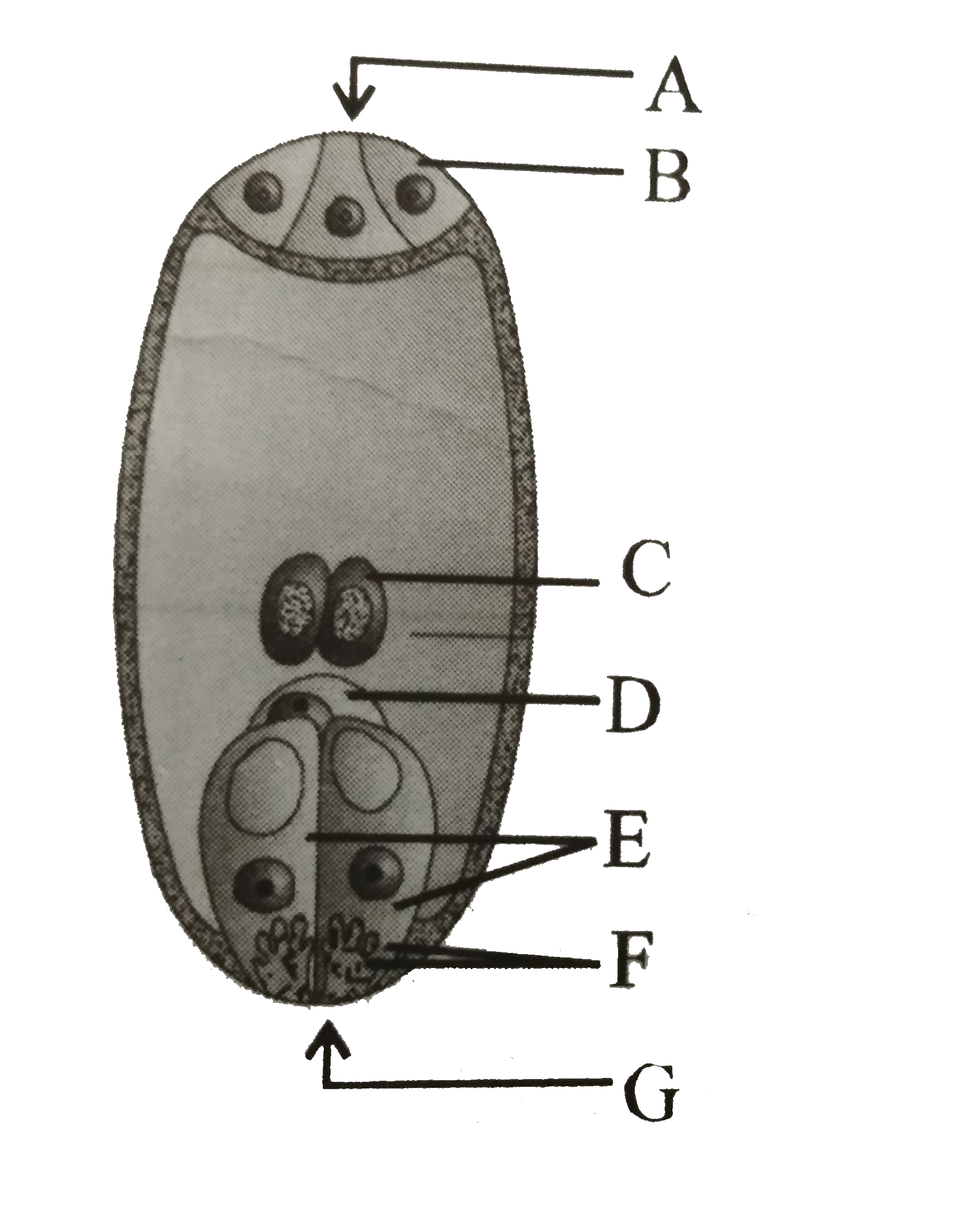
Identify A, B, C, D, E, F,G
View SolutionIn how many ways can the letters of the word BANARAS be arranged so that the letters N and S are never together
View SolutionIn how many ways can the letters of the word DIRECTOR be arranged so that the three vowels are never together?
View SolutionIn how many ways can the letters of the word ' COMBINE ' be arranged so that,
all the vowels never come together,
View SolutionIn how many ways can the letters of he word ARRANGE be arranged so that the two A\'s are together but not two R\'s
View SolutionIn how many ways can the letters of he word ARRANGE be arranged so that the two A's are together but not two R's
View SolutionIn how many ways can the letters of the word ' COMBINE ' be arranged so that, the vowels are never separated
View SolutionIn how many ways can the letters of the word ASSASSINATION be arranged so that all the S's are together ?
View Solution
