Consider the following sequence :a1=a2=1,ai=1+ minimum (ai−1,ai−2) for I>2. Then a2006=
The correct Answer is:1003
To solve the problem, we need to find the value of a2006 in the given sequence defined as follows:
1. a1=a2=1
2. For i>2, ai=1+min(ai−1,ai−2)
Let's calculate the terms step by step.
Step 1: Calculate the first few terms of the sequence
- For i=3:
a3=1+min(a2,a1)=1+min(1,1)=1+1=2
- For i=4:
a4=1+min(a3,a2)=1+min(2,1)=1+1=2
- For i=5:
a5=1+min(a4,a3)=1+min(2,2)=1+2=3
- For i=6:
a6=1+min(a5,a4)=1+min(3,2)=1+2=3
- For i=7:
a7=1+min(a6,a5)=1+min(3,3)=1+3=4
- For i=8:
a8=1+min(a7,a6)=1+min(4,3)=1+3=4
- For i=9:
a9=1+min(a8,a7)=1+min(4,4)=1+4=5
- For i=10:
a10=1+min(a9,a8)=1+min(5,4)=1+4=5
Step 2: Identify the pattern
From the calculations, we can observe the following pattern:
- The sequence appears to be:
1,1,2,2,3,3,4,4,5,5,…
This suggests that the even-indexed terms are equal to their half index, and the odd-indexed terms are the same as the previous even-indexed term.
Step 3: Generalize the formula
From the pattern, we can deduce:
- For even n (i.e., a2n), the term is n.
- For odd n (i.e., a2n−1), the term is also n.
Step 4: Calculate a2006
Since 2006 is even, we can use the formula:
a2006=a2×1003=1003
Final Answer
Thus, the value of a2006 is 1003.
2. For i>2, ai=1+min(ai−1,ai−2)
a3=1+min(a2,a1)=1+min(1,1)=1+1=2
a4=1+min(a3,a2)=1+min(2,1)=1+1=2
a5=1+min(a4,a3)=1+min(2,2)=1+2=3
a6=1+min(a5,a4)=1+min(3,2)=1+2=3
a7=1+min(a6,a5)=1+min(3,3)=1+3=4
a8=1+min(a7,a6)=1+min(4,3)=1+3=4
a9=1+min(a8,a7)=1+min(4,4)=1+4=5
a10=1+min(a9,a8)=1+min(5,4)=1+4=5
1,1,2,2,3,3,4,4,5,5,…
- For even n (i.e., a2n), the term is n.
- For odd n (i.e., a2n−1), the term is also n.
a2006=a2×1003=1003
Thus, the value of a2006 is 1003.
Topper's Solved these Questions
- SEQUENCE & SERIES Book:RESONANCE ENGLISHChapter:SEQUENCE & SERIES Exercise:EXERCISE -1 PART -II RMO
Explore 1 Video
- SEQUENCE & SERIES Book:RESONANCE ENGLISHChapter:SEQUENCE & SERIES Exercise:EXERCISE -2 (PART -I PREVIOUS ASKED QUESTION FOR PRE RMO)
Explore 15 Videos
- SEQUENCE & SERIES Book:RESONANCE ENGLISHChapter:SEQUENCE & SERIES Exercise:SELF PRACTICE PROBLEMS
Explore 23 Videos
- RELATION, FUNCTION & ITFBook:RESONANCE ENGLISHChapter:RELATION, FUNCTION & ITFExercise:SSP
Explore 55 Videos
- TEST PAPERBook:RESONANCE ENGLISHChapter:TEST PAPERExercise:MATHEMATICS
Explore 48 Videos
Similar Questions
In the following circuit i1 and i2 are respectively
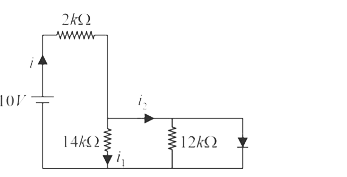
View SolutionIn the following circuit i1 and i2are respectively
View SolutionExpress the following in the form a+ib: (1+i1−i)2
View SolutionExpress the following in the form a+ib: (1+2i2+i)2
View SolutionExpress the following in the form of a+bi:(i) (−5i)(18i) (ii) (−i)(2i)(−18i)3
View SolutionConvert the following in the polar form :
(i) 1+7i(2−i)2
(ii) 1+3i1−2i
View SolutionSimplify the following: (−i)(2i)(−18i)3
View SolutionIf ai>0 for i=1,2,…., n and a1a2 … an=1 , then minimum value of (1+a1)(1+a2) ….. (1+an) is :
View SolutionIf ai>0 for iu=1,2,3,…,n and a1a2…an=1, then the minimum value of (1+a1)(1+a2)…(1+an), is
View SolutionExpress the following complex number in the polar form: (i) 1+7i(2−i)2 (ii) 1+3i1−2i
View Solution