A particle performing S.H.M. has velocities of 8 cm/s and 6 cm/s at displacements of 3 cm and 4 cm respectively. Calculate the amplitude and period of S.H.M.
The correct Answer is:Amplitude = 5 cm, T= 3.14 sec
To solve the problem, we will use the formula for the velocity of a particle in Simple Harmonic Motion (SHM):
V=ω√A2−x2
where:
- V is the velocity,
- ω is the angular frequency,
- A is the amplitude,
- x is the displacement.
Given:
1. V1=8cm/s at x1=3cm
2. V2=6cm/s at x2=4cm
Step 1: Write the equations for both velocities
From the first condition:
8=ω√A2−32
8=ω√A2−9(1)
From the second condition:
6=ω√A2−42
6=ω√A2−16(2)
Step 2: Solve for ω from both equations
From equation (1):
ω=8√A2−9
From equation (2):
ω=6√A2−16
Step 3: Set the two expressions for ω equal to each other
8√A2−9=6√A2−16
Step 4: Cross-multiply to eliminate the fractions
8√A2−16=6√A2−9
Step 5: Square both sides to eliminate the square roots
64(A2−16)=36(A2−9)
Step 6: Expand both sides
64A2−1024=36A2−324
Step 7: Rearrange the equation to isolate terms involving A2
64A2−36A2=1024−324
28A2=700
Step 8: Solve for A2
A2=70028=25
A=5cm
Step 9: Find ω using the value of A
Substituting A=5 into either equation for ω. Using equation (1):
ω=8√52−9=8√25−9=8√16=84=2rad/s
Step 10: Calculate the period T
The period T is given by:
T=2πω
T=2π2=πs
Final Answer:
- Amplitude A=5cm
- Period T=πs
- V is the velocity,
- ω is the angular frequency,
- A is the amplitude,
- x is the displacement.
1. V1=8cm/s at x1=3cm
2. V2=6cm/s at x2=4cm
8=ω√A2−32
8=ω√A2−9(1)
6=ω√A2−42
6=ω√A2−16(2)
ω=8√A2−9
ω=6√A2−16
28A2=700
A=5cm
ω=8√52−9=8√25−9=8√16=84=2rad/s
T=2πω
T=2π2=πs
- Amplitude A=5cm
- Period T=πs
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Oscillations (Long Answer ( LA) ( 4 marks Each) )
3 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Superposition of Waves (MCQ’S (1 Mark Each) )
7 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Oscillations (Short Answer I (SA1) ( 2 MARKS Each ) )
6 Videos
- MULTIPLE CHOICE QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MULTIPLE CHOICE QUESTIONSEXERCISE - Communication Systems
6 Videos
- SHORT ANSWER QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SHORT ANSWER QUESTIONSEXERCISE - Assignments
3 Videos
Similar Questions
A particle moving with S.H.M. has velocitiesof 4cm/s and 3cm/s at distances of 3 cm and 4 cm respectively from the equilibrium position. Find
(a)The amplitude of the osciallation
(b) Time period
(c ) The velocity of the particle as is pases through the equilibrium position.
View SolutionA body executing S.H.M. has its velocity 10cm/s and 7cm/s when its displacement from the mean positions are 3cm and 4cm respectively. Calculate the length of the path.
View Solution
Knowledge Check
The velocity of a particle performing S.H.M. are 0.13 m/s and 0.12 m/s. When it is at 0.12 m and 0.13 m from the mean position respectively. Then the amplitude is
A0.117 mB0.177 mC11.7 mD10 mThe acceleration of a particle performing a linear S.H.M. is 16cm/s2, when it is at a dis"tan"ce of 4 cm from the mean position. The period of S.H.M. is
A6.28 secB1.57 secC5 secD3.14 secThe amplitude of particle performing S.H.M. is
AtensorBvectorCscalarDdepending upon magnitude
A particle performing linear S.H.M. has maximum velocity of 25 cm/s and maximum acceleration of 100cm/s2. Find the amplitude and period of oscillation. (π=3.142)
View SolutionA particle is executing linear S.H.M. with a maximum velocity of 50 cm/s and a maximum acceleration of 40 cm/s2. Calculate the amplitude and the period of oscillation.
View SolutionA particle in linear SHM has speeds 4 cm/s and 3 cm/s when its displacements from the mean position are 3 cm and 4 cm , respectively. Find its period of oscillation.
View SolutionThe acceleration of a particle performing a S.H.M. is 0.12m/s2, when the particle is at a dis"tan"ce of 3 cm from its equilibrium position. What is the period of S.H.M. ?
View SolutionTwo blocks of masses 3kg block is attached to a spring with a force constant, kk=900N/ma which is compressed 2m initially from its equilibrium position. When 3kg mass is released, it strikes the 6kg mass and the two stick togther in an inelastic collision.
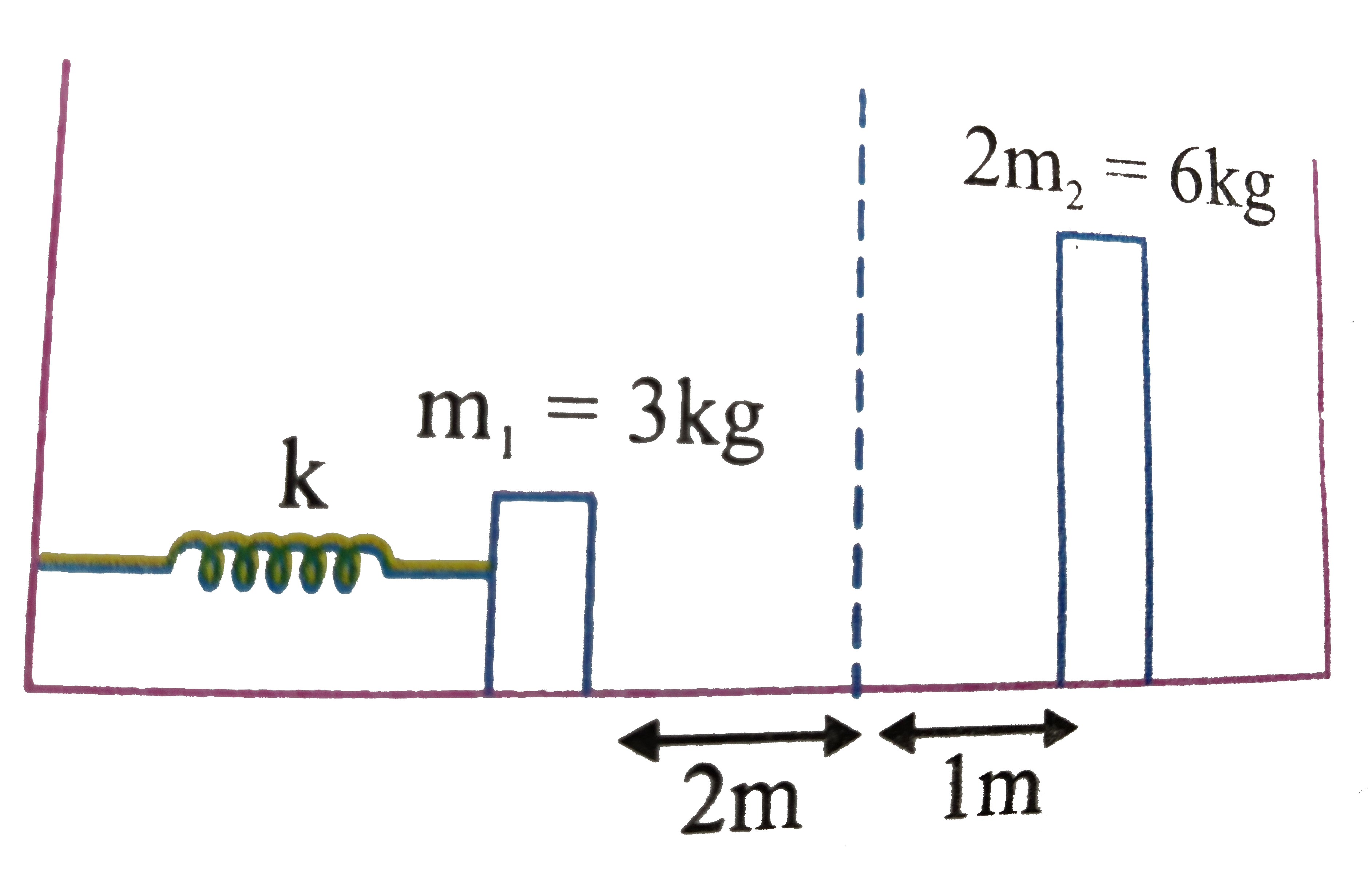
The velocities of a particle executing S.H.M. are 30cm/s and 16cm/s when its displacements are 8cm and 15cm from the equilibrium position. then its amplitude of oscillation in cm is:
View Solution
