Two parallel plate capacitors X and Y have the same area of the plates and same separation between them, are connected in series to a battery of 15 V. X has air between the plates while Y contains a dielectric of constant k = 2.
Calculate the potential difference between the plates of X and Y.
To solve the problem of finding the potential difference between the plates of capacitors X and Y, we will follow these steps:
Step 1: Determine the capacitance of each capacitor
1. Capacitance of capacitor X (CX):
- Since X has air between the plates, its capacitance is given by the formula:
CX=ϵ0Ad
- Let’s denote this capacitance as C.
2. Capacitance of capacitor Y (CY):
- Y contains a dielectric with a constant k=2, so its capacitance is:
CY=k⋅CX=2⋅C=2C
Step 2: Find the equivalent capacitance of the series combination
- For capacitors in series, the equivalent capacitance Ceq is given by:
1Ceq=1CX+1CY
- Substituting the values of CX and CY:
1Ceq=1C+12C
- Finding a common denominator:
1Ceq=22C+12C=32C
- Therefore, the equivalent capacitance is:
Ceq=2C3
Step 3: Calculate the total charge in the circuit
- The total voltage supplied by the battery is V=15V.
- The charge Q on the capacitors can be calculated using:
Q=Ceq⋅V
- Substituting the values:
Q=2C3⋅15=10C
Step 4: Calculate the potential difference across each capacitor
1. Potential difference across capacitor X (VX):
- Using the formula V=QC:
VX=QCX=10CC=10V
2. Potential difference across capacitor Y (VY):
- Similarly, for capacitor Y:
VY=QCY=10C2C=5V
Final Result
- The potential difference between the plates of capacitor X is 10 V and for capacitor Y is 5 V.
1. Capacitance of capacitor X (CX):
- Since X has air between the plates, its capacitance is given by the formula:
CX=ϵ0Ad
- Let’s denote this capacitance as C.
- Y contains a dielectric with a constant k=2, so its capacitance is:
CY=k⋅CX=2⋅C=2C
- For capacitors in series, the equivalent capacitance Ceq is given by:
1Ceq=1CX+1CY
- Substituting the values of CX and CY:
1Ceq=1C+12C
- Finding a common denominator:
1Ceq=22C+12C=32C
- Therefore, the equivalent capacitance is:
Ceq=2C3
- The total voltage supplied by the battery is V=15V.
- The charge Q on the capacitors can be calculated using:
Q=Ceq⋅V
- Substituting the values:
Q=2C3⋅15=10C
1. Potential difference across capacitor X (VX):
- Using the formula V=QC:
VX=QCX=10CC=10V
- Similarly, for capacitor Y:
VY=QCY=10C2C=5V
- The potential difference between the plates of capacitor X is 10 V and for capacitor Y is 5 V.
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Electrostatics (Long Answer ( LA) ( 4 marks Each) )
3 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - CURRENT ELECTRICITY (MCQ’S (1 Mark Each) )
7 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Electrostatics (Short Answer I (SA1) ( 2 MARKS Each ) )
6 Videos
- MULTIPLE CHOICE QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MULTIPLE CHOICE QUESTIONSEXERCISE - Communication Systems
6 Videos
- SHORT ANSWER QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SHORT ANSWER QUESTIONSEXERCISE - Assignments
3 Videos
Similar Questions
Two parallel plate capacitors X and Y have the same area of the plates and same separation between them, are connected in series to a battery of 15 V. X has air between the plates while Y contains a dielectric of constant k = 2.
Calculate the capacitance of each capacitor if equivalent capacitance of the combination is 2 μF
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of εr=4.
Calculate the potential difference between the plates of X and Y.
View Solution
Knowledge Check
A parallel plate capacitor is charged completely and then disconnected from the battery. IF the separation between the plates is reduced by 50% and the space between the plates if filled with a dielectric slab of dielectric constant 10, then the potential difference between the plates
ADecrease by 95%BIncrease by 95%CDecrease by 50%DIncreases by 50%
Two parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of εr=4.
Estimate the ratio of electrostatic energy stored in X and Y .
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same seperation and air between the plates while Y contains a dielectric medium of ∈r=4
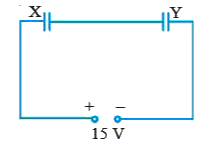
Calculate the potential difference between the plates of X and Y.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of εr=4.
Calculate capacitance of each capacitor if equivalent capacitance of the combination is 4μF.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them.
X has air between the plates while Y contains a dielectric medium of er=4
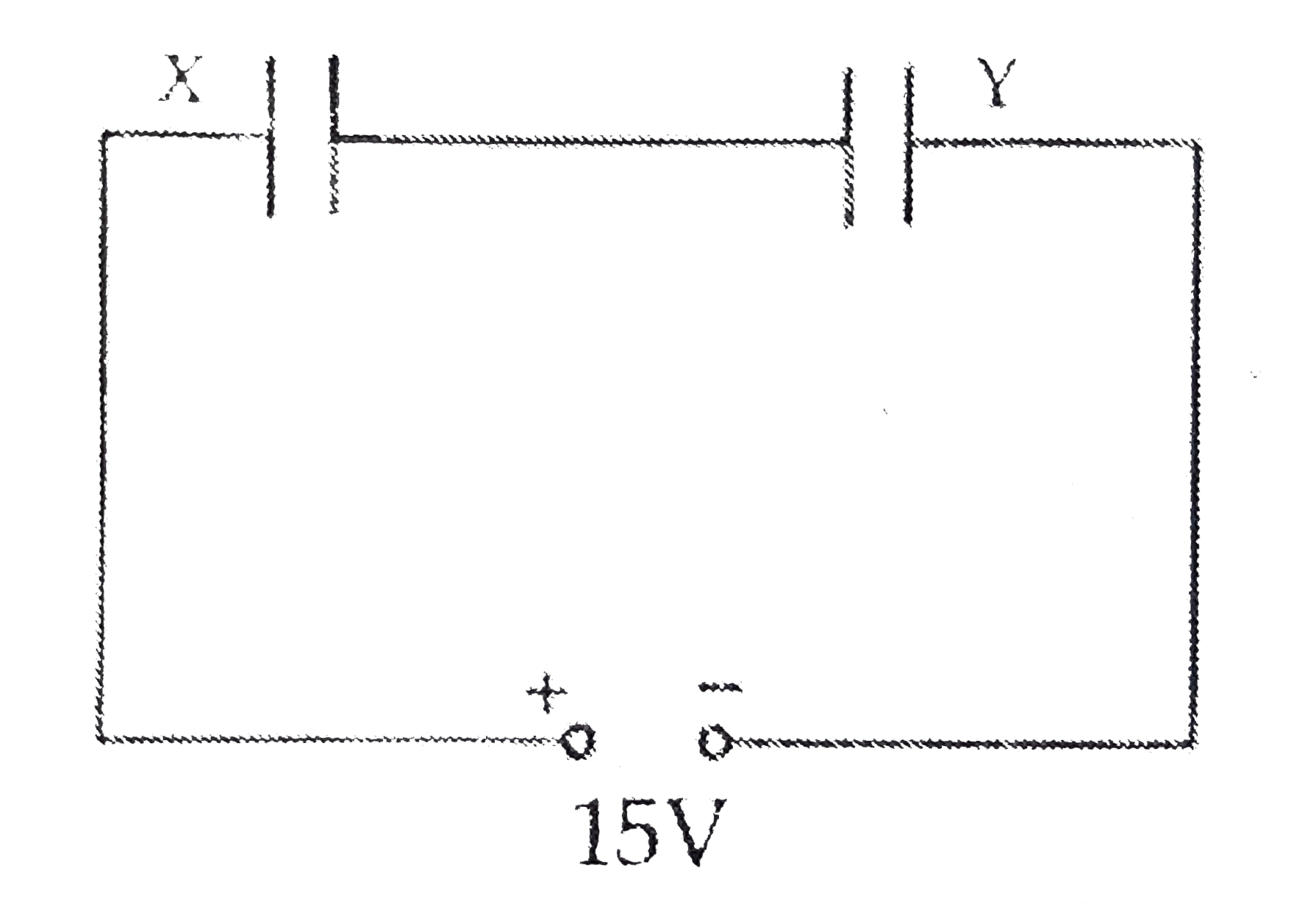
(i) Calculate capacitance of aech capacitor if equivalent capacitance of the combination is 4μF
(ii) Calculate the potential difference between the plates of X and Y
(iii) Estimate the ratio of electrostatic energy stored in X and Y .
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same seperation and air between the plates while Y contains a dielectric medium of ∈r=4

Estimate the ratio of electrostatic energy stored in X and Y.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same seperation and air between the plates while Y contains a dielectric medium of ∈r=4
Calculate capacitance of capacitor if equivalent of the combind system.
View SolutionTwo parallel palate capacitors X and Y have the same area of plates and same separation between then. X has air between the plates and Y contains a dielectric medium of ∈r=4,
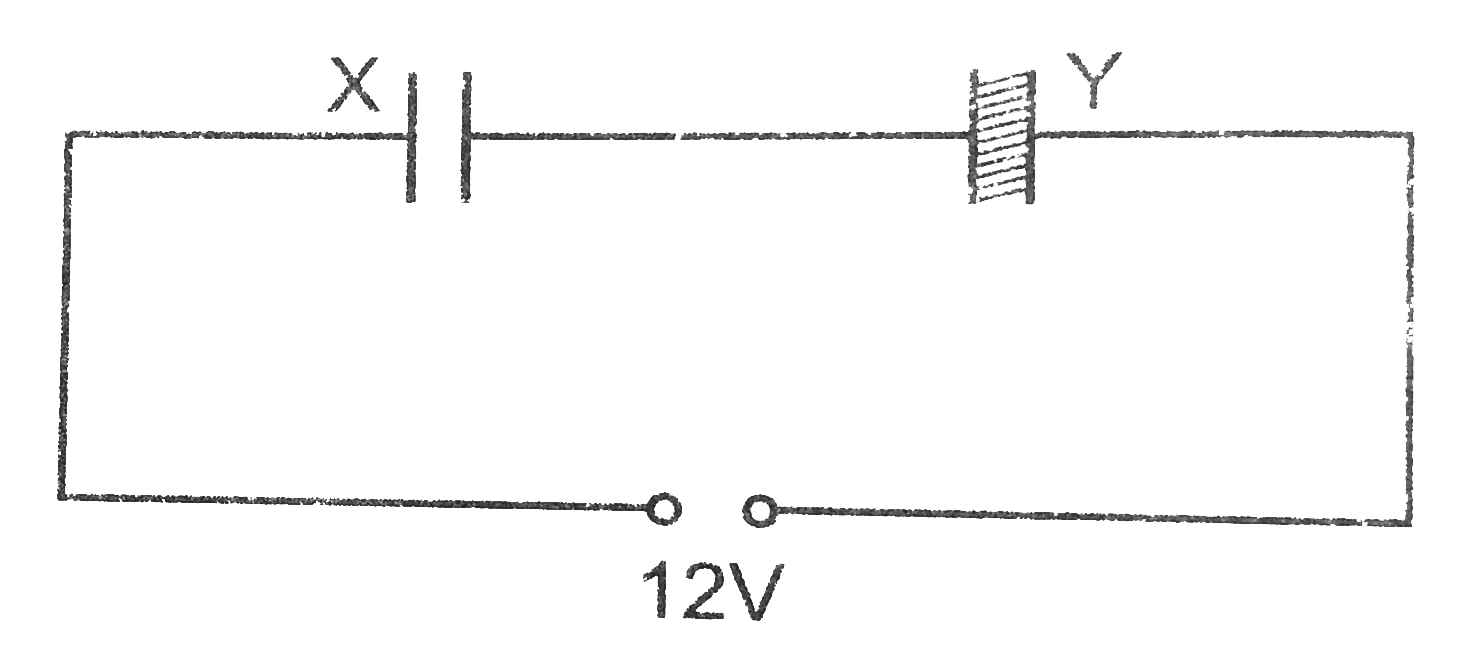
Calculate (i) capacitance of X and Y if equivalent capacitance fo combination is 4μF. (ii) pot diff between the plates of X and Y. (iii) What is the ratio of electrostatic energy stored in X and Y ?
View Solution
