State Kirchhoff’s second (voltage) law.
Step-by-Step Solution:
1. Understanding Kirchhoff’s Second Law: Kirchhoff’s second law, also known as Kirchhoff's Voltage Law (KVL), states that the sum of the electrical potential differences (voltage) around any closed loop in a circuit is equal to zero.
2. Defining a Closed Loop: A closed loop in a circuit is a path that starts and ends at the same point without any breaks. For example, if you have a circuit with a battery and resistors, you can trace a path that returns to the starting point.
3. Applying the Law: When you traverse the loop, you need to account for the potential differences across each component. If you encounter a battery, the voltage is considered positive when moving from the negative terminal to the positive terminal. Conversely, if you move from the positive terminal to the negative terminal, the voltage is considered negative.
4. Sign Convention: The sign convention is crucial in applying KVL. If the direction of current flow is the same as the direction you are moving in the loop, the potential drop across a resistor is taken as negative. If you are moving against the current, the potential drop is positive.
5. Example Calculation: For instance, if you have a battery of 5V and a resistor of 5Ω in the loop:
- The potential difference across the battery is +5V (moving from - to +).
- The potential difference across the resistor (with a current of 1A flowing through it) is -5V (since the direction of current and the direction of movement are the same).
- According to KVL: +5V (from the battery) - 5V (across the resistor) = 0V.
6. Conclusion: Therefore, the sum of the potential differences in the closed loop is zero, confirming Kirchhoff's Voltage Law.
---
- The potential difference across the battery is +5V (moving from - to +).
- The potential difference across the resistor (with a current of 1A flowing through it) is -5V (since the direction of current and the direction of movement are the same).
- According to KVL: +5V (from the battery) - 5V (across the resistor) = 0V.
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - CURRENT ELECTRICITY (Short Answer I (SA1) ( 2 MARKS Each ) )
8 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - CURRENT ELECTRICITY ( Short Answer II (SA2) ( 3 MARKS Each ) )
7 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - CURRENT ELECTRICITY (MCQ’S (1 Mark Each) )
7 Videos
- MULTIPLE CHOICE QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MULTIPLE CHOICE QUESTIONSEXERCISE - Communication Systems
6 Videos
- SHORT ANSWER QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SHORT ANSWER QUESTIONSEXERCISE - Assignments
3 Videos
Similar Questions
Knowledge Check
Kirchhoff's second law is based on law of conservation of
Asum of mass and energyBmomentumCenergyDchargeAssertion:- Kirchhoff's voltage law indicates that field is conservative.
Reason:- Potential difference between two points in a circuit does not depend on pathAIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are False.Kirchhoff's voltage law is based on the law of conservation of
AmomentumBchargeCmassDenergy
What are the basis of Kirchhoff's current law and voltage law ?
View SolutionState Kirchhoff' voltage law
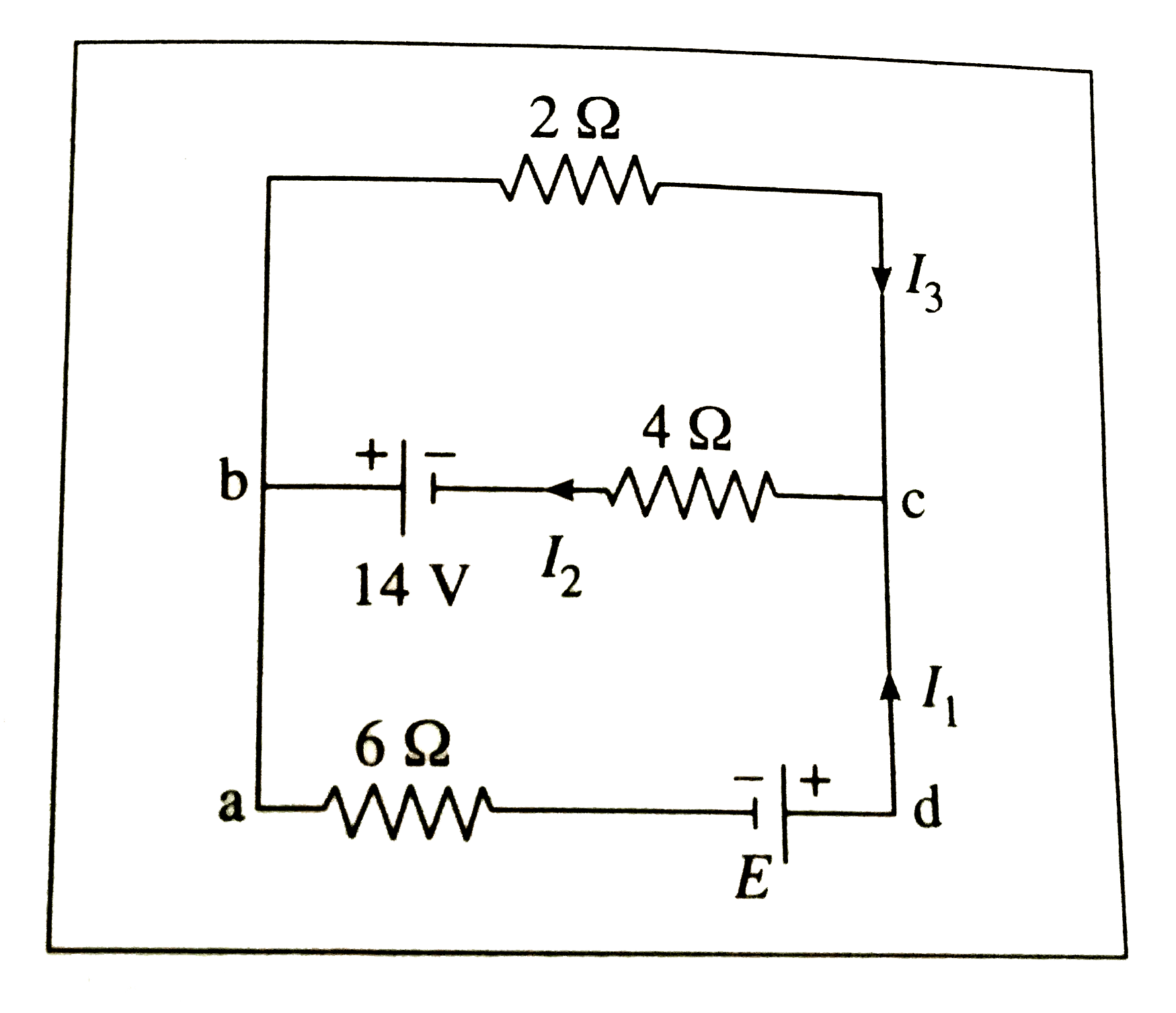
View SolutionIn the given circuit, apply Kirchhoff's voltage law to loop abcda, and write the corresponding equation.
View SolutionThe Kirchhoff's Current Law|The Kirchhoff's Voltage Law
View SolutionState the two Kirchhoff's laws.
View Solution