The magnetic flux through a loop varries according to the relation ∅ = 8t2+6t+2,∅ is in milliweber and t is in second. What is the magnitude of the induced emf in the loop
at t = 2 seconds?
To find the magnitude of the induced emf in the loop at t=2 seconds, we will follow these steps:
Step 1: Understand the relationship between magnetic flux and induced emf
The induced emf (E) in a loop is given by Faraday's law of electromagnetic induction, which states:
E=−dΦdt
where Φ is the magnetic flux.
Step 2: Differentiate the magnetic flux function
Given the magnetic flux Φ(t)=8t2+6t+2 (in milliwebers), we need to differentiate this function with respect to time t:
dΦdt=ddt(8t2+6t+2)
Using the power rule of differentiation:
dΦdt=16t+6
Step 3: Substitute t=2 seconds into the derivative
Now, we will substitute t=2 seconds into the differentiated function to find the induced emf:
dΦdt∣∣∣t=2=16(2)+6
Calculating this gives:
dΦdt∣∣∣t=2=32+6=38 milliwebers/second
Step 4: Calculate the induced emf
According to Faraday's law, the induced emf is:
E=−dΦdt
Since we are interested in the magnitude, we take the absolute value:
E=38 milliwebers/second
Step 5: Convert milliwebers to volts
Since 1 milliweber corresponds to 1 milliVolt when considering induced emf, we can express this as:
E=38 milliVolts=38×10−3 Volts=0.038 Volts
Final Answer
Thus, the magnitude of the induced emf in the loop at t=2 seconds is:
E=0.038 Volts
---
The induced emf (E) in a loop is given by Faraday's law of electromagnetic induction, which states:
E=−dΦdt
where Φ is the magnetic flux.
Given the magnetic flux Φ(t)=8t2+6t+2 (in milliwebers), we need to differentiate this function with respect to time t:
dΦdt=ddt(8t2+6t+2)
Using the power rule of differentiation:
dΦdt=16t+6
Now, we will substitute t=2 seconds into the differentiated function to find the induced emf:
dΦdt∣∣∣t=2=16(2)+6
Calculating this gives:
dΦdt∣∣∣t=2=32+6=38 milliwebers/second
According to Faraday's law, the induced emf is:
E=−dΦdt
Since we are interested in the magnitude, we take the absolute value:
E=38 milliwebers/second
Since 1 milliweber corresponds to 1 milliVolt when considering induced emf, we can express this as:
E=38 milliVolts=38×10−3 Volts=0.038 Volts
Thus, the magnitude of the induced emf in the loop at t=2 seconds is:
E=0.038 Volts
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Electromagnetic Induction ( Short Answer II (SA2) ( 3 MARKS Each ) )
5 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Electromagnetic Induction (Long Answer ( LA) ( 4 marks Each) )
2 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Electromagnetic Induction (Very Short Answer (VSA) ( 1 MARK Each ) )
7 Videos
- MULTIPLE CHOICE QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MULTIPLE CHOICE QUESTIONSEXERCISE - Communication Systems
6 Videos
- SHORT ANSWER QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SHORT ANSWER QUESTIONSEXERCISE - Assignments
3 Videos
Similar Questions
The magnetic flux through a loop varries according to the relation ∅ = 8t2+6t+2,∅ is in milliweber and t is in second. What is the magnitude of the induced emf in the loop
at t = 2 seconds?
View SolutionThe magnetic flux through a loop is varying according to relation ϕ=6t2+7t+1 where ϕ is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second ?
View Solution
Knowledge Check
The magnetic flux (ϕ) in a closed circuit of resistance 20Ω varies with time (t) according to the equation ϕ=7t2−4t where ϕ is in weber and t is in seconds. The magnitude of the induced current at t =0.25s is
A25mAB0.025mAC47 mAD175 mA
The magnetic flux thropugh a loop varies according to the relation ϕ=t2+6t+C, where 'C' is constant, ϕ is in milliwebe3r and 't' is in sedcond. What is the mognitude of induced e.m.f. in the loop at t = 2 seconds ?
View SolutionThe magnetic flux through a loop is varying according to relation ϕ=6t2+7t+1 where ϕ is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second ?
View SolutionThe magnetic flux passing perpendicular to the plane of the coil and directed into the paper is varying according to the relation ϕ=3t2+2t+3, where ϕ is in milliweber and t is in second. Then the magnitude of emf induced in the loop when t=2 second is-

View SolutionIn Fig. 30-60, the magnetic flux through the loop increases according to the relation ϕB=3.0t2=7.0t, where ϕB is in milliwebers and tis in seconds. (a) What is the magnitude of the emf induced in the loop when t = 1.5 s? (b) Is the direction of the current through R to the right or left?

View SolutionThe mangnetic flux passsing perpendicular to the plane of a coil and directed into the paper is given by ϕ=5t2+6t+2 where ϕ is in milliwebers and t in seconds.
(a) What is the magnitude of the induced emf set up in the loop at t=1s?
(b) What is the direction of current through the resistor R ?
View SolutionIn the given figure the magnetic flux through the loop increases according to the relation
ϕB(t)=10t2+20t, where ϕB is in milliwebers and t is in seconds.
The magnitude of current throught R=2Ω resistor at t=5 s is _______ mA.
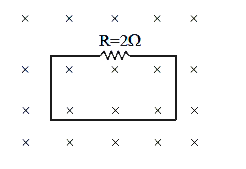
View SolutionThe magnetic flux passing prependicular to the plane of the coil directed into the paper is varying according to the relation
ϕ=6t2+8t+I0 , where ϕ is in weber and t in second.
(a) What is the magnitude of emf induced in the loop when t=2sec ?
(b) What is the magnitude and direction of current at t=2sec ?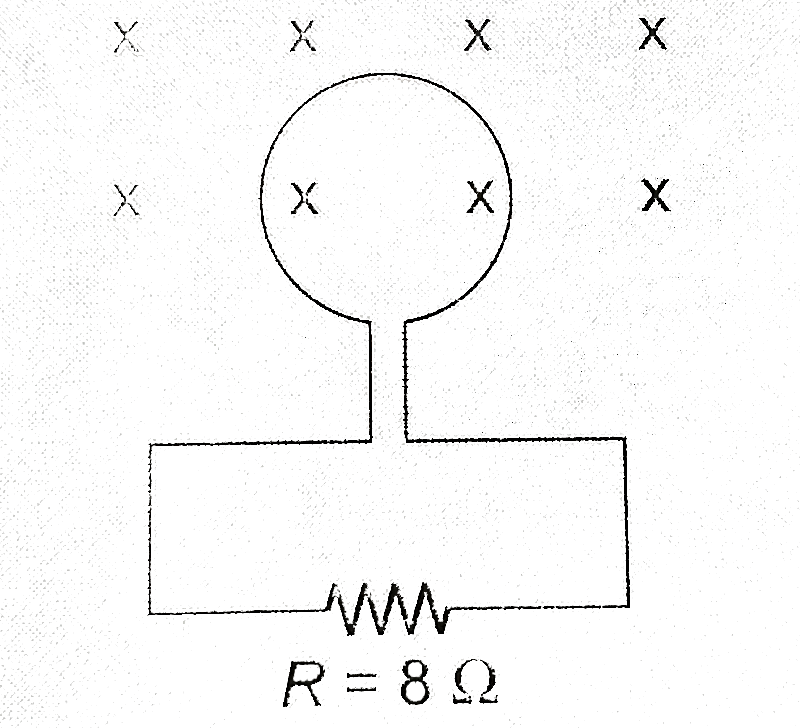
View Solution
