The regression equation of y on x is 2x-5y +60 =0.
Mean of x = 18
∴¯y=□
σx:σy=3:2
∴byx=□□
∴r=□
The correct Answer is:18,19,2,250.6
To solve the problem step by step, we will follow the information provided in the question and the video transcript.
Step 1: Identify the regression equation
The regression equation of y on x is given as:
2x−5y+60=0
Step 2: Find the mean of y using the mean of x
We know that the mean of x (denoted as ¯x) is 18. We can substitute this value into the regression equation to find the mean of y (denoted as ¯y).
Substituting ¯x=18 into the regression equation:
2(18)−5¯y+60=0
Calculating this gives:
36−5¯y+60=096−5¯y=05¯y=96¯y=965=19.2
Step 3: Find the slope of the regression line byx
The regression equation can be rearranged to express y in terms of x:
5y=2x+60y=25x+12
From this, we can see that the slope byx is:
byx=25
Step 4: Determine the ratio of standard deviations σx:σy
We are given that:
σx:σy=3:2
This implies:
σxσy=32orσyσx=23
Step 5: Find the correlation coefficient r
The relationship between the slope byx and the correlation coefficient r is given by:
byx=r⋅σyσx
Substituting the known values:
25=r⋅23
To find r, we rearrange this equation:
r=25⋅32
Calculating this gives:
r=35=0.6
Final Answers
- ¯y=19.2
- byx=25
- r=0.6
The regression equation of y on x is given as:
2x−5y+60=0
We know that the mean of x (denoted as ¯x) is 18. We can substitute this value into the regression equation to find the mean of y (denoted as ¯y).
2(18)−5¯y+60=0
Calculating this gives:
36−5¯y+60=096−5¯y=05¯y=96¯y=965=19.2
The regression equation can be rearranged to express y in terms of x:
5y=2x+60y=25x+12
From this, we can see that the slope byx is:
byx=25
We are given that:
σx:σy=3:2
This implies:
σxσy=32orσyσx=23
The relationship between the slope byx and the correlation coefficient r is given by:
byx=r⋅σyσx
Substituting the known values:
25=r⋅23
To find r, we rearrange this equation:
r=25⋅32
Calculating this gives:
r=35=0.6
- ¯y=19.2
- byx=25
- r=0.6
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 4. TIME SERIES (I) Choose the correct alternative.)5videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 4. TIME SERIES (II) Fill in the blanks5videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 3. LINEAR REGRESSION (IV.Answer the following:)15videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS9videos
PROBABILITY DISTRIBUTION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS8videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
If r = 0.5, σx=3,σ2y=16 then byx =…
A0.375B0.667C2.667D0.093 - Question 2 - Select One
The area bounded by the lines x=0,y=0,x+y=1,2x+3y=6 (in square units ) is
A2B213C212D3
If the regression equations are 8x–10y+66=0 and 40x–18y=214, the mean value of y is…..
View SolutionMean of x= 25
Mean of y =20
σx=4
σy=3
r=0.5
byx=□
bxy=□
When x = 10
y−□=□(10−□)
∴y=□View SolutionSquare of 3x – 4y is
View SolutionMean of x= 53
Mean of y = 28
Regression coefficient of y on x = - 1.2
Regression coefficient of x on y= - 0.3
When x = 50 ,
y−□=□(50−□)
∴y=□View SolutionMean of x= 53
Mean of y = 28
Regression coefficient of y on x = - 1.2
Regression coefficient of x on y= - 0.3
When y = 25
x−□=□(25−□)
∴x=□View Solution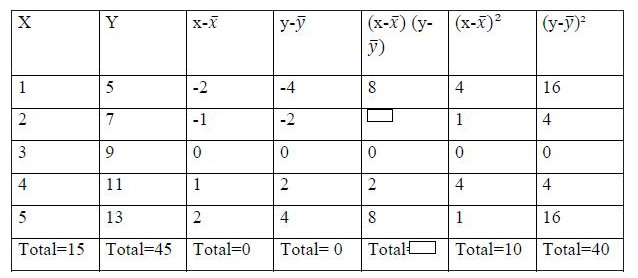
Mean of x=¯x=□
Mean y=¯y=□
bxy=□□
byx=□□
Regression equation of x on y is x−¯x=bxy(y−¯y)
∴ Regression equation of x on y is □
Regression equation of y on x is y−¯y=byx(x−¯x)
∴ Regression equation of y on x is □View Solution

