By spending almost ₹ 250 ,Rakhi bought some kg grapes(x) & some dozens of bananas(y), then as a constraint this information can be expressed by_______
The correct Answer is:x+y<250
To express the information given in the question as a constraint, we can follow these steps:
1. Define Variables:
- Let x be the amount of money spent on grapes (in rupees).
- Let y be the amount of money spent on bananas (in rupees).
2. Understand the Total Spending:
- According to the problem, Rakhi spent almost ₹250 on grapes and bananas combined.
3. Express the Total Spending:
- The total amount spent on grapes and bananas can be expressed as x+y.
4. Set Up the Constraint:
- Since Rakhi spent almost ₹250, this means that the total spending x+y must be less than ₹250.
- Therefore, we can write the constraint as:
x+y<250
Final Expression:
The constraint that expresses the information given in the question is:
x+y<250
---
- Let x be the amount of money spent on grapes (in rupees).
- Let y be the amount of money spent on bananas (in rupees).
- According to the problem, Rakhi spent almost ₹250 on grapes and bananas combined.
- The total amount spent on grapes and bananas can be expressed as x+y.
- Since Rakhi spent almost ₹250, this means that the total spending x+y must be less than ₹250.
- Therefore, we can write the constraint as:
x+y<250
The constraint that expresses the information given in the question is:
x+y<250
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II LINEAR PROGRAMMING PROBLEMS (D. Solve the following problems)12videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II LINEAR PROGRAMMING PROBLEMS (E. Activities)3videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II LINEAR PROGRAMMING PROBLEMS (B. State whether each of the following statement is TRUE or FALSE)12videos
QUESTION BANK 2021
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS9videos
PROBABILITY DISTRIBUTION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS8videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Ganesh owns a godown used to store electronic gadgets like refrigerator(x) & microwave(y),If the godown can accommodate at most 75 gadgets, then this can be expressed as a constraint by ________________
View SolutionOne of the important application of the differential equation is to find out the family of curves for which some conditions involving the derivatives are given. For this one can proceed by making use of the following facts. Equation of the tangent at a point (x, y) to the curve y=f(x) is given by Y−y=dydx(X−x). At the X-axis, Y = 0, and X=x−ydydx At the Y-axis, X = 0, and Y=y−dydx. Similar things, can be obtained for normals by writing its equation as (Y−y)dydx+X−x=0.If y=f(x) be a curve such questions length of x intercept of tangent is equal to the distance of the point of tangency from x-axis f(x) is given by
View Solution
Knowledge Check
- Question 1 - Select One
At infinite dilution, when the dissociation of electrolyte is complete, each ion makes a definite contribution towards the molar conductance of electrolyte, irrespective of the nature of the other ion with which it is associated.
the molar conductance of an electrolyte at infinite dilution can be expressed as the sum of the contributions from its individual ions.
AxBy→xAy++yBx−
Λ∘m(AxBy)=xλ∘Ay++yλ∘Bx−
where, x and y are the number of cations and anions respectively.
The degree of ionisation 'α' of weak electrolyte can be calculated as :
α=ΛmΛ∘m
The molar conductance of 0.001 M acetic acid is 50ohm−2cm2mol−1. The maximum value of molar conductance of acetic acid is 250ohm−1cm2mol−1. What is the degree of dissociation (α) of acetic acid ?A0.5B0.2C0.3D0.4 - Question 2 - Select One
Read the given table stating some features of molecules X and Y.

Here, the X and Y can be identified asAX−rRNA,Y=tRNABX−mRNA,Y−tRNACX−mRNA,Y−rRNADX−tRNA,Y−tRNA - Question 3 - Select One
Whenever the terms on the two sides of the equation are of different nature, then equations are known as Non standard form, some of them are in the form of an ordinary equation but can not be solved by standard procedures.
Now standard problems require high degree of logic, they also require the use of graphs, inverse properties of functions, inequalities.
On the basis of above information, answer the following questions:
The equation 2cos2(x2)=x2+x−2,0<x−2,0<x≤π2 hasAone real solutionsBmore than one real solutionsCno real solutionsDnone of the above
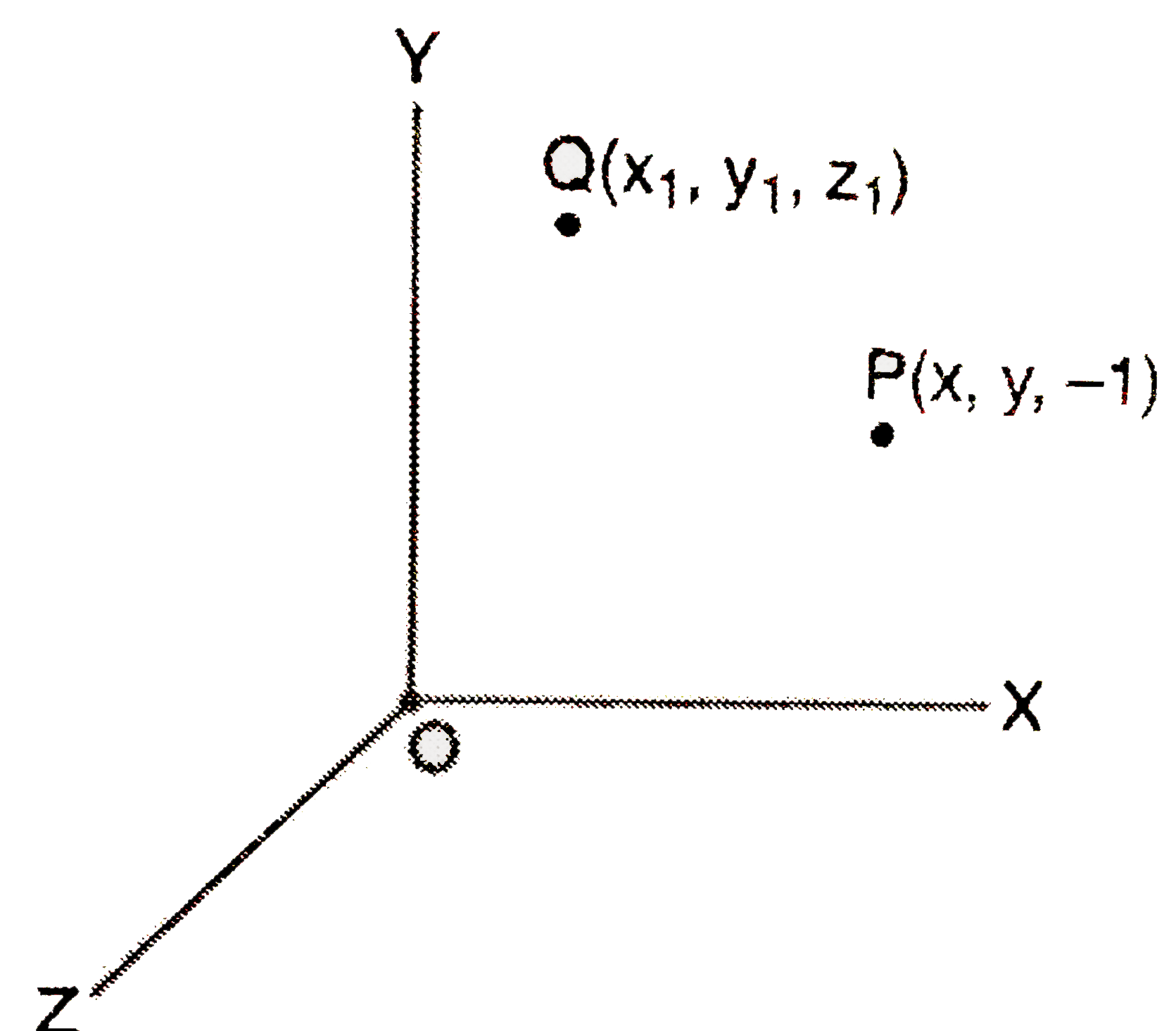
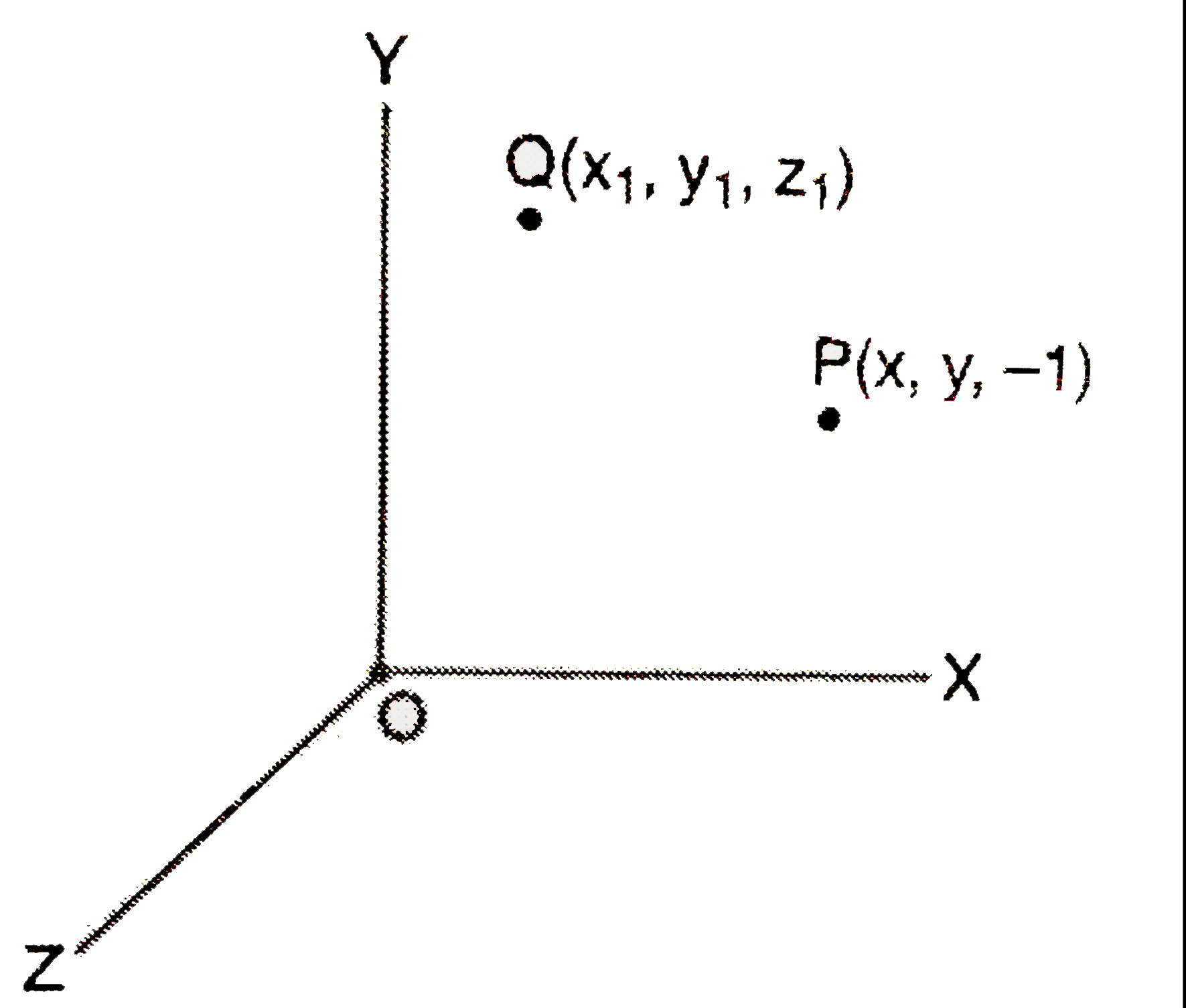
Sppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are

Answer the following questions.
At Q torque acting on the mass can be expressed as :View SolutionSppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are
Answer the following questions.
Coordinates of P are :View SolutionSppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are
Answer the following questions.
Work done the for the motion of the points mass from P to Q is :View SolutionTO reprsent word problem in the form of quadratic equations, suppose the unknown required quantity can be taken as some variable x (say) and express the given condition in the form of x to form an equaiton in x. Then wew express the equation in the descending powers of x. Thus standard quadratic equations is ax2+bx+c=0,a≠0.
Sandeep's father is 30 years older than him. The product of their ages 2 years from now will be 400. To find Sandeep's present age, the equation isView SolutionWhenever the terms on the two sides of the equation are of different nature, then equations are known as Non standard form, some of them are in the form of an ordinary equation but can not be solved by standard procedures.
Now standard problems require high degree of logic, they also require the use of graphs, inverse properties of functions, inequalities.
On the basis of above information, answer the following questions:
The number of real solutions of the equation sin(ex)=5x+5−x isView Solution

