Find the feasible solutions of in equations 3x+2y≤18,2x+y≤10,X≥0Y≥0
The correct Answer is:z has a minimum value 22.5 when x=2,y=0.5
To find the feasible solutions of the inequalities 3x+2y≤18, 2x+y≤10, x≥0, and y≥0, we will follow these steps:
Step 1: Rewrite the inequalities
We have the following inequalities:
1. 3x+2y≤18
2. 2x+y≤10
3. x≥0
4. y≥0
Step 2: Find the intercepts of the first inequality
For the inequality 3x+2y≤18:
- To find the x-intercept, set y=0:
3x+2(0)=18⟹3x=18⟹x=6
- To find the y-intercept, set x=0:
3(0)+2y=18⟹2y=18⟹y=9
Step 3: Find the intercepts of the second inequality
For the inequality 2x+y≤10:
- To find the x-intercept, set y=0:
2x+0=10⟹2x=10⟹x=5
- To find the y-intercept, set x=0:
2(0)+y=10⟹y=10
Step 4: Graph the inequalities
1. Graph the line 3x+2y=18:
- Plot the points (6, 0) and (0, 9).
- Shade the area below this line.
2. Graph the line 2x+y=10:
- Plot the points (5, 0) and (0, 10).
- Shade the area below this line.
3. Include the axes:
- Since x≥0 and y≥0, only the first quadrant is considered.
Step 5: Identify the feasible region
The feasible region is where the shaded areas of both inequalities overlap in the first quadrant. This region will be bounded by the lines and the axes.
Step 6: Determine the vertices of the feasible region
To find the vertices of the feasible region, we need to find the points of intersection of the lines:
1. Solve the equations 3x+2y=18 and 2x+y=10 simultaneously.
From 2x+y=10, we can express y in terms of x:
y=10−2x
Substituting this into the first equation:
3x+2(10−2x)=18
3x+20−4x=18
−x+20=18
−x=−2⟹x=2
Now substitute x=2 back into y=10−2x:
y=10−2(2)=10−4=6
So one vertex is (2,6).
Step 7: Check other vertices
- The vertices from the intercepts are:
- (6,0)
- (0,9)
- (5,0)
- (0,10)
- (2,6)
Conclusion
The feasible region is bounded by the points (0,0), (2,6), (5,0), and (0,9).
We have the following inequalities:
1. 3x+2y≤18
2. 2x+y≤10
3. x≥0
4. y≥0
For the inequality 3x+2y≤18:
- To find the x-intercept, set y=0:
3x+2(0)=18⟹3x=18⟹x=6
- To find the y-intercept, set x=0:
3(0)+2y=18⟹2y=18⟹y=9
For the inequality 2x+y≤10:
- To find the x-intercept, set y=0:
2x+0=10⟹2x=10⟹x=5
- To find the y-intercept, set x=0:
2(0)+y=10⟹y=10
1. Graph the line 3x+2y=18:
- Plot the points (6, 0) and (0, 9).
- Shade the area below this line.
- Plot the points (5, 0) and (0, 10).
- Shade the area below this line.
- Since x≥0 and y≥0, only the first quadrant is considered.
The feasible region is where the shaded areas of both inequalities overlap in the first quadrant. This region will be bounded by the lines and the axes.
To find the vertices of the feasible region, we need to find the points of intersection of the lines:
1. Solve the equations 3x+2y=18 and 2x+y=10 simultaneously.
y=10−2x
3x+2(10−2x)=18
3x+20−4x=18
−x+20=18
−x=−2⟹x=2
y=10−2(2)=10−4=6
- The vertices from the intercepts are:
- (6,0)
- (0,9)
- (5,0)
- (0,10)
- (2,6)
The feasible region is bounded by the points (0,0), (2,6), (5,0), and (0,9).
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - DIFFERENTIATION
42 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - APPLICATIONS OF DERIVATIVE
44 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - LINE AND PLANE
40 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Find the feasible solution of linear inequations 2x+3y≤12,2x+y≤8,x≥0,y≥0 by graphically
View Solution(a) Draw the feasible region of inequation:
x+y≤4,x≥0,y≥0
(b) Draw the graph of the following LPP:
3x+y≤17,x,y≥0
(c) Shade the feasible region of LLP:
(i) x+3y≥3,x+y≥2,x≥0,y≥0
(ii) x+2y≤8,3x+2y≤12,x≥0,y≥0
View Solution
Knowledge Check
The Corner points of feasible region for the inequations , x+y≤5,x+2y≤6,x≥0,y≥0 are
A(0,3),(5,0),(0,5),(6,0)B(0,3),(5,0),(4,1),(0,0)C(0,0),(1,4),(5,0),(0,3)D(3,0),(0,5)(0,0),(4,1)The graphical solution of the inequalities x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0 is
A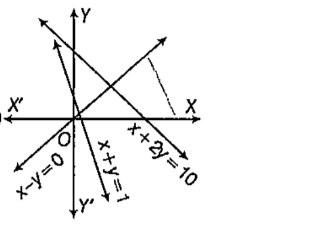 B
B C
C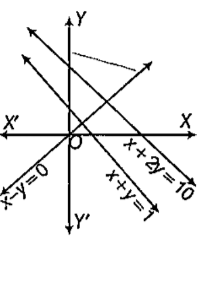 D
D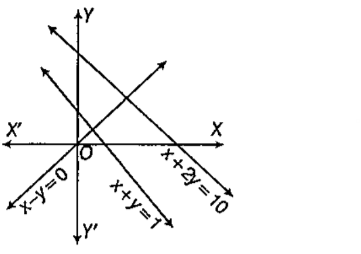
the corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
A(2,0),(2019,4519),(0,3)B(0,3),(2019,4519),(0,5)C(2,0),(2019,4519),(5,0)D(0,0),(2,0),(2019,4519),(0,3)
x+y≥24,2x+y≥32,x≥0,y≥0
View SolutionFind the graphical solutions for the system of linear inequations 2x+y≤2,x−y≤1
View Solution3x+4y≤18,2x+3y≥3andx,y≥0 is
View SolutionThe feasible region of a LPP under the constraints x−y≤1,x+y≥3,x≥0,y≥0
View SolutionThe solution set of
x−2y≥0,2x−y≤−2,x≥0,y≥0 is
View Solution
