Find the mean and variance of the number randomly selected from 1 to 15.
To find the mean and variance of a number randomly selected from 1 to 15, we can follow these steps:
Step 1: Identify the Random Variable
The random variable X can take any value from the set {1,2,3,…,15}.
Step 2: Determine the Probability
Since the selection is random and each number has an equal chance of being selected, the probability P(X=i) for each i (where i is any number from 1 to 15) is:
P(X=i)=115for i=1,2,…,15
Step 3: Calculate the Mean (Expected Value)
The mean (or expected value) E(X) is calculated using the formula:
E(X)=15∑i=1i⋅P(X=i)
Substituting the probabilities:
E(X)=15∑i=1i⋅115=11515∑i=1i
The sum of the first n natural numbers is given by:
n∑i=1i=n(n+1)2
For n=15:
15∑i=1i=15(15+1)2=15×162=120
Thus, substituting back into the expected value:
E(X)=115⋅120=8
Step 4: Calculate the Variance
The variance Var(X) is calculated using the formula:
Var(X)=E(X2)−(E(X))2
First, we need to calculate E(X2):
E(X2)=15∑i=1i2⋅P(X=i)=11515∑i=1i2
The sum of the squares of the first n natural numbers is given by:
n∑i=1i2=n(n+1)(2n+1)6
For n=15:
15∑i=1i2=15(15+1)(2⋅15+1)6=15⋅16⋅316=1240
Now substituting back into the expected value of X2:
E(X2)=115⋅1240=124015=2483
Now, we can calculate the variance:
Var(X)=E(X2)−(E(X))2=2483−82=2483−64
Converting 64 to a fraction with a denominator of 3:
64=1923
Thus:
Var(X)=2483−1923=563
Final Results
- Mean E(X)=8
- Variance Var(X)=563
The random variable X can take any value from the set {1,2,3,…,15}.
Since the selection is random and each number has an equal chance of being selected, the probability P(X=i) for each i (where i is any number from 1 to 15) is:
P(X=i)=115for i=1,2,…,15
The mean (or expected value) E(X) is calculated using the formula:
E(X)=15∑i=1i⋅P(X=i)
Substituting the probabilities:
E(X)=15∑i=1i⋅115=11515∑i=1i
The sum of the first n natural numbers is given by:
n∑i=1i=n(n+1)2
For n=15:
15∑i=1i=15(15+1)2=15×162=120
Thus, substituting back into the expected value:
E(X)=115⋅120=8
The variance Var(X) is calculated using the formula:
Var(X)=E(X2)−(E(X))2
First, we need to calculate E(X2):
E(X2)=15∑i=1i2⋅P(X=i)=11515∑i=1i2
The sum of the squares of the first n natural numbers is given by:
n∑i=1i2=n(n+1)(2n+1)6
For n=15:
15∑i=1i2=15(15+1)(2⋅15+1)6=15⋅16⋅316=1240
Now substituting back into the expected value of X2:
E(X2)=115⋅1240=124015=2483
Var(X)=E(X2)−(E(X))2=2483−82=2483−64
Converting 64 to a fraction with a denominator of 3:
64=1923
Thus:
Var(X)=2483−1923=563
- Mean E(X)=8
- Variance Var(X)=563
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - BINOMIAL DISTRIBUTION
20 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - DIFFERENTIAL EQUATIONS
38 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
A die is thrown 6 times. Find the mean and variance of the number of aces.
View SolutionAn unbiased coin is tossed 4 times. Find the mean and variance of the number of heads obtained.
View SolutionFind the mean and variance for each of the data :
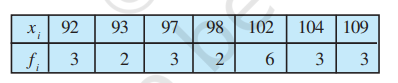
View SolutionFind the mean and variance for each of the data :

View SolutionFind the mean and variance of the numbers obtained on a throw of an unbiased die.
View SolutionFind the mean and variance of the number of heads when two coins are tossed simultaneously.
View SolutionFind the mean and variance of the number of heads in the two tosses of a coin.
View SolutionFind the mean and variance of the number of tails when three coins are tossed simultaneously.
View SolutionTwo cards are drawn from a well shuffled pack of 52 cards. Find the mean and variance for the number of face cards obtained.
View SolutionFind the mean and variance of first 10 multiples of 3.
View Solution
