Prove that the measure of the angle between two main diagonals of a cube is cos−113.Solution in Odia
Step by step video & image solution for Prove that the measure of the angle between two main diagonals of a cube is cos^(-1)frac[1][3]. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A R is a relation on set A such that R=R−1, then write the type of the relation R.
04:23View SolutionLet Х and У be the sets containing m and n elements respectively. How many one-one functions аre there from Х to У.
06:31View SolutionProve that the acute angle between two diagonals of a cube is cos^(-1)((1)/(3))
04:18View SolutionShow that the angle between two diagonals of a cube is cos−1(13).
08:06View Solutionसिद्ध कीजिए की घन के विकर्णों के बीच का कोण cos−(13) होता है ।
04:59View SolutionShow that the angle between any two diagonals of a cube is cos−1(13).
03:41View SolutionProve that the smaller angle between any two diagonals of a cube is cos−113.
05:17View Solutionसिद्ध कीजिए कि एक घन के विकर्णों के बीच का कोण cos−1(13) या tan−12√2 होता है ।
06:18View SolutionProve that the acute angle between two diagonals of a cube is cos−1(13).
03:36View SolutionShow that the angle between two diagonals of a cube is cos−1(13).
05:41View SolutionShow that the angle between the diagonal of a cube is cos−1(13).
08:03View SolutionConsider a cube of side 'a' unit has one vertex at the origin O.
Show that the angle between the main diagonals of the above cube is cos−1(13)
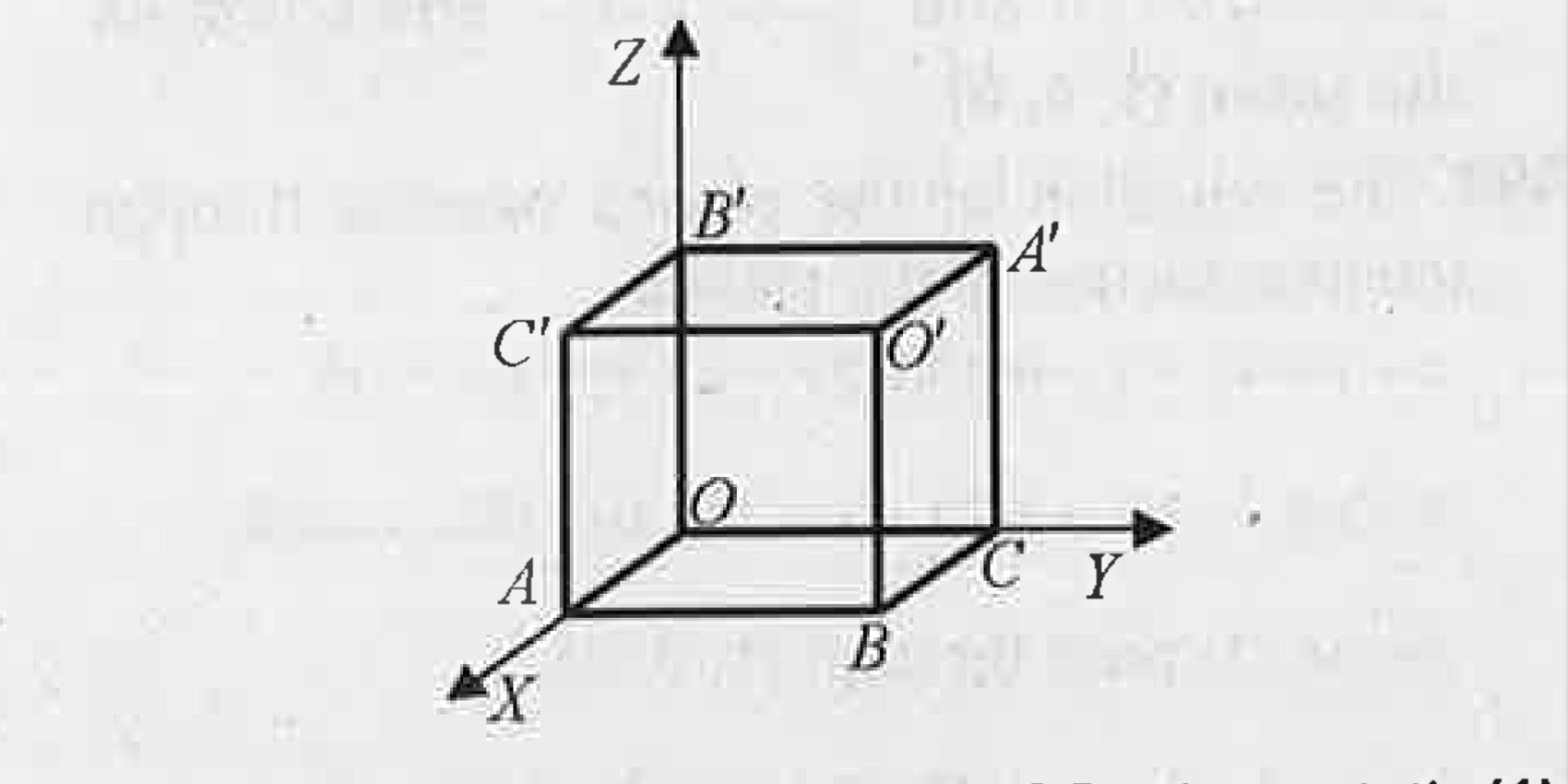 08:27View Solution
08:27View SolutionProve that the measure of the angle between two main diagonals of a cube is cos−113.
03:44View SolutionProve the following by vector method. Measure of the angle between two diagonals of a cube is cos−1(13)
08:03View SolutionProve the angle between the diagonal of one of the faces of the cube and the diagonal of the cube intersecting the diagonal of the face of the cube is cos−1√23
03:44View SolutionProve that the measure of the angle between two main diagonals of a cube is cos−113.
08:03View Solution

